
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Фибоначчи
|
|
|
|
Идея метода.
Отличается от метода золотого сечения величиной коэффициента λ в формулах (8) или (9), определяющих длины отрезков поиска  k =
k =  k (λ), k = 0,1,2,…. Сама схема остается прежней.
k (λ), k = 0,1,2,…. Сама схема остается прежней.
Изменив коэффициент λ, причем выбирая 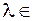 (1/2, 1), можно получить другую последовательность {
(1/2, 1), можно получить другую последовательность {  k (λ)}, и, следовательно, иной способ выбора промежуточных точек yk, zk.
k (λ)}, и, следовательно, иной способ выбора промежуточных точек yk, zk.
Лемма 3. Пусть 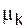 = Fk–1/Fk, k = 2,3,…. Тогда справедливы свойства:
= Fk–1/Fk, k = 2,3,…. Тогда справедливы свойства:
1) 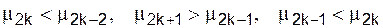 ;
;
2) 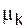 →
→ 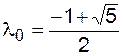 при k → ∞.
при k → ∞.
Поскольку числа Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, …
то получим значения 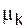 :
:
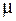 2 = 1,
2 = 1, 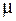 3 = 1/2,
3 = 1/2, 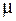 4 = 2/3,
4 = 2/3, 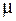 5 = 3/5,
5 = 3/5, 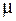 6 = 5/8,
6 = 5/8, 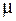 7 = 8/13, …
7 = 8/13, …
Свойство 2 леммы 3 можно уточнить:
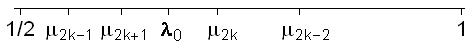 |
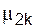
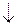
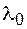 ,
, 
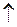
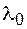 при k → ∞.
при k → ∞.
Лемма 4. Пусть λ выбирается из условий:
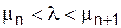 , если n – нечетное;
, если n – нечетное;
 , если n – четное.
, если n – четное.
Тогда для любых k = 1,2,…,n справедливы неравенства
0 <  k (λ) <
k (λ) <  k–1 (λ). (10)
k–1 (λ). (10)
Таким образом, при всяком λ, выбранном из условий леммы 4, согласно неравенствам (10) вложения
[ak, bk]  [ak–1, bk–1]
[ak–1, bk–1]
могут быть гарантированы только при k ≤ n.
Теорема 1. Если  , то справедливы свойства:
, то справедливы свойства:
1)  n (
n (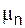 ) = 0;
) = 0;
2) для любых λ, удовлетворяющих условиям леммы 4, выполняются неравенства
0 <  n–2 (
n–2 (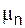 ) <
) <  n–2 (λ).
n–2 (λ).
Свойство 1) получается из формулы (9) при  = Fn–1/Fn:
= Fn–1/Fn:
 n =
n =  n (
n (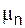 ) = (–1)n–1(Fn
) = (–1)n–1(Fn 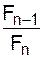 – Fn–1)
– Fn–1)  0 = 0.
0 = 0.
Свойство 2) 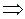 из леммы 4 с учетом равенства
из леммы 4 с учетом равенства
 n–2 (
n–2 (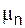 ) = (1/Fn)∙
) = (1/Fn)∙  0. (11)
0. (11)
Если n – нечетное, то при 
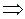
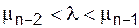
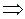
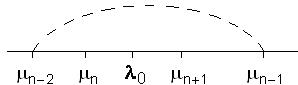
0 <  n–2 (λ) <
n–2 (λ) <  n–3 (λ). (12)
n–3 (λ). (12)
Если n – четное, то при 
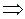
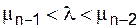
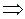 (12)
(12)
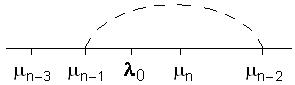
Тогда из свойства 1) на основании формулы (8) для длин вложенных отрезков поиска  k+2 =
k+2 =  k –
k –  k+1 при k = n – 2
k+1 при k = n – 2 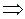
 |
 n =
n =  n–2 –
n–2 –  n–1 = 0
n–1 = 0 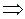
 n–2 =
n–2 =  n–1
n–1 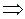 yn–3 = zn–3.
yn–3 = zn–3.
Итак, при заданном числе n нужно остановиться на (n–2)-м шаге.
Поэтому в методе Фибоначчи последовательность {  k (λ)} определяют такой, чтобы при заданном числе n выполнялось
k (λ)} определяют такой, чтобы при заданном числе n выполнялось
 n (λ) = 0,
n (λ) = 0,
тогда после n–2 шагов последовательность [ak, bk] стягивалась к точке 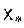 = yn–3 = zn–3.
= yn–3 = zn–3.
Схема метода.
Соответствует схеме метода золотого сечения при шагах k = 0,1,2,…,n–3.
Число n задано такое, чтобы выполнялось  n (λ) = 0.
n (λ) = 0.
Формулы вычисления промежуточных точек yk и zk на отрезке поиска [ak, bk]:
yk = ak + 
 0,
0,
zk = ak + 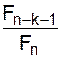
 0, k = 0,1,2,…,n–3.
0, k = 0,1,2,…,n–3.
Определим новый отрезок поиска [ak+1, bk+1]. Для этого сравним значения f(yk) и f(zk):
· если f(yk) ≤ f(zk) 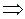 ak+1 = ak, bk+1 = zk, zk+1 = yk;
ak+1 = ak, bk+1 = zk, zk+1 = yk;
· если f(yk) > f(zk) 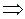 ak+1 = yk, bk+1 = bk, yk+1 = zk.
ak+1 = yk, bk+1 = bk, yk+1 = zk.
Выбор решения.
В качестве приближения для xmin выбирается точка
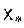 = yn–3 = zn–3,
= yn–3 = zn–3,
оставшаяся после n–2 шагов, для которой уже вычислено значение целевой функции.
Анализ метода.
1) Длины  k, k = 0,1,2,…n, можно вычислить заранее по формулам (8) или (9) при
k, k = 0,1,2,…n, можно вычислить заранее по формулам (8) или (9) при  = Fn–1/Fn.
= Fn–1/Fn.
2) Коэффициенты сжатия на каждом шаге 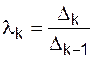 определяются равенством:
определяются равенством:
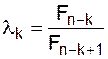 , k = 1,2,…n–1.
, k = 1,2,…n–1.
3) Из свойства 2 теоремы 1 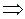 0 <
0 <  n–2 (
n–2 (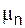 ) <
) <  n–2 (λ).
n–2 (λ).
Таким образом, при поиске точки минимума методом Фибоначчи через заданное число шагов получим отрезок наименьшей длины по сравнению с любым другим алгоритмом с последовательностью {  k (λ)} вида (8):
k (λ)} вида (8):  0 > 0,
0 > 0,  1 = λ∙
1 = λ∙  0,
0,  k+2 =
k+2 =  k –
k –  k+1.
k+1.
4) Вычислим коэффициент сжатия после n–2 шагов:
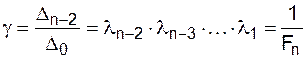 . (13)
. (13)
Длина  n–2 (
n–2 (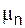 ) = (1/Fn)∙
) = (1/Fn)∙  0 (см. формулу (11))
0 (см. формулу (11))
5) В этом случае: погрешность определения точки xmin:
| 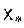 – xmin| ≤
– xmin| ≤  n–2 ≤ ε
n–2 ≤ ε
Тогда из формулы (13) 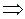 для достижения заданной точности результата ε > 0 число n выбирается из условия
для достижения заданной точности результата ε > 0 число n выбирается из условия
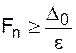 .
.
6) Степень близости полученного приближенного значения целевой функции и минимума этой функции на [a, b] определяется неравенством:
|f(xmin) – f(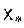 )| ≤ L∙|xmin –
)| ≤ L∙|xmin – 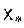 | ≤ L∙
| ≤ L∙  n–2 ≤ Lε.
n–2 ≤ Lε.
7) Общее количество m вычислений значений функции, требующее для достижения заданной точности ε > 0, равно
m = n – 2.
Коэффициент сжатия γ (величина отношения длин конечного и начального отрезков поиска) при данном алгоритме поиска после m вычислений значений функции равен γ = 1/Fm+2.
Например, коэффициент сжатия γ после m = 10 вычислений значений функции равен:
· для метода Фибоначчи γ = 1/F12 = 1/144 ≈ 0,00694;
(12 итераций)
· для метода золотого сечения γ = λm–1 ≈ (0,618)9 ≈ 0,013156.
(9 итераций)
т. е. почти в 1,895 раза длина конечного отрезка поиска для метода Фибоначчи меньше, чем для метода золотого сечения.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 635; Нарушение авторских прав?; Мы поможем в написании вашей работы!