Минимизация логических функций методом Куайна

[править]

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Метод Квайна — способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных.^[1][2][3]
Преобразование функции можно разделить на два этапа:

• на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме;
• на втором этапе — переход от сокращённой формы к минимальной форме.

Содержание

• 1 Первый этап (получение сокращённой формы)
• 2 Второй этап(табличный) (получение минимальной формы)
• 2.1 Импликантная матрица
• 3 Использование метода для получения минимальной КНФ
• 4 См. также
• 5 Примечания

[править] Первый этап (получение сокращённой формы)

Представим, что заданная функция представлена в СДНФ. Для осуществления первого этапа преобразование проходит два действия:

1. Операция склеивания;
2. Операция поглощения.

Операция склеивания сводится к нахождению пар членов, соответствующих виду или , и преобразованию их в следующие выражения: 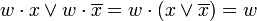. Результаты склеивания w теперь играют роль дополнительных членов.

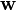Потом выполняется операция поглощения. Она основана на равенстве (член поглощает выражение ). Вследствие этого действия из логического выражения вычёркиваются все члены, поглощаемые другими переменными, результаты которых получены в операции склеивания.
Обе операции первого этапа могут выполняться до тех пор, пока это может быть осуществимо.
Применение этих операций продемонстрировано в таблице:

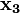
СДНФ выглядит так:

Результат операции склеивания нужен для преобразования функции на втором этапе (поглощения)

Членами результата склеивания являются

Член 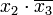поглощает те члены исходного выражения, которые содержат 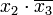, то есть первый и четвёртый. Эти члены вычёркиваются. Член поглощает второй и третий, а член — пятый член исходного выражения.

Повторение обеих операций приводит к следующему выражению:

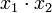Здесь склеивается пара членов и (склеивание пары членов и приводит к тому же результату), результат склеивания поглощает 2-, 3-, 4-, 5-й члены выражения. Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращённая форма выражения заданной функции (в данном случае она совпадает с минимальной формой)

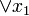
Структурная схема функции

Члены сокращённой формы (в нашем случае это 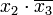и ) называются простыми импликантами функции. В итоге, мы получили наиболее простое выражение, если сравнивать его с начальной версией — СДНФ. Структурная схема такого элемента показана на рисунке справа.

[править] Второй этап(табличный) (получение минимальной формы)

Как и на первом этапе, в полученном равенстве могут содержаться члены, устранение которых никаким образом не повлияет на конечный результат. Следующий этап минимизации — удаление таких переменных. Таблица, представленная ниже содержит значения истинности функции, по ней будет собрана следующая СДНФ.

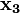
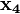
СДНФ, собранная по этой таблице выглядит следующим образом:

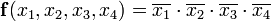
Конечное выражение достигается за счёт повторного использования операций склеивания и поглощения:

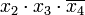
Члены этого выражения являются простыми импликантами выражения. Переход от сокращённой формы к минимальной осуществляется с помощью импликантной матрицы.
Члены СДНФ заданной функции вписываются в столбцы, а в строки — простые импликанты, то есть члены сокращённой формы. Отмечаются столбцы членов СДНФ, которые поглощаются отдельными простыми импликантами. В следующей таблице простая импликанта поглощает члены 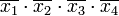и (в первом и во втором столбцах поставлены крестики).

[править] Импликантная матрица

Простая импликанта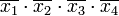

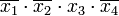
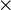
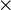
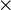
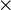
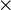
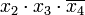
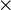
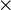
Вторая импликанта поглощает первый и третий члены СДНФ (указано крестиками) и т. д. Импликанты, не подлежащие исключению, образуют ядро. Такие импликанты определяются по вышеуказанной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только этой импликантой.
В нашем примере ядро составляют импликанты и (ими перекрываются второй и шестой столбцы). Исключение из сокращённой формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую в уже нелишний член.
Для получения минимальной формы достаточно выбрать из импликантов, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждом из этих импликант, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвёртый столбцы матрицы. Это может быть достигнуто различными способами, но так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать имликанту .
Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции:

Нажмите на изображение для его увеличения

(а)

Структурная схема, соответствующая этому выражению приведена на рисунке слева. Переход от сокращённой схемы к МДНФ был осуществлён путём исключения лишних членов — импликант и. Покажем допустимость подобного исключения членов из логического выражения.
Импликанты и становятся равными лог. 1 соответственно при следующих наборах значений аргументов: = 0, = 0, = 0 и = 1, = 1, = 0.
Роль этих импликант в выражении сокращённой формы функции заключается лишь в том, чтобы на приведённых наборах значений аргументов присваивать функции значение 1. Однако при этих наборах функция равна 1 из-за остальных импликант выражения. Действительно, подставляя набор значений, указанных выше в формулу (а), получаем:

• при = 0, = 0, = 0

;

• при = 1, = 1, = 0

;

[править] Использование метода для получения минимальной КНФ

Для получения Минимальной Конъюнктивной Нормальной Формы (МКНФ), используя метод Куайна, вводятся следующие критерии:

• для минимизации берётся не СДНФ, а СКНФ функции;
• склеиваемые пары членов меняются на: или;
• правило операции поглощения выглядит следующим образом:

[править] См. также

• Куайн, Уиллард Ван Орман
• Метод Куайна — Мак-Класки
• Карта Карно
• КНФ
• ДНФ

[править] Примечания

1. ↑ Краткое описание метода Квайна www.ptca.narod.ru
2. ↑ Лекция: Минимизация ФАЛ www.works.tarefer.ru
3. ↑ Пример минимизации переключательной функции методом Квайна matri-tri-ca.narod.ru

Источник — «http://ru.wikipedia.org/wiki/%D0%9C%D0%B8%D0%BD%D0%B8%D0%BC%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F_%D0%BB%D0%BE%D0%B3%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B9_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%BE%D0%BC_%D0%9A%D1%83%D0%B0%D0%B9%D0%BD%D0%B0»

Категории: Булева алгебра | Логика

Дата добавления: 2015-07-02