
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод половинного поділу відрізка
Мінімізація функцій однієї змінної.
Визначення 5. Функція 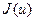 називається унімодальною на відрізку
називається унімодальною на відрізку  , якщо вона неперервна на
, якщо вона неперервна на 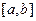 та існують числа
та існують числа 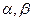 (a ≤
(a ≤ 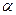 ≤
≤  ≤ b) такі, що:
≤ b) такі, що:
1) 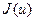 строго монотонно спадає при a ≤u ≤
строго монотонно спадає при a ≤u ≤ 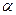 , якщо a<
, якщо a< 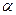 ;
;
2) 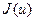 строго монотонно зростає при
строго монотонно зростає при  ≤u ≤ b, якщо
≤u ≤ b, якщо  < b;
< b;
3) 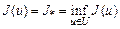 при
при 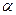 ≤ u ≤
≤ u ≤  , так що
, так що 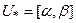 .
.
У випадку коли 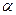 =
=  , функція
, функція 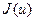 називається строго унімодальною на відрізку
називається строго унімодальною на відрізку 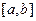 .
.
Слід відзначити, що якщо функція 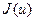 унімодальна на
унімодальна на 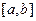 , то вона буде унімодальною і на будь-якому відрізку
, то вона буде унімодальною і на будь-якому відрізку 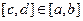 .
.
Цей метод є найпростішим методом мінімізації функції однієї змінної, який не потребує обчислення похідної. Будемо припускати, що мінімізуєма функція 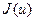 є унімодальною на відрізку
є унімодальною на відрізку 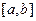 . Пошук мінімума починається з вибору двох точок
. Пошук мінімума починається з вибору двох точок 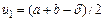 та
та 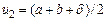 , де
, де  – константа, яка є параметром методу,
– константа, яка є параметром методу,  . Величина
. Величина  вибирається самостійно і може визначитися значимою кількістю вірних десяткових знаків при заданні аргументу u. Зокрема, зрозуміло, що
вибирається самостійно і може визначитися значимою кількістю вірних десяткових знаків при заданні аргументу u. Зокрема, зрозуміло, що  не може бути менше машинної похибки ЕОМ, яка використовується для розв’язання задачі. Точки
не може бути менше машинної похибки ЕОМ, яка використовується для розв’язання задачі. Точки 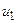 ,
, 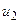 розміщені симетрично на відрізку
розміщені симетрично на відрізку 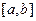 відносимо його середини та при малих б ділять його майже пополам (це і пояснює назву методу).
відносимо його середини та при малих б ділять його майже пополам (це і пояснює назву методу).
Після вибору точок 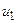 ,
, 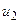 обчислюють значення
обчислюють значення 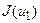 ,
, 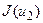 і порівнюються між собою. Якщо
і порівнюються між собою. Якщо  , то
, то 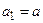 ,
, 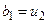 ; якщо ж
; якщо ж 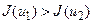 , то
, то 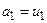 ,
, 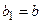 . Оскільки
. Оскільки 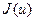 унімодальна на
унімодальна на 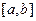 , то зрозуміло, що відрізок
, то зрозуміло, що відрізок 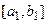 має спільну точку з множиною
має спільну точку з множиною 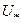 точок мінімуму
точок мінімуму 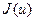 на
на 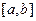 і його довжина дорівнює
і його довжина дорівнює
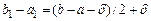 .
.
Нехай відрізок 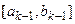 , який має непустий перетин з
, який має непустий перетин з 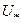 , вже відомий, і
, вже відомий, і
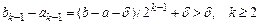 .
.
Тоді виберемо точки
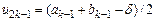 ,
,
 ,
,
які розміщені на відрізку 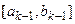 симетрично відносно його середини, і обчислюємо значення
симетрично відносно його середини, і обчислюємо значення 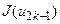 ,
, 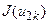 . Якщо
. Якщо 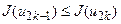 , то
, то 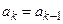 ,
,  ; якщо ж
; якщо ж 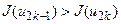 , то
, то 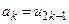 ,
, 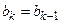 . Довжина відрізка
. Довжина відрізка 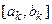 , який одержали, дорівнює
, який одержали, дорівнює
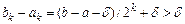 і
і 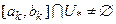 .
.
Якщо кількість обчислень значень функції не обмежена, то процес поділу відрізка можна продовжувати доки не отримаємо відрізок 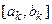 довжини
довжини 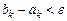 , де
, де 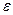 - задана точність,
- задана точність, 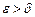 . Звідси маємо,
. Звідси маємо,
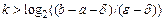 .
.
Оскільки, кожний поділ відрізка вимагає обчислення двох значень функції, то для досягнення точності 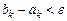 знадобиться всього
знадобиться всього  таких обчислень.
таких обчислень.
Після визначення відрізку 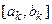 в якості наближення до множини
в якості наближення до множини 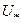 можна взяти точку
можна взяти точку
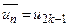 при
при 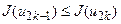
або
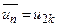 при
при 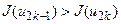 ,
,
а значення 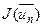 може виступати в якості наближення для
може виступати в якості наближення для 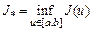 .
.
При такому виборі наближення для 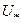 буде допущена похибка
буде допущена похибка 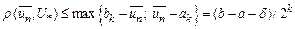 .
.
Якщо не вимагати того, щоб значення функції, яке є наближенним до 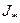 , було обчислене неодмінно в тій же точці, яка служить наближенням до
, було обчислене неодмінно в тій же точці, яка служить наближенням до 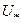 , то замість
, то замість 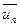 можна взяти точку
можна взяти точку 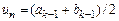 з меншою похибкою
з меншою похибкою
 ,
,
тут k = n/2 і  – достатньо мале.
– достатньо мале.
Зрозуміло, що в цьому випадку можна провести ще одне додаткове обчислення значення функції в точці 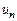 і покласти
і покласти 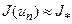 .
.
Зі сказаного вище слідує, що методом половинного поділу за допомогою n=2k обчислень значення функції можна визначити точку мінімуму унімодальної функції на відрізку 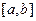 в кращому випадку з точністю
в кращому випадку з точністю 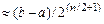 . Виникає питання про існування методів, які дозволяють за допомогою такої ж кількості обчислень значень функції розв’язати задачу мінімізації унімодальної функції точніше. Такі методи існують і один з них буде розглянуто в наступному пункті.
. Виникає питання про існування методів, які дозволяють за допомогою такої ж кількості обчислень значень функції розв’язати задачу мінімізації унімодальної функції точніше. Такі методи існують і один з них буде розглянуто в наступному пункті.
Відзначимо, що метод половинного поділу без змін можна застосовувати для мінімізації функції, які не є унімодальним. Але в цьому випадку не можливо гарантувати, що знайдений розв’язок буде достатньо точним наближенням до глобального мінімуму.
|
|
Дата добавления: 2015-07-02; Просмотров: 529; Нарушение авторских прав?; Мы поможем в написании вашей работы!