Недетерминированные и детерминированные А - грамматики

Представление А - грамматики в виде графа состояний.

Наглядным способом представления А-грамматики является граф состояний (переходов). Вершины этого графа соответствуют нетерминалам и из вершины A в вершину B проводится дуга, помеченная терминалом a, если в грамматике существует правило

A ® aB.

Добавим еще одну дополнительную заключительную вершину F и проведем дуги

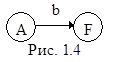
если в грамматике присутствует заключительное правило A ® b, а само это правило будем записывать A ® bF, получив тем самым модифицированную А-грамма­ти­ку.

Заметим, что каждому выводу в А-грамматике будет соответствовать путь по графу состояний из начальной вершины S в вершину F. Граф А-грамматики действительного числа из примера 1.9 представлен на рисунке 1.5 (a).

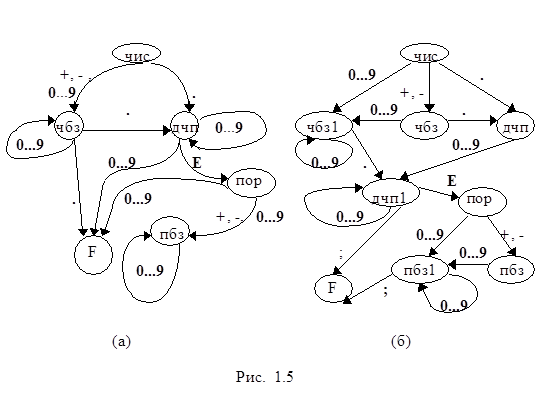
А-грамматика числа, рассмотренная в примере 1.9, является недетерминированной, то есть в ней существует такой нетерминал A и терминал a, для которых существует несколько нетерминалов B, таких что выполняются правила A ® aB. Например, модифицированная А-грамматика числа, что отчетливо видно на рис. 5.1 (а), содержит правила < чбз >®. < дчп > и < чбз >®. F или < дчп > ® 0< дчп > и < дчп > ® 0F. Это нежелательно с точки зрения построения программ синтаксического анализа.

А-грамматика называется детерминированной, если для любого A Î N (A ¹ F )и любого a Î S существует не более одного B Î N, для которого выполняется правило A ® aB.

А-грамматика называется вполне детерминированной, если для любого A ÎN (A ¹ F )и любого a Î S существует единственное B Î N, для которого выполняется правило A ® aB.

В разделе 3 будет показано, что любую недетерминированную А-грамматику можно свести к детерминированной. Пока же, для того чтобы перейти к реализации программ синтаксического анализа А-языков, что является основной частью лабораторных работ на ЭВМ в данной части курса, отметим, что на практике всегда используется специальный символ - ограничитель цепочки. Это либо нулевой байт, либо символ конца файла и т.п.

Если, например, считать, что число из примера 1.9 завершается символом “; ”, то детерминированная А-грамматика числа строится элементарно. Граф состояний для этого случая представлен на рис. 1.5 (б). Нетерминалы < чбз1 >, < дчп1 >, < пбз1 > добавлены здесь для того, чтобы исключить возможность формирования числа без целой и дробной части и без числа порядка после символа ” E ”. Вполне детерминированная форма должна включать, кроме того “ошибочный” нетерминал < Ош > и правила типа < чбз > ® + < Ош > или < дчп > ®. < Ош > и т.п. То есть для тех AÎ N (A ¹ F)и a Î S, для которых в модифицированной детерминированной А-грамматике нет правил A ® aB, необходимо для формирования вполне детерминированной формы добавить правила A ® aE, где E º <Ош> - “ошибочная” вершина.

Дата добавления: 2015-06-27