Влияние формы лопаток рабочего колеса насоса на значение теоретического напора

Напор

Основное уравнение центробежного насоса. Теоретический

Напор насоса связан со значением и направлением скоростей потока жидкости в межлопастных каналах рабочего колеса. Поэтому для вывода основного уравнения центробежного насоса – уравнения теоретического напора используют параллелограммы скоростей на входе и выходе жидкости из колеса (см. рис. 1.22), а также теорему об изменении моментов количества движения. Применительно к движению жидкости в каналах рабочего колеса насоса эта теорема формулируется так: прирощение момента количества движения 1 кг массы жидкости за время прохождения межлопастного пространства равно моменту импульсов всех внешних сил, приложенных к потоку от входа в канал до выхода из него за тот же промежуток времени t. Математически теорема записывается следующим образом:

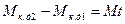, (1.38)

где		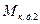- момент количества движения на выходе из рабочего колеса насоса;
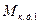
		- момент количества движения на входе в рабочее колесо насоса;
		- момент всех внешних сил относительно оси вращения колеса.

Следует отметить, что в межлопаточных каналах происходит cложное движение жидкости, относительные скорости в радиальных сечениях не одинаковы и параллелограммы скоростей входа и выхода потока отличаются. Учесть все явления происходящие в рабочем колесе, при выводе основного уравнения центробежного насоса не представляется возможным. Поэтому принимают следующие допущения:

1. Жидкость, перекачиваемая насосом считается идеальной, т.е. совер-шенно несжимаема, и в ней отсутствуют силы вязкости.

2. Считается, что условное рабочее колесо имеет бесконечно большое число бесконечно тонких лопаток. Тогда можно считать, что между лопатками будут элементарные потоки-струйки, и относительное движение в таких каналах можно характеризовать одним вектором скорости.

В уравнении (1.38) момент количества движении жидкости при входе в колесо относительно оси насоса (рис. 1.22) будет равен

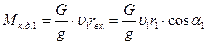, (1.39)

где - вес жидкости.

Момент количества движения на выходе из колеса

(1.40)

Для нахождения момента всех внешних сил , действующих на жидкость в межлопастных каналах относительно оси вращения колеса, необходимо установить эти силы. На жидкость в колесе действуют следующие силы:

1. Силы тяжести; момент этих сил относительно оси колеса всегда равен нулю, так как рассматриваемый объем представляет собой тело вращения и его центр тяжести находится на оси колеса.

2. Силы давления на поверхности контрольных сечений; эти силы про-ходят через ось вращения, и, следовательно, их момент так же равен нулю.

3. Силы трения жидкости на обтекаемых поверхностях; однако эти силы сравнительно невелики и в соответствии с принятыми допущениями их моментом можно пренебречь.

4. Силы воздействия на протекающую в межлопастных каналах жидкость сил давления со стороны лопастей рабочего колеса; момент этих сил не равен нулю.

Таким образом, момент всех внешних сил относительно оси колеса сводится к моменту динамического воздействия рабочего колеса 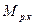на протекающую через него жидкость, т.е.

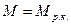(1.41)

В то же время известно, что мощность, передаваемая жидкости рабочим колесом насоса, равна

, (1.42)

где 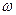- угловая скорость вращения колеса.

Следовательно 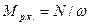, тогда

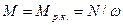(1.43)

С другой стороны, та же мощность 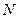определяется весом жидкости и напором .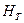

В результате получим выражение для произведения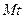

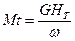(1.44)

где 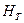- теоретический напор насоса.

Подставляя в (1.38) выражения (1.39), (1.40) и (1.44) и сокращая , получим

,

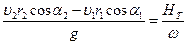или (1.45)

Так как 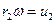, , 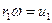окончательно получим

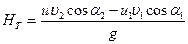(1.46)

Зависимость (1.46) называется уравнением Эйлера или основным уравнением лопастного насоса.

Основное уравнение показывает, что теоретический напор 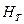, разви-ваемый насосом, тем больше, чем больше окружная скорость 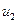на выходе жидкости из рабочего колеса, т.е. чем больше его диаметр 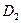и число обо-ротов 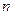(т.к. 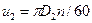). Повышение напора может быть также достигнуто уменьшением угла 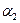Теоретически произведение 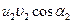имеет максимум при 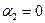, однако практически это означает прекращение подачи насосом. Поэтому при конструировании рабочих колес центробежных насосов обычно принимают .

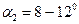При неизменных параметрах потока на выходе из рабочего колеса напор насоса, согласно основному уравнению, достигает максимума при условии

, (1.47)

что практически означает 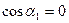или .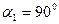

Учитывая, что в рабочее колесо жидкость поступает практически радиально (т.е. 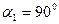), уравнение (1.46) принимает вид.

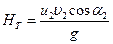(1.48)

Действительный напор, развиваемый насосом, меньше теоретического, так как необходимо учитывать конечное число лопастей в рабочем колесе и расходование напора на преодоление гидравлических сопротивлений.

С учетом этих поправок полный напор центробежного насоса составляет

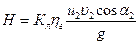, (1.49)

где		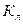- поправочный коэффициент, характеризующий уменьшение напора (за счет уменьшения скорости 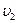) при наличии конечного числа лопастей рабочего колеса; ;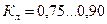
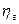
		- гидравлический КПД насоса; .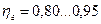

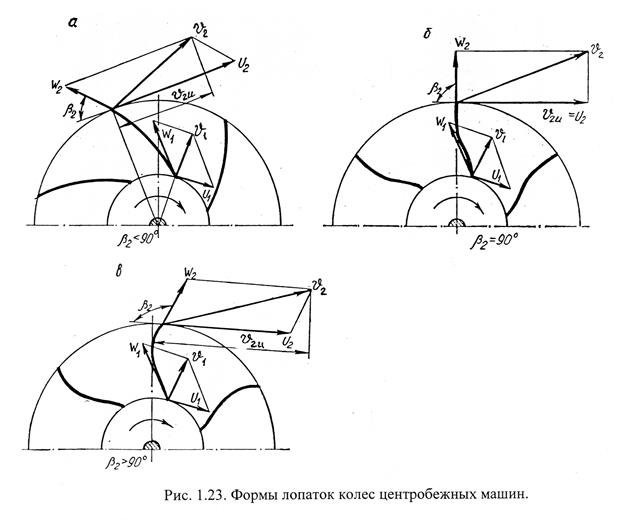
Существуют три вида лопаток: загнутые (по ходу вращения) назад (1.23, а); с радиальным выходом (рис. 1.23, б); загнутые вперед (1.23, в). Более совершенным является насос у которого напор развивается большей частью за счет статической энергии и в меньшей степени за счет динами-ческой энергии.

На основании уравнения (1.48) можно сделать вывод, что с увеличе-нием угла 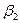напор насоса увеличивается за счет увеличения окружной составляющей 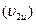абсолютной скорости. Следовательно, у рабочего колеса с лопатками, загнутыми вперед, он будет наибольшим. Однако в практике насосостроения чаще всего используют рабочие колеса с лопатками, загнутыми назад. Это объясняется тем, что у рабочих колес, с лопатками, загнутыми назад коэффициент стандартного напора 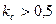, т.е. напор насоса создается большей частью за счет статической энергии. Следовательно, гидравлические потери при движении жидкости по каналам рабочего колеса будут меньше, а КПД насоса выше. У рабочих колес с радиальными лопатками 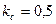, а с лопатками, загнутыми вперед .

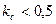Кроме того, лопатки загнутые назад, более удобообтекаемые при переменном режиме работы насоса, а диапазон скоростей безотрывного обтекания значительно шире. Обычно принимают следующие значения углов входа и выхода для лопаток, загнутых назад: 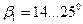и .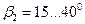

Дата добавления: 2015-07-02