Метод колебаний

При дополнительном грузе А на ободе колесо превращает­ся в физический маятник, который может совершать колеба­ния около положения устойчивого равновесия, соответствую­щего самому низкому положению груза А.

Если колесо повернуть от этого положения на некоторый угол, то вес груза А создаст относительно оси колеса вра­щающий момент: ; где l — расстояние центра тяжести груза A от оси вращения.

Уравнение движения колеса можно записать в виде:

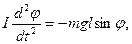
где I — момент инерции вращающейся системы, а ее угловое ускорение.

Для малых углов можно приближенно принять sinφ=φ и написать уравнение (8) в виде:

Это дифференциальное уравнение гармонических колебаний. Его решение:

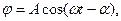
где , а А и α произвольные постоянные, определяющиеся начальными условиями.

Если при t = 0 груз неподвижен и угол φ имеет максимальное значение φ₀, то решение (10) принимает вид:

Угол φ — меняется по гармоническому закону с периодом

Соотношение (12) указывает простой путь для измерения момента инерции физического маятника. Очевидно:

и для вычисления момента инерции достаточно измерить мас­су дополнительного груза m, расстояние центра тяжести этого груза от оси вращения l и период колебаний маятника Т.

Масса m легко определяется взвешиванием, а l измеряется с помощью линейки и штангенциркуля.

Основной частью опыта в этом случае является определе­ние периода колебаний Т. Для этого даем колесу отклонения φ°, не более 15 градусов (от положения равновесия), секундо­мером определяем время t возможно большего числа колеба­ний п ивычисляем

Измерение Т нужно повторить не менее пяти раз и взять среднее из полученных значении. Найденное таким образом значение T _ср подставляем в (13) и вычисляем момент инер­ции I колеблющейся системы. Чтобы получить момент инер­ции I^k колеса, следует из I вычесть момент инерции оси и шки­ва (как в первом методе), а также момент инерции I "' относи­тельно оси вращения колеса дополнительного груза I^к = I – I' – I " – I "'

Дополнительный груз имеет форму цилиндра. Воспользо­вавшись теоремой Штейнера, можно вычислить I "':

Описанным способом определить I^k дважды (с двумя имеющимися при установке дополнительными грузами) и взять из полученных результатов среднее значение.

Вычислить абсолютную и относительную ошибки при из­мерении момента инерции колеса методом вращения и мето­дом колебаний. Указать основные источники ошибок в первом и втором методах.

Дата добавления: 2015-07-02