Общепринятая форма записи

Количество движения

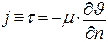- закон Ньютона – Петрова

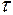
- касательное напряжение

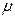- коэффициент динамической вязкости - количество движения, передаваемое в единицу времени через единицу поверхности при градиенте скорости, равному 1.

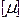
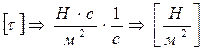- единица измерения давления.

2.13. Силы действующие в жидкости.

Вследствие текучести жидкости (подвижности ее частиц) в ней не могут действовать сосредоточенные силы, а возможно лишь действие сил, непрерывно распределенных по ее объему (массе) или по поверхности. В связи с этим силы, действующие на рассматриваемые объемы жидкости и являющиеся по отношению к ним внешними, разделяют на массовые (объем­ные) и поверхностные.

Массовые силы пропорциональны массе жидкого тела (сила тяжести, силы инерции и т.д.)

Поверхностные силы непрерывно распределены по поверхности жидко­сти и при равномерном их распределении пропорциональны величине этой поверхности. Эти силы обусловлены непосредственным воздействием сосед­них объемов жидкости на данный объем или же воздействием других тел соприкасающихся с данным жидким телом. В общем случае поверхностная 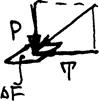сила действующая на площадку _DF под некоторым углом раскладывается на нормальную Р и тангенциальную T (касательную). Первая, если она направлена внутрь объ­ема, называется силой давления, вторая - силой трения. Массовые и поверхностные силы рассматриваются обычно в виде единич­ных сил, т.е. отнесенных к соответствующим единицам. Массовые силы от­носят к единице массы, поверхностные к единице поверхности.

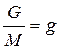Единичная массовая сила численно равна соответствующему ускорению, единичная поверхностная сила называется напряжением поверхностной силы. Нормальное напряжение:

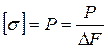
называется гидромеханическим (в случае покоя-гидростатическим) давле­нием или просто давлением. Если давление отсчитывается от нуля оно на­зывается абсолютным, если отсчитывается от атмосферного, то его называют избыточным (или манометрическим).

2.14. Характеристики движения жидкости.

Жидкой частицей называется малый объем жидкости или газа, кото­рый при движении деформируется и масса которого не смешиваются с ок­ружающей средой.

Движение жидкости характеризуется рядом геометрических и кинематических характеристик.

Скоростью жидкой частицы называется скорость какой-либо точки этой частицы, выбираемой произвольно. Оценивает путь, пройденный час­тицей в единицу времени,

ускорение оценивает, с какой быстротой меняется скорость частицы.

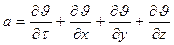
Частная производная 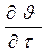выражает местное или локальное ускорение. Совокупность остальных членов в формулах называют конвективным ускорением.

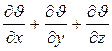
Линией тока называется кривая, в каждой точке которой в данный момент времени вектор скорости направлен по касательной. Система диф. уравнений линий тока имеет вид:

При установившемся движении линии тока совпадают с траекториями жид­ких частиц.

Совокупность линий тока, проведенных через малый замкнутый кон­тур, образует элементарную трубку тока. Часть потока заключенная виу^ три трубки тока называется струйкой. Элементарной. Потоки конечных размеров рассматриваются как совокупность элементарных струек. Если в потоке провести сечение нормальное линиям тока в каждой его точке, то такое сечение называется живым сечением.

Объемным потоком трубки тока называется величина:

поток вектора скорости через поверхность F определяется формулой:

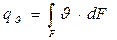
и называется объемным расходом через поверхность. Массовый расход будет равен: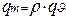

Единицы измерения расходов

2.15. Закон внутреннего трения (Закон Ньютона-Петрова)

В жидкости при наличии пере­мещения возникнут, и будут су­ществовать касательные напря­жения между соседними движу­щимися слоями. Ньютон предпо­ложил, что касательная сила (сила трения) может быть определена по следующей формуле:

где F - площадь соприкосновения сдоев, 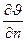градиент скорости, который показывает, как быстро меняется скорость в направлении перпендикуляр­ном перемещению. Сила Т действует в направлении противоположном перемещению. Напряжение от силы трения будет равно:

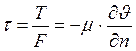
Соотношение (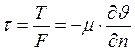) и является математическим выражением закона внутреннего трения. Напряжение внутреннего трения, возникающее меж­ду слоями жидкости при ее перемещении прямо пропорционально градиенту скорости. При движении жидкости происходит перенос количества движения в направлении перпендикулярном перемещению жидкости. Касательное напряжение можно рассматривать как удельный поток импульса, или количества движения, передаваемый через единицу поверхности в единицу времени:

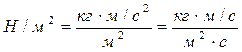
Таким образом, удельный поток импульса прямо пропорционален градиен­ту скорости.

2.16. Жидкости поведение которых подчиняется закону Ньютона называют - нормальными или Ньютоновскими. Однако в промышленности приходится иметь дело и с неньютоновскими жидкостями, т.е. жидкостями обладающими аномальными свойствами. Не подчиняются закону Ньютона растворы многих полимеров, коллоидные растворы, густые суспензии, резиновые смеси, пасты и др. Одной из разновидностей неньютоновских жидкостей являются бингамовские жидкости. Поведение их при сдвиговых нагрузках описывается уравнением:

Для описания поведения большой группы жидкостей используется уравне­ние Оствальда-де Билля:

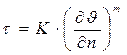
где K, m - константы, характеризующие течение жидкости. Если m<0, жидкости называются псевдопластическими, при m>0 дилатантными. Константы K, m определяется экспериментально, путем интерпретации кривых течения в логарифмических координатах: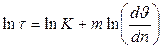

2.17. Уравнение неразрывности

Это уравнение устанавливает зависимость между скоростями в пото­ке жидкости, для которого соблюдается условие сплошности или неразрывности течения. Выделим в пространстве прямоугольный параллелепи­пед с гранями размером вдоль осей координат соответственно dx, dy, dz. Грани параллельны соответствующим осям. Составляющие скорости потока вдоль υx, υy, υz. Составим уравнение материаль­ного баланса для выделенного элементарного объема.

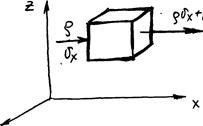
(Скорость накопления массы в элементарном объёме) = (Скорость подвода в элементарный объём) + (Скорость отвода из элементарного объёма)

Определим математически все составляющие уравнения (). Скорость накопления массы в элементарном объеме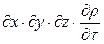

Скорость подвода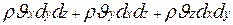

Скорость отвода:

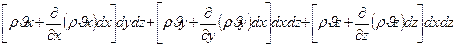После подстановки значений скоростей в уравнение () и преобразований, получим:

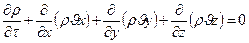
Если плотность по всем направлениям одинакова, т.е. жидкость не сжимаема, то уравнение примет вид:

Для стационарного режима будем иметь:

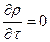и

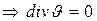
Для одномерного движения жидкости (наиболее часто встречающееся на практике) интегрирование уравнения () дает: (при постоянном живом сечении потока)

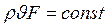
Если сечение потока переменно по его длине, то будем иметь:

2.18.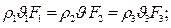

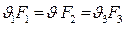
Это уравнение неразрывности в интегральной форме.

2.19. Дифференциальные уравнения движения вязкой жидкости Уравнения Навье-Стокса.

Рассмотрим движение вязкой (Ньютоновской) жидкости в поле дейст­вия сил тяжести. При движении в потоке жидкости действуют силы тяжес­ти, давления и трения. Выделим в пространстве прямоугольный паралле­лепипед с гранями dx, dy, dz и соорентируем эти грани параллель­но соответствующим координатным осям. Оси выберем таким образом, чтобы сила тяжести была направлена вдоль оси к плоскости уох. Рассмотрим равновесие выделенного элемента под

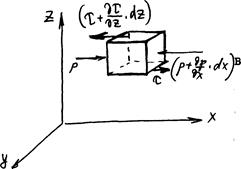
действием указанных сил. В соответствии с законом сохранения импульса из­менение количества движения в этом элементе будет равно сумме всех сил действующих на данный элемент:

(Изменение количества движения в элементарном объёме)

(Сумма сил, действующих на элемент)

Рассмотрим равновесие элемента в направлении оси X, а по осталь­ным осям запишем уравнения по аналогии. Равнодействующая от сил тре­ния будет равна

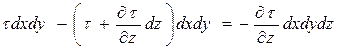
Но закону трения Ньютона-Петрова:

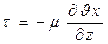
Тогда после подстановки

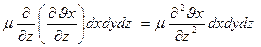
В общей случае составляющая скорости изменяется по всем направле­ниям и проекция составляющей силы трения на ось Х будет равна:

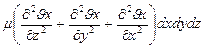
Равнодействующая сил давления будет равна:

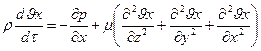
По принципу Д’Аламбера сумма всех сил действующих вдоль оси на выделенный элемент равна произведению его массы на ускорение:

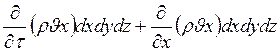
Подставляем значения всех слагаемых в уравнение () и получим математическое выражение, определяющее равновесие элемента вдоль оси X:

Аналогично рассуждая можно получить уравнения для осей У и Z, при этом необходимо помнить, что вдоль оси Z действует сила тя­жести:

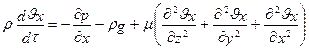
Полученная система уравнений носит название уравнений Навье-Стокса. Решение данной системы уравнений совместно с уравнением неразрыв­ности позволяет определить скорость движения точки в любой точке пространства и в любой момент времени. Аналитическое решение можно получить только для ряда конкретных примеров (течение в круглой трубе, течение по наклонной плоскости и т. д.) когда удается зна­чительно упростить исходные уравнения. Производная скорости в ле­вой части уравнений имеет сложный вид:

В зависимости от геометрии движущегося потока система уравнений может быть представлена в удобной системе координат.

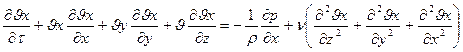
2.21. Уравнения гидростатики Эйлера.

В состоянии покоя скорость жидкости равна нулю и все члены уравнений Навье-Стокса содержащие производные скорости тоже равны нулю и система уравнений понимает вид:

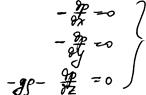
Полученная система уравнений носит название диффернциальных уравне­ний равновесия Эйлера. Данную систему уравнений можно интегрировать. Для этого каждое уравнение системы умножим соответственно на dx, dy, dz и сложим:

2.22.

После деления на dz получаем:

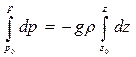
Интегрирование полученного уравнения дает:

Данное уравнение носит название основного уравнения гидростатики. Давление, создаваемое в любой точке покоящейся жидкости, передается всем точкам ее объема одинаково. При изменении P₂ на какую либо величину, давление P изменится на такую же величину.

Давление жидкости на плоскую наклонную стенку.

Необходимо определить силу давления по­коящейся жидкости на наклонную плоскую стенку, угол наклона которой к горизон­ту равен 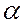. Так как величина давления переменна, определим силу давления на элементарную площадку dF в пределах

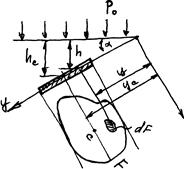
которой давление можно считать постоянным:

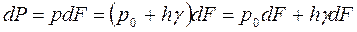
Проинтегрируем это уравнение:

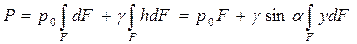
где 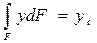, координата центра тя­жести площадки dF. Из механики извест­но, что интеграл в правой части представляет статический момент пло­щади F относительно оси X и равен произведению этой площади на ко­ординату ее центра тяжести y_c.Следовательно сила давления равна:

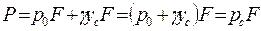
Таким образом, сила давления жидкости на плоскую стенку равна произве­дению площади стенки на величину гидростатического давления в центре тяжести этой площади.

2.23. Закон Архимеда

Определим силу, действующую на погруженное в жидкость тело.

Для простоты рассмотрим тело прямоуголь­ной формы. Найдем силу давления, действую­щую на тело. В силу симметрии силы дейст­вующие на боковые грани уравновешивают друг друга. Тело будет перемещаться под действием сил действующих на площадки 1-1 и 2-2:

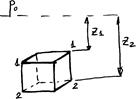
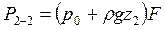
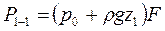
Равнодействующая сила:

Т.е. на тело погруженное в жидкость действует сила, выталкивающая, равная весу жидкости вытесненной телом.

Условия плавания тела: определяются путем сравнения веса тела и выталкивающей силы Архимеда:

P_a >G - тело плавает; P_a =G - нулевая плавучесть;

P_a <G - тело тонет.

Разница между весом тела и выталкивающей силой называется весом тела в жидкости.

Равновесие жидкости во вращающемся сосуде.

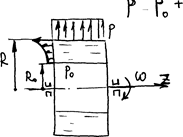
Сосуд с вертикальной осью вращения. Рассмотрим установившееся движение. Жидкость неподвижна относительно стенок сосуда. Движение можно рассматривать, как плоское в координатных осях r и z. Ось соориентированна вдоль оси цилиндра. Для плоского движения уравнения Эйлера будут иметь вид:

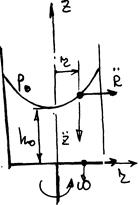
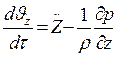
Массовые силы: вдоль оси r - центробежная сила инерции; вдоль оси z – сила тяжести в направлении, противоположном росту Z.

Умножим каждое уравнение соответственно на dr и dz, а затем сложим. После преобразования, получаем:

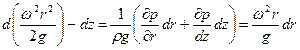
где 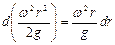- математическая сумма дифференциалов, равная дифференциалу суммы:

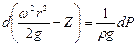
После интегрирования при граничных условиях r=0; z=h₀, получаем:

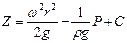
где С - постоянная интегрирования. Окончательно будем иметь:

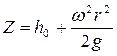
Таким образом, поверхность жидкости во вращающемся сосуде с вер­тикальной осью вращения имеет вид параболы.

Сосуд с горизонтальной осью вращения. Установившееся вращение цилиндра с постоянной угловой скоростью 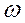.Движение можно рассматривать, как одномерное, вокруг оси Z, соорентированной перпендикулярно оси вращение цилиндра. Уравнение Эйлера:

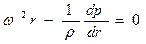
После разделения переменных и интегрирования при граничных условиях r=R₀; p=p₀ будем иметь:

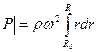
Таким образом, получаем возможность рассчитывать величину дав­ления жидкости на стенки и давление внутри жидкости при вра­щении цилиндра вокруг горизонтальной оси.

2.38. Уравнение Бернулли.

В гидравлике вводится понятие об идеальной жидкости, т.е. такой жидкости, у которой вязкость равна нулю. При движении такой жидкости касательные напряжения отсутствуют, и уравнение принимает вид:

Данная система уравнений называется уравнениями движения идеальной жидкости. Полученную систему уравнений можно проинтегрировать. Для этого умножим каждое из уравнений системы соответственно на dx, dy, dz и сложим левые и правые части уравнений:

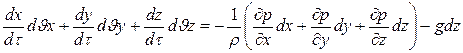
В левой части имеем:

, тогда

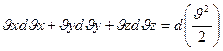, и вся скобка представляет собой дифференциал квадрата скорости. В правой части скобка представляет полный дифференциал давления. Таким образом, уравнение примет вид:

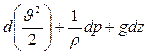
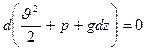, интегрирование последнего даёт:

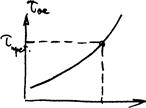
Полученное уравнение называется уравнением Бернулли для идеальной жидкости. Оно представляет собой частную форму закона сохранения энергии. Каждое слагаемое этого уравнения есть удельная энергия единицы веса (напор):

- кинетическая энергия; 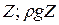- энергия положения; 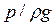- энергия давления.

Для трубопровода (двух его сечений) имеем:

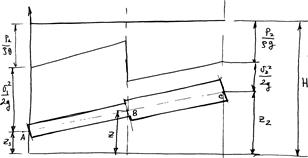
Графическая интерпретация уравнения Бернулли:

Гидромеханические процессы разделения гетерогенных жидкостей и газов.

Классификация процессов разделения. Процессы разделения гетероген­ных систем классифицируются следующим образом:

1) Осаждение. Гидромеханический процесс разделения гетерогенных сис­тем путем выделения из дисперсионной среды взвешенных в ней частиц дисперсной фазы под влиянием внешних массовых сил (сила тяжес­ти, сила инерции, электростатическая сила). К процессам осаждения относятся: отстаивание, циклонной процесс, отстойное центрифугирова­ние, электроочистка.

Отстаивание - процесс осаждения под действием сил тяжести. Аппараты, в которых осуществляется осаждение, называются отстойниками. Циклонный процесс - процесс разделения гетерогенных систем под дейс­твием вращательного движения жидкости или газа в неподвижном аппара­те. Аппараты для осуществления процесса называются циклонами или гидроциклонами.

Отстойное центрифугирование - отделение инородных частиц во вращающих­ся аппаратах, под действием центробежных сил. Машины, в которых осу­ществляется процесс, называются отстойными центрифугами. Электроочистка - процесс осаждения взвешенных частиц под действием электрического поля. Аппарат для осуществления процесса называется электрофильтром.

2) Пенный процесс - процесс очистки гетерогенных газов путем пропускания его через слой паны. Аппарат для проведения процесса - пенный.

3) Фильтрование - процесс разделения с помощью пористой перегородки, способной пропускать жидкость или газ, но задерживать взвешенные в дисперсионной среде твердые частицы. Оно осуществляется под дейст­вием сил давления или центробежных сил и применяется для более тонкого разделения суспензий и пылей, чем путем осаждения.

Основные параметры аппаратов для гидромеханического разделения.

Фильтрование - процесс разделения суспензий с использованием пористых перегородок, которые задерживают твердую фазу суспензии и пропускают ее жидкую фазу. Процесс осуществляется в аппаратах, разделенных на две части фильтровальной перегородкой. В фильтровальную перегородку входит решетка (опорная), металлическая сетка и фильтровальная ткань. В процессе фильтрования на перегородке задерживается взвешен­ная фаза, а поры в перегородке постепенно забиваются твердыми частицами.

Поэтому после­дующие операции процесса фильтрования - про­мывка осадка, продувка и сушка его. После промывки получают разбавленную смесь жидкой фазы суспензии ихини промывной жидкостью. Для удаления промывной жидкости проводят продувку осадка воздухом или инертным газом, а затем окончательно сушат осадок. Расчет фильтра периодического действия. Ведется следующим образом:

принимают наибольшую допустимую толщину осадка 6;

2)определяют время цикла фильтрования: .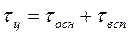

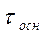- время фильтрования, определяется с помощью уравнения Рутса,

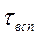- время вспомогательных операций (время подготовки, загрузка суспензии, удаления осадка);

3) выбирают тип аппарата и объем фильтра; определяют производительность фильтра

где 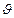- скорость осаждения в поле сил тяжести:

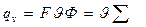
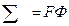- индекс производительности, он эквивалентен площади отстойника, имеющего такую же производительность, как данная центри­фуга. Выражение 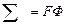справедливо для ламинарного режима осаждения.

Однако при больших скоростях вращения барабана центрифуги осаждение может происходить в переходном и турбулентном режимах:

переходный режим 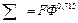; турбулентный режим .

Основные параметры аппаратов для гидромеханического разделения.

1. Производительность - количество очищенной дисперсионной среды, получаемой в единицу времени в аппарате.

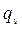- объёмная производительность м³/с

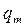- массовая производительность кг/ с

2. Коэффициент очистки - отношение количества взвешенных частиц, задержанных в аппарате, к общему количеству их в исходной гетерогенной смеси.

Рассмотрим схему такого аппарата. Составим уравнение материального баланса.

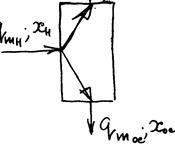
Пусть 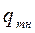, , 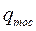- массовые расходы исходной смеси осадка, осветленной жидкости; X_н, X_к, X_ос массовые доли взвешенных частиц в исходной смеси, светленной жидкости и осадке. Уравне­ние материального баланса для установившего­ся режима работы имеет вид:

по общему количеству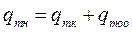

по дисперсной фазе

Решение позволяет определить производительность по светлой жидкости:

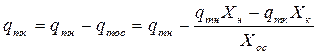
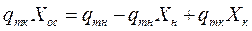
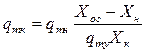
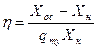- коэффициент очистки. Если все частицы задерживаются в аппарате, то to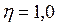

3. Мощность - энергия, которую необходимо затратить в единицу времени, чтобы осуществить процесс в данном аппарате или машине.

Гидравлическое сопротивление - разность давлений, которую необходимо приложить для движения гетерогенной жидкости или газа через аппарат:

где p₁ – давление на входе в аппарат, p₂ – давление на выходе из аппарата, 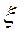- коэффициент местного сопротивления аппарата, - удельный вес жидкости или газа.

2.54. Процесс отстаивание.

Процесс применяется для разделения пыли, суспензии и эмульсий. Данный процесс является более дешевым, чем другие процессы разделения неоднородных систем, например, фильтрование. Отстаивание часто используют в качестве первичного процесса разделения, стараясь удалить большее количество дисперсное фазы из сплошной фазы.

Расчет отстойников. Основное требование которое должно выполняться при расчете аппарата состоит в том, что время пре­бывания смеси в аппарате равно или больше време­ни осаждения частицы (или всплывания), т.е.

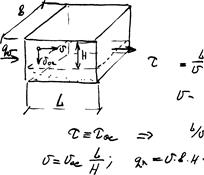
где - скорость жидкости, 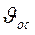- скорость осаждения.

Таким образом, производительность отстойника не зависит от высоты аппарата, а зависит от площади осаждения. Поэтому в отстойниках ста­раются увеличивать площадь осаждения при небольшой высоте, которая обычно не превышает 1,8-4,5. Эффективность определяется коэффициен­том очистки:

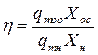
2.55. Типичные конструкции отстойников. Пылеосадительные камеры. Отста­ивание твердых частиц в газовой среде подчиняется тем же закономерностям, что и осаждение их под действием сил тяжести. Запыленный газ поступает в камеру 1, внутри кото­рой установлены горизонтальные перегородки 2 (полки). Частицы пыли осаждаются из газа при его движении между полками. Нали­чие полок позволяет увеличить поверхность осаждения частиц. Отражательная перегородка 3 позволяет дополнительно очистить газ при обтекании ее, за счет возникновения сил инерции. Кроме того, она выравнивает распределение газа по полкам т.к. выравнивает гидравлическое сопротивление всех полок.

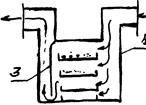
Пыль, осевшая на волках, удаляется с полок вручную или смывает­ся водой. Непрерывно-действующий конический отстойник. Для отстаивания небольших количеств жидкости применяют отстойники в виде вертикально установленных резервуаров с кони­ческим днищем, из которого непрерывно промывной водой удаляется осадок. Для отстаивания больших количеств жидкости, например для очистки сточных вод, используют или бассейны больших разме­ров или несколько последовательно соединенных резервуаров, работающих полунепрерывным спосо­бом. Отстойник полунепрерывного действия с наклонными перегородками.

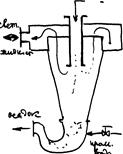
Исходная суспензия подается через штуцер 1 в корпус аппарата, внутри которого расположены наклонные перегородки 3. Наличие перегородок

увеличивает время пребывания и поверхности осаждения. Осадок собирается в конических днищах, откуда периодически удаляется, а осветленная жидкость через штуцер 4 отводится. В отстойниках непрерывного действия устанавлива­ется гребковая мешалка для непрерывного перемещения осаждающегося материала к разгрузочному отверстию.

2.58. Осаждение под действием центробежных сил в циклонных аппаратах.

2.59. Аппараты для очистки гетерогенных газов под действием центробеж­ных сил называются циклонами, а для очистки гетерогенных жидкос­тей гидроциклонами. Циклоны могут быть одиночными и батарейными. Циклон НИИОГаз. Запыленный газ входит по касательной к окружности, закручивается и движется по окружности, опускаясь вниз. Сделав 2-3 круга, газ уходит в выхлопную трубу. Частички прижимаются к стенке аппарата и под действием силы тяжести оседают. Технологи­ческие параметры: , , , , , .

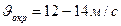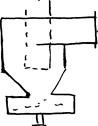
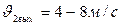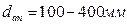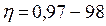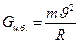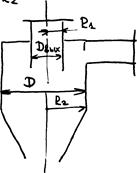
Для очистки больших объемов газа, циклоны устанавливаются в батарею. Причем вся батарея имеет одну и ту же подводящую и отводящую трубы. Так как , то, меньше R, тем больше , по­этому циклоны делают с малыми радиусами d_ап =150-250 мм и затем устанавливают в батарею. Такие циклоны называют батарейными. Число элементов 25-160, =730 м³/час, d = 250мм Расчет циклонного аппарата сводится к опре­делению его наружного диаметра. D_вых = 2R, Д = 2R₂.

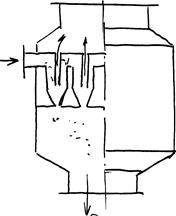
Под действием центробежных сил частицы твердой фазы отбрасываются к стенкам ротора и образуют осадок, а осветленная жидкость (фугат) переливаются через край ротора в корпус и удаляется из машины. Осадок удаляется либо периодически (в центрифугах периодического действия), либо может удаляться непрерывно с помощью специальных устройств (в центрифугах непрерывного действия). Центробежная сила в центрифугах зависит от фактора разделения:

или ;

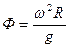
В зависимости от фактора разделения существует два типа центрифуг Ф<3500 нормальные, Ф>3500 сверхцентрифуги. Нормальные центрифуги используют для разделения суспензий, сверх­центрифуги для разделения суспензий с небольшим содержанием взвешен­ных частиц и для разделения эмульсий.

Производительность центрифуги. Производительность центрифуги равна объему Фугата, полученного в единицу времени. Для определения производительности используем основной принцип расчета отстойников:

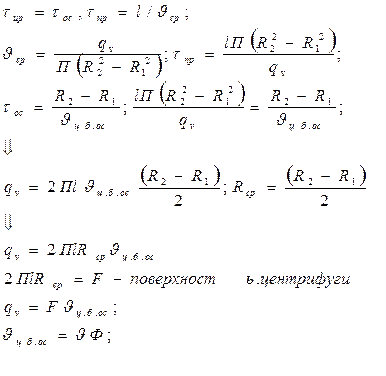
Закон Стокса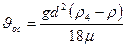

Принцип: время пребывания (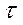) равно времени осаждения (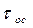). Расчет ведется для частицы минимального диаметра, которая может проскочить:

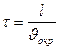
Так как частица делает n = 1,5-2,5 оборота, то .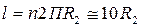

Для того чтобы определить , используем соотношение, полученное для расчета времени осаждения в поле центробежных сил:

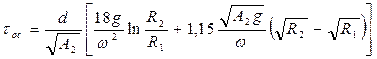
Определим R₁ из условия: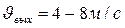

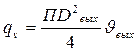
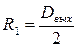
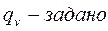
Подставляя R₁ в выражение для 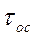получим трансцендентное уравнение, которое аналитически не решается. Его можно ре­шить графически: после определения R₂ которо­му выбирают циклон. Гидравлическое сопротивление циклонов:

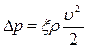
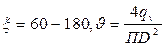
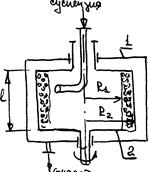
Отстойное центрифугирование. Центрифугирование - это процесс разделения неоднородных систем, таких как эмульсия и суспензия, в поле центробежных сил. Процесс центрифугирования проводят в машинах, называемых центрифугами.

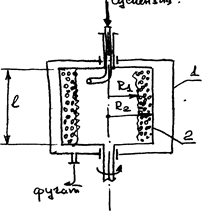
Общая характеристика процесса. В отстойных центрифугах проводят раз­деление суспензий на дисперсионную среду (фугат) и дисперсную (осадок). Центрифуга представляет собой машину, состоящую из цилин­дрического цилиндра (ротора). Ротор укрепляется на валу, который приводится во вращение электродвигателем, ротор помещается в непод­вижный корпус: 1-корпус, 2-ротор, 3-труба для подачи суспензии.

2.62. Электрическая очистка газов. Для высокой степени очистки газов применяют электрофильтры, у которых .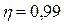

Физические основы процесса. Если между электродами поместить ионизированный газ, то создается направленное движение заряженных частиц, которые при своем движении могут также ионизировать воздух. Если между электродами пропускать запыленный газ, то ионы и элект­роны начнут двигаться к электродам и на своем пути, сталкиваясь с пылинками, будут сообщать им свой заряд и тем самым увлекать их к электродам. Обычно один из электродов - проволока, а второй труба, или пластина специального профиля. Электрофильтры чаще всего работа­ют при постоянном токе. Принципиальная схема установки для электри­ческой очистки газов, дана на рис. Расчет процесса электроочистки. Расчет сводится к определению скорости осаждения. Прежде всего, определяют фактор разделения

и силу электростатическо­го притяжения 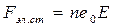где n - число зарядов, полученных частицей, е₀ – заряд электрона, Е - напряженность электрического поля.

Подставим вместо . Теперь необходимо определить скорость осаждения 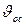по следующей ме­тодике: 1) находим Ф_эл; 2) определяем число Архимеда для электроста­тического поля ; 3) по формуле Тодеса находим число Рейнольдса 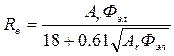; 4) находим скорость осаждения .

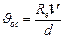Дата добавления: 2015-07-02