Прочитайте внимательно текст

ПЗ3А

Метод импликантных таблиц

Метод импликантных таблиц является одним из методов нахождения тупиковых и минимальных ДНФ по сокращенным ДНФ. Импликантная таблица представляет собой прямоугольную таблицу, столбцы которой соответствуют конституентам единицы исходной булевой функции, а строки — простым импликантам. В случае если простую импликанту можно получить из конституенты единицы вычеркиванием некоторых букв, то говорят, что импликанта накрывает (покрывает) конституенту. В этом случае клетка импликантной таблицы, соответствующая импликанте и конституенте, отмечается специальным знаком (например, звездочкой).

Пример 5. Заполним в соответствии с указанным выше правилом импликантную таблицу (табл. 2) для сокращенной ДНФ булевой функции, полученной в рассмотренном выше примере.

Таблица 2

Номер строки

Простые импликанты

Конституенты единицы

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

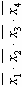
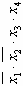
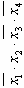
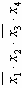
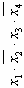
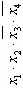
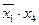
Минимальной ДНФ заданной функции будет соответствовать такая система минимального числа строк таблицы, импликанты которых совместно накрывают крестиками все колонки таблицы.

Для получения тупиковых ДНФ можно пользоваться следующими рекомендациями:

1. Выделяются все существенные (или обязательные) импликанты. Существенной импликанте соответствуют столбцы таблицы, в которых имеется только одна метка (звездочка). Она обязательно входит в минимальное покрытие, так как не используя ее, невозможно покрыть вое конституенты единицы.

2. Вычеркиваются столбцы таблицы, которым соответствуют выделенные существенные импликанты.

3. Выбирается такая совокупность оставшихся простых импликант после выделения существенных импликант, которая обеспечивает покрытие всех оставшихся столбцов таблицы с минимальной ценой.

Для рассматриваемого примера (табл. 2) возможны два варианта минимальных ДНФ:

Первый вариант соответствует системе строк, состоящей из 1, 4 и 5 строк; второй — из 2, 3 и 6 строк.

Дата добавления: 2015-07-02