Практическая работа № 14

ЗАДАНИЯ ПО ВАРИАНТАМ

Задача 1. Подобрать сечение сжатого стержня решетки стальной фермы при действии сжимающей нагрузки N. Предельная гибкость λ_макс= 210 - 60α. Толщина фасонки t_ф = 12 мм.

Исходные данные	Варианты
Геометрическая длина стержня l, м	3,1	2,8	3,0	2,8	2,9	3,0	3,1	2,5	2,4	2,6
Наименование стали	С235	С245	С255	С245	С275
Расчётное усилие N, кн
Геометрическая длина стержня l, м	3,6	3,3	3,6	3,3	3,9	3,5	3,2	3,0	2,8	3,2
Наименование стали	С245	С255	С275	С285	С345
Расчётное усилие N, кн
Геометрическая длина стержня l, м	4,1	3,8	4,2	3,8	4,5	4,0	3,3	3,5	3,4	3,6
Наименование стали	С255	С235	С245	С275	С285
Расчётное усилие N, кн

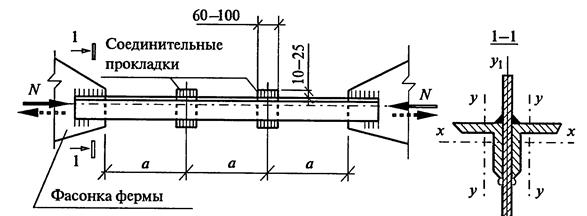
Ход решения.

1. Находим расчетное сопротивление стали R_y (таблица 1 Приложение 1)

2. Определяем коэффициент условия работы, предполагая, что гибкость стержня будет больше 60. (таблица 4 Приложение 3) γ_c = 0,8

3. Определяем расчетные длины стержня по табл.11 СНиП: (таблица 5 Приложение3) в плоскости фермы l_{ef x}= 0,8 l =… см

из плоскости фермы l_{ef y}= l =… см

4. Принимаем предварительно гибкость λ = 100 и находим коэффициент продольного изгиба φ (таблица 1 Приложение 3)

5. Находим требуемую площадь сечения стержня

см²

6. Определяем требуемые радиусы инерции: i_x =l_{ef x} /λ = см

i_y = l_{ef y} /λ = см

7. По сортаменту (таблица 3 Приложение 2) подбираем уголки по трем параметрам: А, i_x, i_y;

при подборе уголков не забываем, что площадь стержня состоит из двух уголков и требуемая площадь сечения одного уголка А_уг= А / 2. Принимаем уголок … ^х … с площадью А^табл_уг = …. см² больше `требуемой. Выписываем из сортамента i_x ^табл = … см; i_y^табл =… см.

8. Проверяем принятое сечение:

· определяем гибкости λ_х = l_{ef x} / i_x ^табл λ_у= l_{ef y} / i_y^табл

· по наибольшей гибкости определяем коэффициент продольного изгиба φ₂ = … (таблица 1 Приложение 3)

· находим значение коэффициента α = N / (φ_{2 *}2A^табл_{уг *} R_y* γ_c)

т.к значение коэффициента получилось больше 0,5 принимаем величину коэффициента α = … (если коэффициент получается меньше 0,5 то α = 0,5)

· определяем предельную гибкость λ_макс = 210 - 60α = …

Наибольшая гибкость стержня меньше предельной, следовательно, гибкость стержня в пределах нормы. (таблица 6 Приложение 3)

(Если нет, то необходимо принять другой размер уголка)

· Проверяем устойчивость σ = N / (φ_{2 *}2A^табл_уг ) = … ≤ R_y*γ_c,кН/см²

Вывод: Устойчивость обеспечена, принимаем сечение стержня из двух уголков размером … х ….

Задача 2. Подобрать сечение сжатого стержня решетки деревянной фермы при действии статической нагрузки N

Исходные данные	Варианты
Длина стержня l, м	3,1	2,8	3,0	2,8	2,9	3,0	3,1	2,5	2,4	2,6
Порода и сорт древесины	Лиственница 1 сорт	Сосна 1 сорт	Сосна 2 сорт	Кедр сибирский 1 сорт	Пихта 1 сорт	Лиственница 1 сорт	Лиственница 2 сорт	Кедр сибирский 1 сорт	Сосна 1 сорт	Сосна 2 сорт
Расчётное усилие N, кн

1. Находим расчетное сопротивление древесины R_c с учетом переходного коэффициента m_n (СНиП II-25-80) таблицы 2,3 Приложение 1

2. Определяем расчетную длину стержня в плоскости фермы l_ef,x

l_ef,x =0,8 l

3. Находим требуемую площадь сечения стержня, для этого предварительно принимаем гибкость стержня λ= 100 и по гибкости находим коэффициент продольного изгиба φ=0,434

А = N / φ R_c γ_c , см²

4. Находим минимальный радиус инерции по предельному значению гибкости.

- для верхнего пояса λ_пр=120;

- для элементов решетки λ_пр=150;

i = l_ef.x / λ_пр , см

5. Находим ширину сечения по значению радиуса инерции.

b_min = i / 0,29

6. Ориентировочно определяем высоту сечения h = A / b_min

7. По сортаменту (таблица 5 Приложение 2) назначаем размеры сечения стержня и определяем окончательную площадь сечения А₂

8. Проверяем сечение на устойчивость:

· Находим момент инерции I = b h³ /12

· Радиус инерции i₂ = √ I / A₂

· Гибкость λ₂ = l_ef.x / i₂

· Фактический коэффициент продольного изгиба φ₂ = …

если λ₂ < 70

если λ₂ ≥ 70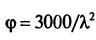

^· Проверяем устойчивость σ = N / A ₂ φ₂ ≤ R_с γ_с, кН/см²

Вывод: Устойчивость обеспечена, принимаем сечение стержня деревянной фермы размером … х ….

Контрольные вопросы

1. От чего зависит гибкость стержня фермы?

2. Какие виды деформаций испытывают стержни решетки фермы?

3. Как обеспечивается устойчивость сжатого стержня фермы?

Литература: В.И. Сетков «Строительные конструкции»,М.,

ИНФРА-М,2009, с. 332 – 335, 342 – 345

Тема: Определение расчетного сопротивления грунта и глубины заложения фундамента. Определение размеров подошвы фундамента.

Дата добавления: 2015-07-02