Обозначим

Решение начальных задач для дифференциальных уравнений.

Основные свойства преобразования Лапласа.

1. Свойство линейности:

,

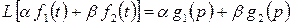где - любые комплексные числа; - изображения оригиналов .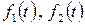

2. Свойство подобия:

.

3. Свойство запаздывания:

.

4. Свойство смещения:

.

5. Дифференцируемость оригинала:

(26)

В формулах (16) предполагается, что функции являются функциями конечного роста.

6. Дифференцируемость изображения:

7. Интегрирование оригинала:

.

8. Интегрирование изображения:

,

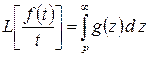при условии, что сходится.

Таблица преобразований Лапласа

№
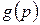
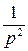
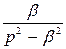
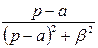
13

Примечание: - действительная часть комплексного числа; - мнимая часть.

Для изображения получаем

. Для изображения получаем

Домашнее задание:

Получите изображения функций

Решите начальные задачи:

где

.

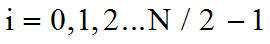Учтем, что,

Поэтому

Графическое представление вычислительных операций приведено на рисунке.

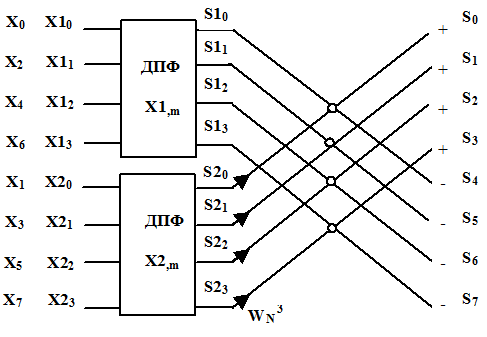
Стрелочками представлены множители

.

Отсчеты S₀, S₁, S₂, S₃ получаются с использованием операции сложения, поэтому около них стоит знак “ + “, отсчеты S₄, S₅, S₆, S₇ находятся после выполнения операции вычитания и около них поставлен знак “ - “.

Подсчитаем количество операций умножения, которые нужно выполнить, используя алгоритм БПФ.

Номер шага разбиения	Количество умножений на постоянный коэффициент	Количество блоков ДПФ, подлежащих дальнейшему разбиению	Вид последовательности на входах оставшихся блоков
	N / 2		N / 2
	2 (N / 4) = N / 2		N / 4
	4 (N / 8) = N / 2		N / 8
. . .	. . .	. . .	. . .
M -1	N / 2	2 ^M -1	N / 2 ^M -1 = 2
M	N / 2	-	-

На каждом шаге разбиения выполняется N / 2 умножений, количество шагов равно M = log ₂ N.

Следовательно, количество умножений равно (N / 2) log₂ N вместо N² при ДПФ.

Величина выигрыша при переходе от ДПФ к БПФ увеличивается с увеличением количества отсчетов N.

4.4. Алгоритм БПФ с прореживанием по частоте

Пусть имеется исходная N - точечная последовательность x_n, где N = 2^M. Разобьем члены этой последовательности на две группы. В первую включим первую половину членов исходной последовательности, а во вторую группу - вторую половину. Из первой группы образуем последовательность x1_m, а из второй - последовательность x2_m.

Индексы последовательностей x_n и x1_m связаны соотношением n = m, а индексы последовательностей x_n и x2_m - соотношением n = N/ 2 + m.

Тогда

Дата добавления: 2015-07-02