Программа зачета по алгебре

1. Степень с целым показателем. Определения и свойства.

2. Арифметический корень n-й степени. Определения и свойства.

3. Степень с рациональным показателем. Определения и свойства.

4. Принцип математической индукции. Примеры использования.

5. Доказательство неравенств. Неравенство Бернулли и неравенство Коши.

6. Равносильность уравнений и неравенств. Равносильные преобразования иррациональных уравнений и неравенств. Схемы решений уравнений и неравенств с модулем.

7. Многочлены. Степень многочлена, равенство многочленов. Сложение и умножение многочленов.

8. Деление многочлена на многочлен. Теорема о делении многочленов с остатком. Делимость многочленов, свойства делимости.

9. Теорема Безу, следствия. Число вещественных корней многочлена, кратные корни.

10. Схема Горнера, теорема Виета.

11. Рациональные корни алгебраического уравнения с целыми коэффициентами. Признак неразрешимости а.у. в рациональных числах.

12. Логарифмы. Определение и действия с логарифмами. теорема о свойствах.

13. Бинарные операции на множествах. Замкнутость. Свойства операций.

14. Группы и поля. Поле рациональных чисел (проверка аксиом).

15. Тригонометрия: основные определения, формулы сложения, половинного, двойного и тройного аргумента, формулы приведения, формулы универсальной подстановки, преобразование суммы триг. функций в произведение и обратно.

16. Арксинус и арккосинус числа: определение и свойства. Решение уравнени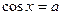й и 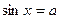, решение соотв. неравенств.

17. Арктангенс и арккотангенс числа: определение и свойства. Решение уравнени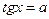й и 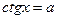. решение соотв. неравенств.

18. Определение множества комплексных чисел (к. ч.). Сложение и умножение к. ч., проверка аксиом поля.

19. Алгебраическая форма к.ч. Равенство к.ч. в алг.форме. Действия с к.ч. в алг. форме. Сопряженные и противоположные к.ч., свойства.

20. Модуль компл. числа. Свойства, геометрический смысл.

21. Тригонометрическая форма комплексных чисел. Действия с к.ч. в тригонометрической форме.

22. Основные ГМТ комплексной плоскости (окружность, прямая, круг и полуплоскость), их задание уравнениями и неравенствами. Преобразования на комплексной плоскости с использованием алгебраической и тригонометрической формы комплексного числа..

23. Степень к. ч., формула Муавра. Корни n-ной степени из комплексного числа.

24. Извлечение квадратного корня из к. ч. в алгебраической форме.

25. Теорема о комплексно-сопряженных корнях алгебраического уравнения с вещественными коэффициентами. Основная теорема алгебры (б/д). Следствия о числе корней и о разложении на линейные множители с комплексными коэффициентами, о разложении на квадратичные множители с вещественными коэффициентами..

26. Теорема Виета для многочленов над полями вещественных и комплексных чисел.

Дата добавления: 2015-07-02