Теоретические основы эксперимента. Действует гибкая система скидок и поощрений!!!

Действует гибкая система скидок и поощрений!!!

ТРАНСПОРТИРОВКИ ГАЗА

[e-mail]

ТРУБЫ ПОЛИЭТИЛЕНОВЫЕ ДЛЯ

	Трубы из полиэтилена высокой плотности (HDPE) класса ПЕ-80 диаметром от 20 до 400 мм, предназначенные для транспортировки газа под давлением до 0,6 МПа (6 атм.)

Материал: HDPE, PE 80
Внешний диаметр трубы (мм)	SDR 17,6 (0,3 Мпа)	SDR 11 (0,6 Мпа)	В бухте, (м.п.)
Толщина стенки (мм)	Масса (кг/м)	Цена за 1 м.п. грн.	Толщина стенки (мм)	Масса (кг/м)	Цена за 1 м.п. грн.
	-	-	-	3,0	0,123	-	100 - 300
	-	-	-	3,0	0,209	9.61	100 - 300
	-	-	-	3,0	0,276	12.70	100 - 300
	-	-	-	3,7	0,427	19.64	100 - 200
	2.9	0.443	20.39	4.6	0.663	30.50	100 - 200
	3.6	0.691	31.79	5.8	1.050	48.30	100 - 200
	4.3	0.97	44.65	6.8	1.462	67.25	100 - 200
	5.2	1.40	64.40	8.2	2.12	97.52
	6.3	2.070	95.22	10.0	3.14	144.44
	7.1	2.660	122.36	11.4	4.080	187.68
	8.0	3.330	153.18	12.7	5.080	233.68
	9.1	4.340	199.64	14.6	6.70	308.20
	10.3	5.519	253.92	16.4	8.429	387.78
	11.4	6.781	311.88	18.2	10.395	478.40
	12.8	8.55	393.30	20.5	13.157	607.20
	14.2	10.554	487.60	22.7	16.181	749.80
	15.9	13.200	611.80	25.4	20.300	938.40
	17.9	16.700	772.80	28.6	25.700	1154.60
	20.2	21.200	979.80	32.2	32.600	1508.80
	22.7	26.900	1242.00	36.3	41.400	1922.80

Процесс переноса тепла между твердой стенкой и омывающей ее жидкостью называется конвективным теплообменом или теплоотдачей. Тепло при этом будет переноситься совокупным воздействием теплопроводности и конвекции. В зависимости от причины, вызывающей течение жидкости, движение может быть свободным и вынужденным. Свободными называются течения, происходящие вследствие воздействия неоднородного поля массовых сил, приложенным к элементам массы внутри рассматриваемой системы и обусловленные внешними полями (гравитационными, магнитными, электрическими). Свободное движение под действием гравитационного поля при неравномерном распределении плотности жидкости называется свободным гравитационным движением или свободной гравитационной конвекцией. Перенос тепла жидкостью при ее свободном движении называется теплоотдачей при свободной конвекции. Неоднородность распределения плотности при этом может быть вызвана самыми различными причинами: неоднородность распределения температуры, различной по объему концентрации некоторого компонента в смеси, наличием фаз с различной плотностью.

Вынужденным считается движение жидкости, вызванное посредством подвода к жидкости механической энергии от посторонних устройств – насоса, компрессора, вентилятора. Вынужденное течение почти всегда сопровождается свободным. Причем влияние последнего тем больше, чем больше перепад плотности в отдельных элементах объема жидкости.

Интенсивность процесса обмена теплом определяется коэффициентом теплоотдачи. Осредненный по поверхности коэффициент теплоотдачи может быть рассчитан по формуле Ньютона

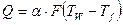, (1.1)

где 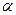- коэффициент теплоотдачи;

F – площадь поверхности;

T_W – температура поверхности;

T_f – температура омываемой среды.

С физической точки зрения коэффициент теплоотдачи представляет количество тепла, переданное в единицу времени через единицу поверхности при температурном напоре 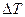в один градус.

Процесс теплоотдачи неразрывно связан с характером течения жидкостей. Характер движения теплоносителя около стенки зависит от формы поверхности ее положения в пространстве и направления теплового потока. На рисунке 1.1 показана картина движения теплоносителя около охлаждаемой вертикальной стенки (а),около охлаждаемых (б, в)и около нагреваемых горизонтальных поверхностей (г, д).

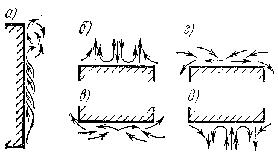
Рисунок 1.1 – Движение теплоносителя

Движение теплоносителя вдоль охлаждаемой вертикальной стенки в нижней части имеет ламинарный характер, выше — переходный, а затем - вихревой. В случае нагреваемой стенки тепло­носитель перемнется сверху вниз, и характер течения изменится в той же последовательности. Режим течения определяется главным образом температурным напором, с увеличением которого сокращается длина участка, занятого ламинарным потоком, и увеличивается зона вих­ревого движения. На участке ламинарного движения коэффициент теплоотдачи уменьшает­ся в соответствии с увеличением толщины ламинарного слоя тепло­носителя. В зоне вихревого движения коэффициент теплоотдачи имеет практически одинаковое значение для всей поверхности.

Характер движения теплоносителя около плоских горизонталь­ных поверхностей зависит от их расположения и направления теп­лового потока. При картине движения, отвечающей схемам в и г, поверхность стесняет движение теплоносителя, и потому теплообмен протекает менее интенсивно, чем в случаях б и д.

Характер свободного движения теплоносителя в ограниченном пространстве зависит от формы и взаимного расположения поверх­ностей, образующих прослойку, а также от расстояния между ними.

Движение теплоносителя по-разному протекает в замкнутых и открытых прослойках.

На рисунке 1.2 рассмотрены два случая теплоотдачи при свободном движении теплоносителя в ограниченном пространстве: теплоотдача в замкнутой прослойке (а) и теплоотдача в открытом зазоре при одинаковой температуре стенок, образующих зазор (б).

Рисунок 1.2 – Теплоотдача при свободном движении

теплоносителя в ограниченном пространстве

При теплоотдаче в замкнутом пространстве перенос теплоты осуществляется одним и тем же теплоносителем, который циркулирует между горячей и холодной стенками, образуя замкнутые контуры. В этом случае трудно отделить теплоотдачу около охлаждаемой и нагреваемой поверхностей. Поэтому процесс теплообмена в замкнутой прослойке оценивают в целом, определяя плотность теплового потока формулой теплопроводности

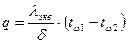, (1.2)

где 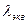— эквивалентный коэффициент теплопроводности;

d — толщина прослойки.

Эквивалентный коэффициент теплопроводности учитывает ин­тенсивность циркуляции в прослойке и определяется через коэффициент теплопроводности теплоносителя формулой

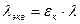, (1.3)

где 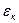— коэффициент конвекции.

Опытное исследование теплоотдачи в замкнутом пространстве показало, что независимо от формы прослойки коэффициент кон­векции можно определить из уравнения

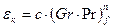(1.4)

в котором с и п зависят от величины произведения 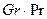. При 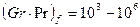значения с = 0,105 и n = 0,3, при 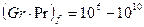с = 0,4 и п = 0,2. При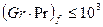 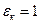, т. е. циркуляция отсутствует, и теплота передается только теплопровод­ностью.

В уравнении (1.4) за определяющую выбрана средняя температура теплоносителя, равная полусумме температур стенок, а за определяющий размер — толщина прослойки d.

Опытное изучение теплоотдачи в открытом зазоре при свободном движении воздуха между вертикальными стенками, имеющими одинаковую температуру, показало, что существует критическая величина зазора, при которой теплообмен достигает наибольшей интенсивности. При зазорах меньше критического интенсивность теплообмена резко ухудшается, а при зазорах больше критического — остается практически неизменной. При теплоотдаче в воздухе кри­тическая величина зазора определяется из равенства

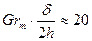, (1.5)

где d — расстояние между стенками;

h — высота стенки.

При подсчете числа Gr за определяющий размер принята половина расстояния между стенками.

Максимальная интенсивность теплообмена достигается при условиях, когда толщина пограничного слоя становится равной половине расстояния между стенками.

Теплоотдача в зазоре протекает более интенсивно, чем при свободном движении около одиночной пластины. При расстояниях между вертикальными стенками, близких к критическим (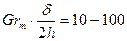), опытные данные по теплоотдаче удовлетворительно описываются уравнением

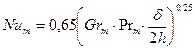(1.6)

Определяющий размер здесь выбирается так же, как в уравнении (1.5).

При некоторой скорости, определенной для каждого конкретного рассматриваемого случая движения жидкости, происходит изменение режима. Скорость, при которой наступает процесс изменения режима течения, носит название критической скорости. Переход из ламинарного в турбулентный режим течения осуществляется не мгновенно, а на некотором участке, режим течения на котором носит название переходного, участок II (рисунок 1.3) На участке III имеет место турбулентное течение.

.

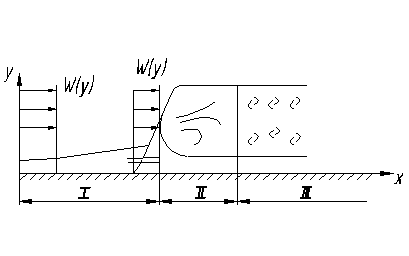
Рисунок 1.3 – Обтекание горизонтальной пластины жидкостью

Режимы течений определяются безразмерным комплексом – критерием Рейнольдса

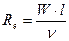, (1.7)

где W – скорость течения жидкости, ;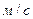

l – характерный размер, ;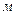

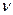- коэффициент кинематической вязкости, .

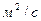Переход ламинарного течения в турбулентное происходит при критическом значении числа Рейнольдса 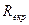. При движении в трубах величина

,

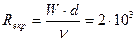где d – характерный размер, в рассматриваемом случае внутренний диаметр трубы.

Математическое описание процесса теплоотдачи включает в себя дифференциальное уравнение: теплопроводности, движения, сплошности и условия однозначности.

Аналитическое решение перечисленной системы уравнений для большинства задач процессов теплообмена в настоящее время не представляется возможным. Таким образом, большая роль в изучении процессов теплообмена отводится эксперименту и к обобщению на основе его с использованием основ теории подобия физических явлений.

Гравитационная, свободная конвекция возникает, как уже отмечалось, из-за различия плотностей нагретых и холодных частей сплошной среды. Зависимость плотности от температуры для большинства сред в диапазоне температур, наиболее часто встречающемся на практике, может аппроксимироваться линейным законом.

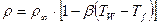, , (1.8)

где 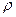- плотность жидкости;

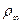- плотность жидкости на достаточном удалении от нагретой стенки;

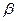- температурный коэффициент объемного расширения среды.

Как видно из выражения (1.8) 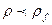если 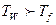; это приводит к возникновению подъемной архимедовой силы. Эта сила и является источником

свободного движения среды.

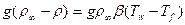(1.9)

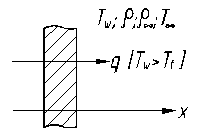
Рисунок 1.4

Условия подобия процессов естественной конвекции состоят из общепринятых, рекомендованных теорией подобия. Прежде всего, необходимым условием подобия является геометрическое подобие рассматриваемых процессов теплообмена, и подобие температурных полей. Подобие процессов свободной конвекции определяется критериями подобия – критерием Грасгофа 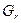и критерием Прандтля .

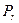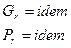
Физический смысл критерия 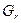может быть выражен как отношение подъемной силы к силе трения.

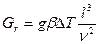(1.10)

Критерий Прандтля указывает на степень подобия полей температуры и скорости.

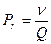, (1.11)

где Q – коэффициент температуропроводности.

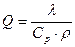(1.12)

При выполнении условий в сравниваемых процессах будет одинаковым и определяемый критерий – критерий Нуссельта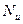

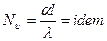, (1.13)

где α – коэффициент теплоотдачи;

λ – коэффициент теплопроводности среды.

Определяющие критерии составляются из условий однозначности. Определяемые критерии в подобных явлениях получаются идеальными как следствие равенства определяющих критериев. Связь между определяющими критериями представляет собой критериальные уравнения.

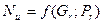
Для горизонтальных труб в диапазоне 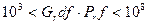критериальное уравнение имеет

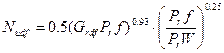(1.14)

А для вертикальных поверхностей зависимость следующая, при 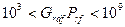(ламинарный режим)

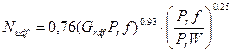(1.15)

При 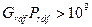(турбулентный режим)

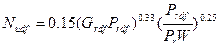(1.16)

Для газов 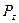=const=0,7, а 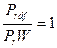, что упрощает расчетные формулы.

Расчетная формула для ламинарного течения около горизонтальной трубы преобразуется

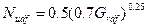(1.17)

Для вертикальных труб ламинарный режим

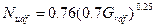(1.18)

Турбулентный режим

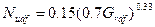(1.19)

Из определения критерия 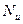находится осредненный коэффициент теплоотдачи

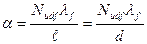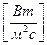, (1.20)

При свободном движении жидкости в неограниченном пространстве параметры течения значительно изменяются в пограничном слое.

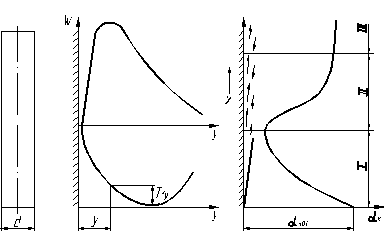
Рисунок 1.5 – Изменение параметров свободного течения вдоль вертикальной трубы

Скорость свободного течения изменяется от 0 у стенки до своего максимального значения на некотором удалении от стенки и вновь приближается к 0 на достаточно большом от стенки расстоянии. Температура жидкости непосредственно у стенки равна температуре стенки, и она будет падать с удалением от стенки.

На начальном участке толщина пограничного слоя мала и движение носит струйный ламинарный характер. При таком течении из-за роста толщины пограничного слоя теплоотдача падает и коэффициент теплоотдачи на участке (I) снижается.

На участке II, где имеет место переходный режим течения, коэффициент теплоотдачи возрастает, оставаясь меньше начального значения , и на участке III α остается почти постоянным. Некоторое снижение α на участке III объясняется ростом толщины ламинарного подслоя.

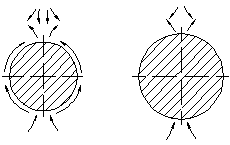
Рисунок 1.6 – Свободное течение жидкости около горизонтальных труб

Дата добавления: 2015-06-27