Задачи лексического анализа

Проиллюстрируем работу алгоритма на примере.

Пусть задан НКА M = ({H, A, B, S}, {0, 1}, F, {H}, {S}), где

F(H, 1) = B F(B, 0) = A

F(A, 1) = B F(A, 1) = S,

тогда соответствующий детерминированный конечный автомат будет таким:

K’ = {[H], [A], [B], [S], [HA], [HB], [HS], [AB], [AS], [BS], [HAB], [HAS], [ABS], [HBS], [HABS]}

F’([A], 1) = [BS] F’([H], 1) = [B]

F’([B], 0) = [A] F’([HA], 1) = [BS]

F’([HB], 1) = [B] F’([HB], 0) = [A]

F’([HS], 1) = [B] F’([AB], 1) = [BS]

F’([AB], 0) = [A] F’([AS], 1) = [BS]

F’([BS], 0) = [A] F’([HAB], 0) = [A]

F’([HAB], 1) = [BS] F’([HAS], 1) = [BS]

F’([ABS], 1) = [BS] F’([ABS], 0) = [A]

F’([HBS], 1) = [B] F’([HBS], 0) = [A]

F’([HABS], 1) = [BS] F’([HABS], 0) = [A]

S’ = {[S], [HS], [AS], [BS], [HAS], [ABS], [HBS], [HABS]}

Достижимыми состояниями в получившемся КА являются [H], [B], [A] и [BS], поэтому остальные состояния удаляются.

Таким образом, M’ = ({[H], [B], [A], [BS]}, {0, 1}, F’, H, {[BS]}), где

F’([A], 1) = [BS] F’([H], 1) = [B]

F’([B], 0) = [A] F’([BS], 0) = [A]

Лексический анализ (ЛА) - это первый этап процесса компиляции. На этом этапе символы, составляющие исходную программу, группируются в отдельные лексические элементы, называемые лексемами.

Лексический анализ важен для процесса компиляции по нескольким причинам:

a) замена в программе идентификаторов, констант, ограничителей и служебных слов лексемами делает представление программы более удобным для дальнейшей обработки;

b) лексический анализ уменьшает длину программы, устраняя из ее исходного представления несущественные пробелы и комментарии;

c) если будет изменена кодировка в исходном представлении программы, то это отразится только на лексическом анализаторе.

Выбор конструкций, которые будут выделяться как отдельные лексемы, зависит от языка и от точки зрения разработчиков компилятора. Обычно принято выделять следующие типы лексем: идентификаторы, служебные слова, константы и ограничители. Каждой лексеме сопоставляется пара (тип_лексемы, указатель_на_информацию_о_ней).

Соглашение: эту пару тоже будем называть лексемой, если это не будет вызывать недоразумений.

Таким образом, лексический анализатор - это транслятор, входом которого служит цепочка символов, представляющих исходную программу, а выходом - последовательность лексем.

Очевидно, что лексемы перечисленных выше типов можно описать с помощью регулярных грамматик.

Например, идентификатор (I):

I ® a|b|...|z|Ia|Ib|...|Iz|I0|I1|...|I9

целое без знака (N):

N® 0|1|...|9|N0|N1|...|N9

и т.д.

Для грамматик этого класса, как мы уже видели, существует простой и эффективный алгоритм анализа того, принадлежит ли заданная цепочка языку, порождаемому этой грамматикой. Однако перед лексическим анализатором стоит более сложная задача: он должен сам выделить в исходном тексте цепочку символов, представляющую лексему, а также преобразовать ее в пару (тип_лексемы, указатель_на_информацию_о_ней). Для того, чтобы решить эту задачу, опираясь на способ анализа с помощью диаграммы состояний, введем на дугах дополнительный вид пометок - пометки-действия. Теперь каждая дуга в ДС может выглядеть так:

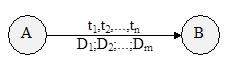
Смысл t_i прежний - если в состоянии A очередной анализируемый символ совпадает с t_i для какого-либо i = 1, 2,... n, то осуществляется переход в состояние B; при этом необходимо выполнить действия D₁, D₂,...,D_m.

Дата добавления: 2015-06-27