Принцип рекурсии в правилах грамматики

Особенность формальных грамматик в том, что они позволяют определить бес­конечное множество цепочек языка с помощью конечного набора правил (конеч­но, множество цепочек языка тоже может быть конечным, но даже для простых реальных языков это условие обычно не выполняется). Приведенная выше в примере грамматика для целых десятичных чисел со знаком определяет беско­нечное множество целых чисел с помощью 15 правил.

Возможность пользоваться конечным набором правил достигается в такой фор­ме записи грамматики за счет рекурсивных правил. Рекурсия в правилах грам­матики выражается в том, что один из нетерминальных символов определяется сам через себя. Рекурсия может быть непосредственной (явной) — тогда символ определяется сам через себя в одном правиле, либо косвенной (неявной) — тогда то же самое происходит через цепочку правил.

В рассмотренной выше грамматике G непосредственная рекурсия присутствует в правиле: <чс>-»<чс><цифра>, а в эквивалентной ей грамматике G' — в правиле: T-VTF.

Чтобы рекурсия не была бесконечной, для участвующего в ней нетерминального символа грамматики должны существовать также и другие правила, которые оп­ределяют его, минуя самого себя, и позволяют избежать бесконечного рекурсив­ного определения (в противном случае этот символ в грамматике был бы просто не нужен). Такими правилами являются <чс>-»<цифра> — в грамматике G и T->F -в грамматике G'.

В теории формальных языков более ничего сказать о рекурсии нельзя. Но, чтобы полнее понять смысл рекурсии, можно прибегнуть к семантике языка — в рас­смотренном выше примере это язык целых десятичных чисел со знаком. Рас­смотрим его смысл.

Определение грамматики. Форма ьэкуса—маура «ЗО /

Если попытаться дать определение тому, что же является числом, то начать мож­но с того, что любая цифра сама по себе есть число. Далее можно заметить, что _любые две цифры — это тоже число, затем — три цифры и т. д. Если строить определение числа таким методом, то оно никогда не будет закончено (в матема­тике разрядность числа ничем не ограничена). Однако можно заметить, что каж­дый раз, порождая новое число, мы просто дописываем едифру справа (посколь­ку привыкли писать слева направо) к уже написанному ряду цифр. А этот ряд цифр, начиная от одной цифры, тоже в свою очередь является числом. Тогда определение для понятия «число» можно построить таким образом: «число — это любая цифра, либо другое число, к которому справа дописана любая цифра». Именно это и составляет основу правил грамматик G и G' и отражено во второй строке правил в правилах <чс>—><цифра> [ <чс><цифра> и Т—>F | TF. Другие правила в этих грамматиках позволяют добавить к числу знак (первая строка правил) и дают определение понятию «цифра» (третья строка правил). Они элементарны и не требуют пояснений.

Принцип рекурсии (иногда его называют «принцип итерации», что не меняет сути) — важное понятие в представлении о формальных грамматиках. Так или иначе, явно или неявно рекурсия всегда присутствует в грамматиках любых ре­альных языков программирования. Именно она позволяет строить бесконечное множество цепочек языка, и говорить об их порождении невозможно без пони­мания принципа рекурсии. Как правило, в грамматике реального язык? програм­мирования содержится не одно, а целое множество правил, построенных с помо­щью рекурсии.

Другие способы задания грамматик

Форма Бэкуса—Наура — удобный с формальной точки зрения, но не всегда дос­тупный для понимания способ записи формальных грамматик. Рекурсивные определения хороши для формального анализа цепочек языка, но не удобны с точки зрения человека. Например, то, что правила <чс>-><цифра> | <чс><цифра> отражают возможность для построения числа дописывать справа любое число цифр, начиная от одной, неочевидно и требует дополнительного пояснения.

Но при создании языка программирования важно, чтобы его грамматику пони­мали не только те, кому предстоит создавать компиляторы для этого языка, но и пользователи языка — будущие разработчики программ. Поэтому существуют Другие способы описания правил формальных грамматик, которые ориентирова­ны на большую понятность человеку.

Далее рассмотрим два наиболее распространенных из этих способов: запись пра­вил грамматик с использованием метасимволов и запись правил грамматик в графическом виде.

Запись правил грамматик

с использованием метасимволов

Запись правил грамматик с использованием метасимволов предполагает, что в строке правила грамматики могут встречаться специальные символы — мета-

358 Глава 9. Формальные языки и грамматики

символы, — которые имеют особый смысл и трактуются специальным образом. В качестве таких метасимволов чаще всего используются следующие символы: () (круглые скобки), [] (квадратные скобки), {} (фигурные скобки), «,» (запя­тая) и "" (кавычки). Эти метасимволы имеют следующий смысл:

□ круглые скобки означают, что из всех перечисленных внутри них цепочек
символов в данном месте правила грамматики может стоять только одна це­
почка;

□ квадратные скобки означают, что указанная в них цепочка может встречать­
ся, а может и не встречаться в данном месте правила грамматики (то есть мо­
жет быть в нем один раз или ни одного раза);

□ фигурные скобки означают, что указанная внутри них цепочка может не встре­
чаться в данном месте правила грамматики ни одного раза, встречаться один
раз или сколь угодно много раз;

□ запятая служит для того, чтобы разделять цепочки символов внутри круглых
скобок;

□ кавычки используются в тех случаях, когда один из метасимволов нужно
включить в цепочку обычным образом — то есть когда одна из скобок или за­
пятая должны присутствовать в цепочке символов языка (если саму кавычку
нужно включить в цепочку символов, то ее надо повторить дважды — этот
принцип знаком разработчикам программ).

Вот как должны выглядеть правила рассмотренной выше грамматики G, если их записать с использованием метасимволов:

<число> -» [(+.-)]<цифра>{<цифра>}

<цифра> ->0|1|2|3|4|5|6|7|8|9

Вторая строка правил не нуждается в комментариях, а первое правило читается так: «число есть цепочка символов, которая может начинаться с символов + или -, должна содержать дальше одну цифру, за которой может следовать последова­тельность из любого количества цифр». В отличие от формы Бэкуса—Наура, в форме записи с помощью метасимволов, как видно, во-первых, убран из грам­матики малопонятный нетерминальный символ <чс>, а во-вторых — удалось пол­ностью исключить рекурсию. Грамматика в итоге стала более понятной.

Форма записи правил с использованием метасимволов — это удобный и понят­ный способ представления правил грамматик. Она во многих случаях позволяет полностью избавиться от рекурсии, заменив ее символом итерации {} (фигур­ные скобки). Как будет понятно из дальнейшего материала, эта форма наиболее употребительна для одного из типов грамматик — регулярных грамматик.

Запись правил грамматик в графическом виде

При записи правил в графическом виде вся грамматика представляется в форме набора специальным образом построенных диаграмм. Эта форма была предло­жена при описании грамматики языка Pascal, а затем она получила широкое рас­пространение в литературе. Она доступна не для всех типов грамматик, а только

Определение грамматики. Форма Бэкуса—Наура 359

для контекстно-свободных и регулярных типов, но этого достаточно, чтобы ее можно было использовать для описания грамматик известных языков програм­мирования.

В такой форме записи каждому нетерминальному символу грамматики соответ­ствует диаграмма, построенная в виде направленного графа. Граф имеет следую­щие типы вершин:

□ точка входа (на диаграмме никак не обозначена, из нее просто начинается
входная дуга графа);

□ нетерминальный символ (на диаграмме обозначается прямоугольником, в ко­
торый вписано обозначение символа);

□ цепочка терминальных символов (на диаграмме обозначается овалом, кругом
или прямоугольником с закругленными краями, внутрь которого вписана це­
почка);

□ узловая точка (на диаграмме обозначается жирной точкой или закрашенным
кружком);

□ точка выхода (никак не обозначена, в нее просто входит выходная дуга графа).

Каждая диаграмма имеет только одну точку входа и одну точку выхода, но сколь­ко угодно вершин других трех типов. Вершины соединяются между собой на­правленными дугами графа (линиями со стрелками). Из входной точки дуги могут только выходить, а во входную точку — только входить. В остальные вер­шины дуги могут как входить, так и выходить (в правильно построенной грам­матике каждая вершина должна иметь как минимум один вход и как минимум один выход).

Чтобы построить цепочку символов, соответствующую какому-либо нетерми­нальному символу грамматики, надо рассмотреть диаграмму для этого символа. Тогда, начав движение от точки входа, надо двигаться по дугам графа диаграммы через любые вершины вплоть до точки выхода. При этом, проходя через верши­ну, обозначенную нетерминальным символом, этот символ следует поместить в результирующую цепочку. При прохождении через вершину, обозначенную цепочкой терминальных символов, эти символы также следует поместить в ре­зультирующую цепочку. При прохождении через узловые точки диаграммы над результирующей цепочкой никаких действий выполнять не надо. Через любую вершину графа диаграммы, в зависимости от возможного пути движения, можно пройти один раз, ни разу или сколь угодно много раз. Как только мы попадем в точку выхода диаграммы, построение результирующей цепочки закончено.

Результирующая цепочка, в свою очередь, может содержать нетерминальные символы. Чтобы заменить их на цепочки терминальных символов, нужно, опять же, рассматривать соответствующие им диаграммы. И так до тех пор, пока в це­почке не останутся только терминальные символы. Очевидно, что для того, что­бы построить цепочку символов заданного языка, надо начать рассмотрение с Диаграммы целевого символа грамматики.

Это удобный способ описания правил грамматик, оперирующий образами, а по­тому ориентированный исключительно на людей. Даже простое изложение его основных принципов здесь оказалось довольно громоздким, в то время как суть

зеи

Глава 9. формальные языки и i рамматики

способа довольно проста. Это можно легко заметить, если посмотреть на описа­ние понятия «число» из грамматики G с помощью диаграмм на рис. 9.1.

Число:

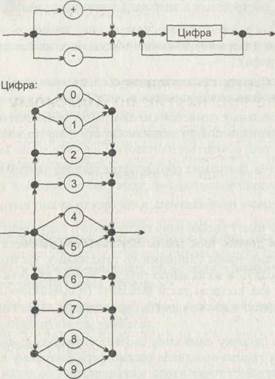
Рис. 9.1. Графическое представление грамматики целых десятичных чисел со знаком: вверху — для понятия «число»; внизу — для понятия «цифра»

Как уже было сказано выше, данный способ в основном применяется в литерату­ре при изложении грамматик языков программирования. Для пользователей — разработчиков программ — он удобен, но практического применения в компиля­торах пока не имеет.

Классификация языков и грамматик

Выше уже упоминались различные типы грамматик, но не было указано, как и по какому принципу они подразделяются на типы. Для человека языки быва­ют простые и сложные, но это сугубо субъективное мнение, которое зачастую за­висит от личности человека.

Для компиляторов языки также можно разделить на простые и сложные, но в данном случае существуют жесткие критерии для этого разделения. Как будет показано далее, от того, к какому типу относится тот или иной язык программи-

рования, зависит сложность распознавателя для этого языка. Чем сложнее язык, тем выше вычислительные затраты компилятора на анализ цепочек исходной программы, написанной на этом языке, а следовательно, сложнее сам компиля­тор и его структура. Для некоторых типов языков в принципе невозможно по­строить компилятор, который бы анализировал исходные тексты на этих языках за приемлемое время на основе ограниченных вычислительных ресурсов (имен­но поэтому до сих пор невозможно создавать программы на естественных язы­ках, например на русском или английском).

Классификация грамматик.

Дата добавления: 2015-06-27