Логическая модель представления знаний

В основе модели такого вида лежит формальная система, задаваемая: M = <T, P, A, B>, где

Т – множество базовых элементов из выбранной предметной области (алфавит системы);

Р – множество синтаксических правил (операций, связок) с помощью которых образуются синтаксически правильные выражения;

А – аксиомы (не доказуемые, не противоречивые утверждения данной формальной системы);

В – правила вывода. Применяя правила вывода к элементам А, можно получить новые синтаксически правильные выражения, выводимые в данной системе.

Проблема логического представления знаний: можно создать гипотезу, которая будет тождественно истинна на всех переменных, входящих в эту систему и которая будет доказуема.

Запись фраз (Таблица 12).

Таблица 12 Запись фраз в виде логических формул

Обычный язык	Логический язык предметной области	Формальный язык
Горький написал «Мать»	Писать (Горький, Мать)	Р(а, b) а – определено на множестве писа-телей, в – на мно-жестве книг.
Мать Ивана замужем за отцом Ивана.	Супружество [Отец (Иван), мать (Иван)]	Q[f(a), φ(a)] Q – предикат супружество, f – отец, a – Иван, φ – мать.
Этот дом желтый.	1. Дом (Желтый) 2. Цвет (Дом, Желтый) 3. Значение цвета (Цвет,Дом, Желтый).	1. D(y) 2. C(d, y) 3. Z(c, d, y)

Нельзя выбрать однозначное описание на формальном языке.

Недостатком логического представления знаний является неоднозначность перевода с обычного языка на логический язык предметной области. Этот выбор зависит от задачи.

Запись сложных фраз (Таблица 13).

Таблица 13 Запись сложных фраз

Обычный язык	Логический язык предметной области	Формальный язык
Слава любит Машу и слава любит Дашу.	[Любит (Слава, Маша) ^ Любит (Слава, Даша)]	[Р (а, b) ^ Р (а, с)]
Олег любит играть в волейбол в центре поля и около сетки.	[Любит играть (Олег, Центр) ^ Любит играть (Олег, Сетка)]	[Р (а, b) ^ Р (а, с)]
Если машина принадлежит Олегу, то она зеленая.	[Владеть (Олег, Машина) → Цвет (Машина, Зеленый)]	Р (а, b) → Q(b, c)
Горький не написал «тихий Дон»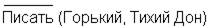

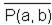
Запись утверждений

Таблица 14 Запись утверждений

Обычный язык	Логический язык предметной области	Формальный язык
Все слоны серые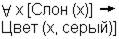
Существует человек, который написал «Тихий Дон»		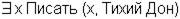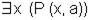Р – предикат Писать; х – человек; а – Тихий дон.
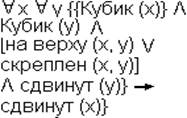
Нильс Нильсон «Мир Кубиков»: Все кубики, которые были сдвинуты или скреплены с кубиками, которые сдвигали, так же были сдвинуты.		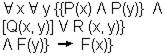Р – предикат кубика; Q – на верху; R – скреплен; F - действия

Описание ситуаций.

На (С, А) ^

На столе (А) ^

На столе (В) ^ ФАКТЫ

Свободный (С) ^

Свободный (В)

Р (с, а) ^ Q (a) ^

Q (b) ^ R (c) ^

R (b)

Аксиома:

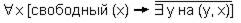
Основная идея: вводятся некие факты в формальном виде и доказывается их истинность или ложность.

Дата добавления: 2015-06-27