Задачи, решаемые с помощью графов

1. Задача поиска наикратчайшего пути на графе.

Задан ориентированный граф.

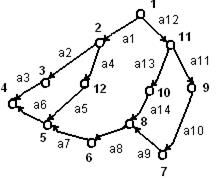
Рис.28. Ориентированный граф

Решение любой задачи оптимизации: f (x₁,….,x_n) → min / max

M (1,5) ∑ α _i = min (i = 1,…,n)

Задача решается методом «ветвей и границ».

2. Транспортная задача.

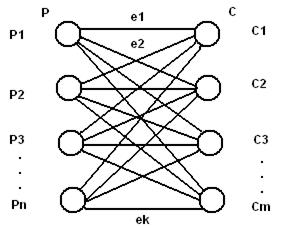
Рис.29. Транспортная сеть

Р – производители некоторой продукции;

С – потребители продукции;

е₁, е₂,…,е_к – маршруты;

к = m*n

Есть некий заказ Р, который состоит из подзаказов р₁, р₂, …, р₃ и объема продукции, которую необходимо потребить.

Р = ∑р_i (i = 1,…,n)

C = ∑c_j (j = 1,…,m)

P = C

Ограничения: Каждый маршрут имеет свой вес, свои затраты Se₁,…,Se_k и ограничения на пропускную способность. Se₁d₁,…,Se_kd_k

Необходимо найти маршруты от производителей к потребителям, чтобы

∑Se_l → min (e = 1,…,k)

Алгоритм Форда-Фолкерсона.

3. Задача о назначении (задача коммивояжера).

Есть несколько городов и дороги между ними. Найти маршрут коммивояжера, чтобы он посетил каждый город только 1 раз.

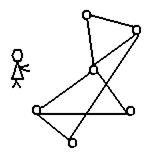
Рис.30. Сеть коммивояжёра

Это задача целочисленного программирования (оптимизации). Особенность: задачи легко ставятся, но тяжело решаются.

4. Задача о назначении работ.

Рис.31. Станки и детали

D1 (t₁`, t<sub>2</sub>`, t₃`, t<sub>4</sub>`, t₅`)

D2 (t₁``, t<sub>2</sub>``, t₃``, t<sub>4</sub>``, t₅``)

Есть n станков и n деталей. Каждая деталь должна обрабатываться на 5-ти станках, причем время обработки разное для каждой детали.

t₁`, t<sub>2</sub>`, t₃`, t<sub>4</sub>`, t₅` – время обработки детали 1 на 1-ом,…,5-ом станке.

t₁``, t<sub>2</sub>``, t₃``, t<sub>4</sub>``, t₅``- время обработки детали 2 на 1-ом,…,5-ом станке.

В какой последовательности запустить детали на обработку, чтобы время выполнения заказов было минимальным.

Дата добавления: 2015-06-27