Критерий Найквиста

Теория генетического поля формирования Эго.

Ее значение для патологии......................................................... 111

Созревание и развитие.................................................................114

Самый ранний уровень психологического развития................115

Появление предшественника либидинозного объекта

и его значение...............................................................................117

Экскурс в эмбриологию...............................................................122

Первый организатор психики.....................................................125

Второй организатор психики......................................................126

Зависимое развитие......................................................................128

Третий организатор психики......................!................................130

Второй экскурс в эмбриологию...................................................132

Дифференциация, интеграция и кумуляция.............................138

Дисбаланс развития......................................................................141

Критические периоды..................................................................142

Синхронность и интеграция........................................................147

Точки фиксации...........................................................................148

Выводы для терапии и профилактики........................................153

Резюме...........................................................................................155

Библиография...............................................................................156

Научное издание Рене А. Шпиц

Психоанализ раннего детского возраста

Художник П.П. Ефремов

Компьютерная верстка Ю.В. Балабанов

Корректор Л.Н. Гагулина

Лицензия ИД №01018 от 21 февраля 2000 г.

Издательство «ПЕР СЭ»

129366, Москва, ул.Ярославская, 13, к.120

тел/факс: [phone]

e-mail: [e-mail]

Лицензия ЛР№ 071351 от 23.10.96 Издательство Фонда поддержки науки и образования

«Университетская книга» Санкт-Петербург, ул. Моисеенко, д. 10

Налоговая льгота — общероссийский классификатор продукции ОК-005-093, том 2; 953000 — книги, брошюры

Подписано в печать 15.01.2001 Формат 60x90/16 Печать офсетная. Гарнитура Тайме. Бумага офсетная.

Усл.печ.л. 10 Тираж 3000 экз. Заказ № 28т. Типография ФГУП «Полиграфические ресурсы»

Если разомкнутая система устойчива (m _раз=0), то годограф Найквиста (годограф W _раз (jw)) для устойчивости замкнутой системы не должен охватывать точку с координатами (-1;0), иначе, если годограф охватывает эту точку, то система не устойчива. Если годограф разомкнутой системы проходит через точку (-1;0), то замкнутая система на границе устойчивости.

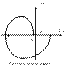
можно сформулировать критерий Найквиста в другом виде:

Если разомкнутая система неустойчива и имеет m правых корней, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста охватывал в положительном направлении 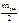раз.

Введем обозначения: n1 – количество положительных переходов (от -1 к -¥) отрезка от -1 до -¥;

n2 – количество отрицательных переходов отрезка от -1 до -¥.

Второй вариант критерия Найквиста:

Если разомкнутая система не устойчива и имеет m правых корней, то для устойчивости замкнутой системы необходимо и достаточно, чтобы разность положительных и отрицательных переходов годографа Найквиста через отрезок (-1;--¥) равнялась n1-n2=m/2.

A(ω_π) < 1

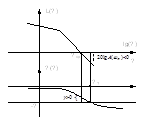
L(ω) = 20lg A(ω) Если L(ω) = 0, то A(ω) = 1, т.е. A(ω) = A(ω_ср)

Значение a в неявном виде, обходя процедуру логарифмирования:

a = 1 – A(ω_π), будет > 0.

Если a > 0 и γ > 0, то, следовательно, система устойчива и ω_ср < ω_π

20lg A(ω_π) > 0, следовательно, A(ω_π) > 1, и следовательно, a = 1 – A(ω_п) < 0.

Если a < 0 и γ < 0, то система неустойчива и ω_π < ω_ср

Система на границе устойчивости:

По годографу можно определить и запас, и параметры.

Чтобы сделать систему устойчивой:

· нужно уменьшить коэффициенты

(Недостатки: уменьшение коэффициентов равносильно снижению чувствительности и увеличению помех, следовательно, происходит потеря в точности; Достоинство: уменьшение мощности)

· у нас есть хотя бы интегратор I звена, следовательно, проявляются инерционные свойства. Мы могли бы поставить фильтр в районе ω_ср. Это позволит нам «приподнять» кривую:

Стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости. Колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости

Пусть есть устойчивая система. При изменении параметров этой системы возникает движение корней следовательно, возникает незатухающий режим колебаний. Чтобы эти колебания не возникали, надо «отделить» корни от мнимой оси. Значит, значения параметров удалить от граничных значений.

По критерию Гурвица:

Пусть есть некоторое характеристическое уравнение G(p) = 0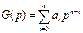

a_i > 0, и Δ_i > 0, i = 1,…,n

Система находится на границе устойчивости, если Δ_n = a_n*Δ_n-1 = 0, следовательно: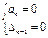

Если нам нужно удалиться от этой границы на определенную величину: Δ_i > A_i, где A_i – набор числовых значений запасов.

По Гурвицу неудобно находить A_i. Пусть наше характеристическое уравнение имеет вид:

a₀p³ + a₁p² + a₂p +a₃ = 0

Условие по Гурвицу можно записать так (для нашего уравнения):

a₁a₂ – a₀a₃ > A₂, можно найти a₀. Опытным путем можно найти соответствующие параметры.

По критерию Раусса – аналогично.

По критерию Найквиста.

где γ – запас устойчивости по фазе; a – запас устойчивости по модулю.

Если бы годограф проходил через точку (-1; 0), то система была бы на границе устойчивости. В этом случае ω_ср = ω_п

Для устойчивой системы:

γ = π + Φ(ω_ср), где Φ(ω_ср) = Arg w(jω) при ω = ω_ср

В нашем случае:

γ = 180 – 150 = +30⁰ > 0, т.е. получили положительный запас по фазе.

Введем запас устойчивости по модулю:

a = 1 – A(ω_п). Эта величина должна быть > 0.

A(ω_п) = ׀W(jω)׀, где ω = ω_п a > 0;

γ всегда измеряется от уровня – π.

Годограф неустойчивой системы:

Для нашего случая: γ = π + Φ(ω_ср) = 180 – 240 = – 60⁰ < 0

γ < 0, т.е. запас по фазе отрицательный, следовательно, не может быть положительным и запас по модулю. a = 1 – А(ω_п)

a = 1 – 1,4 = – 0,4 < 0, следовательно, отрицательный запас модулю.

Под стабилизацией системы будем понимать серию мероприятий, которые обеспечивают устойчивость системы.

Методы:

· параметрическая стабилизация (изменение параметров системы)

1) параметры характеристического уравнения а_i

2) Запасы устойчивости

3) Области устойчивости в пространстве параметров

· структурные методы стабилизации

это методы, которые обеспечивают условие устойчивости за счет изменения структуры САР.

1) последовательное стабилизирующее устройство;

2) стабилизация обратной связи

Дата добавления: 2015-06-27