Функции активации

Функции активации (передаточные функции) нейрона могут иметь самые различные выражения. Как правило, функция активации 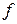принадлежит классу сигмоидных функций с аргументом 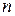и выходом .

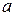Рассмотрим три наиболее часто используемые функции активации:

1) единичная функция активации с жесткими ограничениями; она описывается соотношением

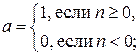
график единичной функции активации с жесткими ограничениями и ее условное обозначение представлены на рис. 1.2.

функция активации с жесткими ограничениями реализована в виде М-файла hardlim в пакете расширения Neural Network Toolbox системы MATLAB;

2) линейная функция активации; она описывается соотношением

,

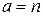а ее график и условное обозначение представлены на рис. 1.3;

в пакете расширения Neural Network Toolbox линейная функция активации реализована в виде М-файла purelin;

3) логистическая функция активации; она описывается соотношением

,

а ее график и условное обозначение представлены на рис. 1.4;

эта функция принадлежит классу сигмоидных функций, ее аргумент может принимать любое значение от до , а выход изменяется в диапазоне от 0 до 1;

в пакете расширения Neural Network Toolbox логистическая функция активации реализована в виде М-файла logsig; благодаря свойству дифференцируемости эта функция часто используется в сетях с обучением на основе метода обратного распространения ошибки.

Символы, заключенные в квадрат, в правых верхних углах графиков (см. рис. 1.2 – 1.4), характеризуют функции активации. Эти обозначения будут использованы при изображении структурных схем нейронных сетей.

В пакете расширения Neural Network Toolbox есть и другие функции активации. Кроме того, пользователь может создавать свои собственные функции с помощью языка программирования MATLAB.

Нейрон с векторным входом

На рис. 1.5 изображена схема нейрона с одним векторным входом 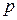, состоящим из элементов , , 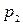…, 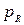. Здесь каждый элемент входа умножается на весовые коэффициенты , , 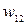…, соответственно, и взвешенные значения подаются на вход сумматора. Их сумма равна скалярному произведению век­тора весовых коэффициентов на вектор входа .

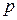Нейрон имеет смещение 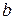, которое суммируется с взвешенной суммой входов. Результирующая сумма 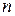определяется в соответствии с выражением

и является аргументом функции активации 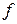. В нотации языка программирования MATLAB это выражение записывается следующим образом:

n = W*p + b.

Схема нейрона, изображенная на рис. 1.5, содержит много лишних деталей. При рассмотрении нейронных сетей, состоящих из большого числа нейронов, будет использоваться укрупненная струк­турная схема нейрона (рис. 1.6).

Вход нейрона изображается в виде темной вертикальной черты, под которой указывается количество элементов входа. Размерность входа 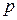указывается под стрелкой, исходящей от входа (на рис. 1.6 она обозначена 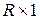). Вектор входа 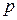умножается на вектор-строку размерности 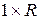. Как и прежде, константа 1 рассматривается как вход, который умножается на скалярное смещение 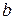. Входом 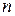функции активации 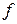нейрона является сумма скалярного произведения 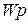и смещения 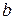. Эта сумма преобразуется функцией активации 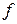, на выходе которой образуется величина 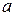, являющаяся в данном случае скалярной.

Структурная схема, изображенная на рис. 1.6, называется слоем нейронной сети. Слой характеризуется матрицей весовых коэффициентов , смещением 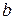, операциями умножения 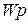и суммирования , а также функцией активации 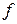. Вектор входов 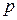обычно не включается в характеристики слоя.

Каждый раз, когда используется сокращенное обозначение нейронной сети, размерности матриц указываются под обозначениями соответствующих переменных. Подобная система обозначений поясняет строение нейронной сети и связанную с ней алгебру матриц.

На укрупненной структурной схеме для обозначения типа функции активации 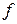иногда применяются специальные графические символы наподобие тех, что изображены на рис. 1.2 – 1.4.

Практические задания

Пример 1.1. Для функции активации с жесткими ограничениями hardlim и ее производной dhardlim, которые определяются соотношениями

,

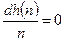выполнить следующие действия:

1. Вывести на экран информацию о функциях hardlim и dhardlim, выполнив из командной строки MATLAB следующие команды:

name = hardlim('name') % наименование функции;
dname = hardlim('deriv') % наименование производной;
inrange = hardlim('active') % диапазон входа;
outrange = hardlim('output') % диапазон выхода;

В результате выполнения в окне Command Window отобразятся следующие значения:

name =
Hard Limit

dname =
dhardlim

inrange =
0 0

outrange =
0 1

2. Построить графики функций hardlim и dhardlim, выполнив из командной строки MATLAB следующие команды:

n = -5:0.01:5; % диапазон изменения аргумента;
a = hardlim(n); % вычисление функции;
da = dhardlim(n); % вычисление производной;
plot(n,a,'r',n,da,'c') % построение графиков;
grid on % отображение сетки;

В результате выполнения откроется окно Figure No. 1, в котором будут отображены два графика – график функции hardlim, изображенный линией красного цвета, и график производной dhardlim, изображенный линией зеленого цвета (рис. 1.7).

3. Определить вектор 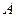выход функции активации и вектор выхода ее производной для слоя из трех нейронов, с вектором входа 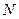, состоящим из трех элементов. Для этого нужно выполнить из командной строки MATLAB следующие команды:

N = [-0.7; 0.0; 0.8]; % вектор входа
A = hardlim(N) % вектор выхода функции активации;
dA_dN = dhardlim(N,A) % вектор выхода производной.

В результате выполнения в окне Command Window отобразятся следующие значения:

A =
0
1
1

dA_dN =
0
0
0

Рис. 1.7. Графики функции активации hardlim и ее производной dhardlim

4. Последовательность команд, которые были введены в командную строку MATLAB при выполнении пп. 1 – 3 примера, оформить в виде файла-сценария (со всеми комментариями) и сохранить в текущей папке под именем hardlimfile.m. Проверить работоспособность созданного файла-сценария.

Упражнение 1.1. Выполнить задания, аналогичные тем, что были выполнены в примере 1.1, для функций активации, представленных в табл. 1.1. Реализацию файлов-сценариев проводить на основе файла hardlimfile.m, созданного при выполнении примера 1.1. При задании входных параметров и 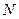охватить всевозможные «однородные фрагменты» из области определения функции активации.

Пример 1.2. Для конкурирующей функции активации compet, используемой для формирования вероятностных и самоорганизующихся нейронных сетей, выполнить следующие действия:

1. Вывести на экран информацию о функции compet, выполнив из командной строки MATLAB следующие команды:

name = compet('name') % наименование функции;
dname = compet('deriv') % наименование производной;
inrange = compet('active') % диапазон входа;
outrange = compet('output') % диапазон выхода;

Таблица 1.1

Дата добавления: 2015-06-27