Расчетные выражения для определения местных потерь напора

Наиболее часто местные потери напора hj определяются по основному выражению

(формула Ю. Вейсбаха) (6.26)

где ξ_i — коэффициент местного сопротивления (безразмерная ве­личина); v — средняя скорость потока; g — ускорение свободного падения. Как видно, местные потери определяются в долях (ча­стях) скоростного напора и пропорциональны этому скоростному напору. В (6.26) средняя скорость принимается, как правило, за местным сопротивлением. Если по каким-либо причинам при­нимается скорость перед сопротивлением, то это должно огова­риваться. Для части видов местных сопротивлений скорости до и после препятствий одинаковы (например, при повороте трубо­провода постоянного диаметра).

Коэффициенты ξ_i для абсолютного большинства местных со­противлений определяются по данным опытов. Теоретическое опре­деление ξ_i затруднено ввиду сложности явлений, происходящих в зонах местных препятствий. Значения ξ_i определены теоретиче­ски только для отдельных простейших видов местных сопротив­лений. В опытах значения ξ_i вычисляются по формуле (6.26), в которой hj представляет собой разность гидродинамических напоров до и после сопротивления. Так как hj = Δρj/γ, где Dpj— поте­ри давления на данном сопротивлении, γ — удельный вес, то из {6.26) следует также расчетное выражение в виде 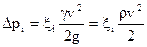(6.27)

Иногда местные потери напора представляются путевыми по­терями на некоторой эквивалентной длине l_э прямолинейного тру­бопровода. При этом путевые потери напора на длине l_э трубопро­вода равны потерям на данном местном сопротивлении. Сравни­вая формулу (6.26) с формулой для путевых потерь напора (6.11) 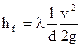, видим, что коэффициент ξ_i можно представить 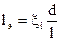(6.28)

Эквивалентная длина l_э есть такая длина участка прямолиней­ного трубопровода данного диаметра, на котором путевые потери напора равны местным потерям от данного местного сопротивле­ния. Таким образом, действительная длина трубопровода увели­чивается на эквивалентную длину. В общем случае эквивалент­ная длина зависит от видов местных сопротивлений, диаметра тру­бопровода, а также от тех же факторов, что и λ (от чисел Рейнольдса и шероховатости).

Зависимости коэффициентов местных сопротивлений от чисел Рейнольдса и режимов движения

При развитом турбулентном режиме движения, т. е. в области квадратичного сопротивления, численные значения коэффициентов ξ_i постоянные и зависят только от конструкции местного сопро­тивления (т. е. от геометрической формы области жидкости в районе местного сопротивления). При развитом турбулентном дви­жении значения ξ_i практически не зависят от чисел Рейнольдса, т. е. от вязкости жидкости и скоростей движения. Именно в обла­сти квадратичного сопротивления гидравлика местных сопротив­лений наиболее исследована, а значения коэффициентов ξ_i для разнообразных местных сопротивлений приводятся в справочной литературе.

При ламинарном режиме движения значения коэффициентов местных сопротивлений ξ_i зависят как от видов местных сопротив­лений (геометрической формы потока в зонах местных сопротив­лений), так и от чисел Рейнольдса, т. е. от вязкости движущейся среды и ее скорости движения. При ламинарном режиме движе­ния поток плавно обтекает поверхности местных сопротивлений, не возникает вихреобразований и отрывов потоков от границ, но при этом линии тока существенно искривляются. Соседние струй­ки имеют значительные относительные скорости, и, следовательно, возникают касательные напряжения, обусловливаемые силами вязкости. Последние делают наибольший вклад в местные потери напора. Важно отметить, что с увеличением Re значения ξ_i умень­шаются (значения ξ_i обратно пропорциональны Re). При лами­нарном режиме движения и малых числах Re коэффициент (6.29)

где Aj — численный коэффициент, зависящий от вида местного сопротивления. В целом вопрос об определении ξ_i при ламинар­ном режиме движения исследован недостаточно. Важно иметь в виду, что при ламинарном режиме численные значения коэффи­циентов ξ_i больше, чем при турбулентном режиме в аналогич­ных условиях.

В переходной области от ламинарного к турбулентному дви­жению значения ξ_i зависят от видов местных сопротивлений, чисел Re (т. е. от вязкости) и шероховатости границ. С увеличением чисел Re кроме потерь на вязкое трение добавляются потери на вихреобразования и отрывы потока от границ. Здесь коэффициен­ты ξ_i определяются по данным опытов и не всегда имеют посто­янные численные значения, а представляются графическими за­висимостями.

Для трубопроводов как в переходной области, так и в зоне ламинарного режима рекомендуется [4] представлять 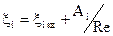(6.30)

где ξ_{i кв} — коэффициент местного сопротивления для рассматри­ваемого местного препятствия в области квадратичного сопротив­ления (значения приводятся в справочниках), Aj — опытный чис­ленный коэффициент, учитывающий особенности обтекания пре­пятствий. Численные значения входящих в формулы (6.29), (6.30) коэффициентов Аj, а также коэффициентов местных сопротивле­ний ξ_{i кв} приводятся в справочниках [16,54,55]. В табл. 6.1 поме­щены значения этих коэффициентов для некоторых видов местных сопротивлений.

Таблица 6.1

Значения коэффициентов ζj. _кв и Aj

Вид сопротивления	j KB	^Аj
Плавный поворот трубы на 90°	0,2
Резкий поворот трубы на 90°	1,2
Тройник	0.3
Задвижка, полностью открытая	0,15
Кран пробочный	0,4
Вентиль обыкновенный	4—6
Клапан шаровой

§ 6.5. ХАРАКТЕРИСТИКИ НЕКОТОРЫХ МЕСТНЫХ СОПРОТИВЛЕНИЙ, КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ СИСТЕМЫ

В рассматриваемом в данном параграфе материале, относя­щемся к отдельным видам местных сопротивлений, предполага­ется развитый турбулентный режим в области квадратичного со­противления. Движение установившееся, среда несжимаемая. Как уже отмечалось, для абсолютного большинства местных сопротив­лений значения коэффициентов ζ/ определены опытным путем (построены соответствующие таблицы, графики и др.), и только для отдельных сопротивлений простых видов определение ξ/ вы­полнено теоретически с опытной проверкой результатов. Ниже рассмотрена физическая картина и приведены рекомендации для определения коэффициентов сопротивлений только некоторых ме­стных препятствий (внезапного расширения и сужения, диффузора и конфузора, поворотов). В приложении 3 (§ П.3.2) учебника помещены рекомендации по определению коэффициентов сопро­тивлений для ряда видов местных препятствий, что необходимо для выполнения лабораторных работ, расчетно-графических уп­ражнений и курсовых работ. Наиболее полные данные о коэффи­циентах местных сопротивлений приводятся в справочниках [8, 16, 54, 55].

Внезапное расширение

Трубопроводы систем водоснабжения, теплоснабжения, венти­ляции часто в местах смены сечений включают внезапные рас­ширения (рис. 6.4, а). При этом происходит смена меньшего по площади сечения на большее. Поток из трубы меньшего диаметра по переходе сечения внезапного расширения не может сразу рас­шириться и заполнить все пространство в трубе большого диа­метра. Поток постепенно расширяется и заполняет все простран­ство трубы на некотором расстоянии от места смены сечений. Сразу за сечением с внезапным расширением в угловом кольце­вом пространстве имеется вихревая область с вакуумом, наличием воздушных пузырьков. Эту вихревую область, с другой стороны, можно называть застойной, так как жидкость в ней медленно обновляется и только частично участвует в общем движении. Средняя скорость в общем потоке после внезапного расширения уменьшается.

3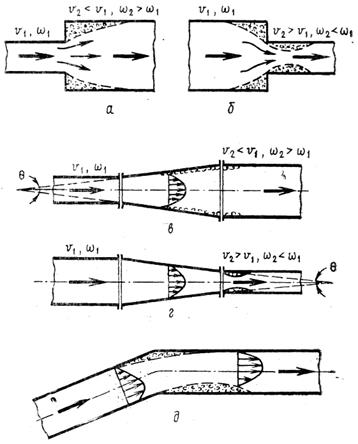

Рис. 6.4

В гидромеханике известна теорема Борда (или Борда — Карно), в соответствии с которой потери напора на внезапном рас­ширении равны скоростному напору потерянной скорости:

(6.31)

где v1 — средняя скорость до, a V₂ — после внезапного расши­рения.

Пусть ω1 — площадь живого сечения потока до, а w2— после внезапного расширения. В соответствии с уравнением неразрывности движения в гидравлической форме должно быть v1w1 = v₂w2. С учетом отмеченного (6.31) преобразуется так: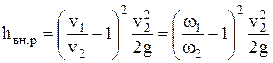

откуда окончательно 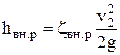(32)

Здесь ξ_ΒΗ.ρ — коэффициент сопротивления внезапного расширения. Формулы (6.31), (6.32) хорошо подтверждаются опытами при раз­витом турбулентном режиме движения. В частном случае течения из трубопровода в резервуар больших размеров нужно принять V₂->0, w2->оо· Тогда по (6.31) потери на выходе из трубопровода

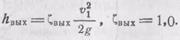
Здесь ksiвых отнесено к скорости перед внезапным расширением. Формула Борда (6.31) преобразуется также в выражение

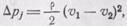(6.33)

т. е. потери давления при внезапном расширении равны, динами­ческому давлению, определенному по потерянной скорости.

Формулу (6.31) и выражение для коэффициента ζ_ΒΗ. ρ (6.32) представляют также в виде

,

где α — корректив кинетической энергии. Потери напора на выходе из трубопровода в резервуар h_вых = av1²/2g, ksi_Вых = а. Корректив а= 1,03- 1,10; при больших числах Re в квадратичной области сопротивления можно принимать α =1,0.

Внезапное сужение

При внезапном сужении происходит смена большего по площа­ди сечения на меньшее (рис. 6.4,б). Перед сечением с внезапным сужением линии тока искривляются, струя на начальном участке трубопровода меньшего диаметра сжимается, а далее расширя­ется, заполняя все сечение. Как перед, так и после сечения вне­запного сужения образуются вихревые зоны, жидкость в которых постепенно обновляется. Энергия движущейся среды расходуется на сжатие и расширение потока, вихреобразование, трение. При закруглении кромок на входе в трубу меньшего диаметра потери напора существенно уменьшаются. Потери напора h_bh. _c и коэф­фициент сопротивления местного сопротивления ζ_ΕΗ. _с определя­ются формулами:

(6.34)

Здесь второе выражение есть приближенная полуэмпирическая формула [16]. При выходе трубы из резервуара. (w1->oo, ω₂:ω1 = = 0) коэффициент сопротивления для выхода ζ_Βых = 0,5. Для опре­деления значений ζ_ΒΗ. с в справочниках [16, 54, 55] приводятся более строгие зависимости с построенными по ним таблицами. В заключение следует заметить, что при внезапном сужении потери напора всегда меньше, чем в случае внезапного расшире­ния при одинаковой геометрии перехода, скоростях и др.

Дата добавления: 2015-06-27