Вторая версия алгоритма

Простейший алгоритм

Алгоритмы вычисления квадратного корня

Рассмотрим алгоритмы вычисления целой части квадратного корня, т.е. функции y = isqrt(x) = floor(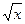), где floor ¾ функция вычисления целой части вещественного аргумента. Функцию isqrt можно представить следующей спецификацией:

isqrt(nat x: nat m) post m^2 <= x < (m + 1)^2;

Здесь “^” операция возведения в степень.

Самое простое решение задачи вычисления значения функции isqrt ¾ посредством последовательного перебора значений аргумента. Искомое значение ближе к нулю, чем к аргументу x. поэтому лучше начать с нуля. Чтобы получить программу с хвостовой рекурсией, введем следующее обобщение задачи:

sq0(nat x, k: nat m) pre k^2 <= x post m^2 <= x < (m + 1)^2;

Дополнительный аргумент k находится между нулем и искомым решением. Предикатная программа очевидна и представлена ниже:

isqrt(nat x: nat m)

{ sq0(x, 0: m) }

post m^2 <= x < (m + 1)^2;

sq0(nat x, k: nat m)

pre k^2 <= x

{ if (x < (k + 1)^2) m = k else sq0(x, k + 1: m) }

post m^2 <= x < (m + 1)^2;

Заметным недостатком алгоритма sq0 является вычисление квадрата в выражении (k + 1)^2. Между тем значение k^2 вычисляется на предыдущем шаге. С его помощью можно упростить вычисление (k + 1)^2. Рассмотрим следующую спецификацию:

sq1(nat x, k, n: nat m) pre k^2 <= x & n = k^2 post m^2 <= x < (m + 1)^2;

Дополнительный аргумент n хранит значение k^2, вычисленное на предыдущем шаге. Реализация данной идеи воплощается в следующей программе:

isqrt(nat x: nat m)

{ sq1(x, 0, 0: m) }

post m^2 <= x < (m + 1)^2;

sq1(nat x, k, n: nat m)

pre k^2 <= x & n = k^2

{ nat p = n + 2* k + 1;

if (x < p) m = k else sq1(x, k + 1, p: m)

}

post m^2 <= x < (m + 1)^2;

Построим соответствующую императивную программу для приведенной выше предикатной программы. На первом этапе трансформации предикатной программы реализуются следующие склеивания переменных.

sq1: m <- k; n <- p;

В результате склеивания получим

sq1(nat x, m, n: nat m)

{n = n + 2* k + 1;

if (x < n) m = m else sq1(x, m + 1, n: m)

}

На втором этапе реализуется замена хвостовой рекурсии циклами. Результатом проведения двух этапов трансформации является следующая программа:

isqrt(nat x: nat m)

{ sq1(x, 0, 0: m) }

sq1(nat x, m. n: nat m)

{ for (;;) {

n = n + 2* m + 1;

if (x < n) breakelse m = m + 1

}

}

На третьем этапе проведем подстановку телa определения sq1 на место вызова. Итоговая программа приведена ниже.

isqrt(nat x: nat m)

{ m = 0; nat n = 0;

for (;;) {

n = n + 2* m + 1;

if (x < n) breakelse m = m + 1

}

}

Дата добавления: 2015-06-27