
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения типовых задач
|
|
|
|
ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
Методические указания к практическим занятиям
по дисциплине «Основы дискретной математики»
для студентов дневного и заочного отделения
специальности 7.080401
«Информационные управляющие системы и технологии»
Севастополь
УДК 164.2
Высказывания, операции над высказываниями: методические указания к практическим занятиям по дисциплине «Основы дискретной математики» для студентов дневного и заочного отделения специальности 7.080401 «Информационные управляющие системы и технологии» /Сост. С.В.Доценко, Е.Н.Татарченко. – Севастополь: Изд-во СевНТУ, 2004. – 14 с.
Методические указания предназначены для проведения практических занятий по дисциплине «Основы дискретной математики». Целью методических указаний является выработка у студентов практических навыков по решению прикладных задач алгебры высказываний.
Методические указания составлены в соответствии с требованиями программы дисциплины «Основы дискретной математики» для студентов специальности 7.080401 и утверждены на заседании кафедры информационных систем, протокол № 12 от 7 июня 2004 года.
Допущено учебно-методическим центром СевНТУ в качестве методических указаний.
Рецензент Кирюхин В.В., канд.физ.-мат.наук, проф. кафедры КиВТ
СОДЕРЖАНИЕ
| 1. | Теоретический раздел.......................................... | |
| 2. | Примеры решения типовых задач................................ | |
| 3. | Задачи для упражнений........................................ | |
| Библиографический список..................................... |
Высказывание – это любое предложение какого-либо языка, содержание которого можно оценивать как истинное либо ложное.
С истинным высказыванием сопоставляется символ «и» или «t», или «1» («истина»), с ложным – «л», или «f», или «0» («ложь»). Они образуют значение истинности высказывания.
В естественных языках высказывания выражаются повествовательными предложениями. Вопросительные и восклицательные предложения, как правило, не рассматриваются в качестве высказываний. О предложениях типа « » нельзя сказать, истинно оно или ложно, до тех пор, пока на места переменных «х» и «у» не будут поставлены определенные числа. Такие предложения называются предикатами или логическими функциями высказываний.
» нельзя сказать, истинно оно или ложно, до тех пор, пока на места переменных «х» и «у» не будут поставлены определенные числа. Такие предложения называются предикатами или логическими функциями высказываний.
Предложения, не имеющие смысла в системе какого-либо языка, называются бессмысленными.
Высказывания будем обозначать строчными буквами латинского алфавита: a, b, …, x, y, z. Эти буквы могут обозначать имена определенных высказываний или же использоваться в качестве логических переменных, на места которых можно подставлять произвольные высказывания. Они могут употребляться без индексов или с индексами.
Высказывание, содержащее в качестве своих частей другие высказывания, называется составным (сложным). Если же никакая часть данного высказывания не является высказыванием, то такое высказывание называют простым (элементарным).
Составные высказывания образуются из простых при помощи логических операций. Знаки логических операций носят название логических связок.
Основные логические операции:
а) отрицание. Отрицанием  высказывания х называется высказывание истинное тогда, когда х ложно, и ложное тогда, когда х истинно. Читается «неверно, что х»;
высказывания х называется высказывание истинное тогда, когда х ложно, и ложное тогда, когда х истинно. Читается «неверно, что х»;
б) конъюнкция. Конъюнкцией (логическим произведением) высказываний х и у называется высказывание х Ù у, которое истинно тогда и только тогда, когда истинны оба эти высказывания. Читается «х и у»;
в) дизъюнкция. Дизъюнкцией (логической суммой) высказываний х и у называется высказывание х Ú у, которое истинно, когда истинно хотя бы одно из высказываний х и у. Читается «х или у»;
г) импликация. Импликацией высказываний х и у называется высказывание х ® у, которое ложно тогда и только тогда, когда х истинно, а у ложно. Читается «если х, то у». Здесь элемент х называется посылкой (условием), у – заключением (следствием);
д) эквивалентность (равнозначность). Эквивалентностью высказываний х и у называется высказывание х «у, которое истинно тогда и только тогда, когда х и у оба одновременно истинны или оба одновременно ложны. Читается «если и только если х, то у».
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Биркгоф Г. Современная прикладная алгебра/Г.Биркгоф, Т.Барти – М.: Мир, 1976. - 400 с.
2. Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов/ И.Н.Бронштейн, К.А. Семендяев - Лейпциг: Тайбнер, М.: Наука, 1981. – 718 с.
3. Горбатов В.А. Основы дискретной математики/ В.А.Горбатов. – М.: Высш. шк., 1986. – 311 с.
4. Кемени Дж. Введение в конечную математику/ Дж.Кемени, Дж. Снелл, Дж. Томпсон. – М.: Изд-во иностранной литературы, 1963. – 486 с.
5. Коршунов Ю.М. Математические основы кибернетики/Ю.Коршунов – М.: Энергия, 1972. – 376 с.
6. Кузнецов О.П. Дискретная математика для инженера/ О. Кузнецов, Г. Адельсон - Вельский. – М.: Энергоатомиздат, 1988. – 480 с.
7. Кук Д. Компьютерная математика/ Д.Кук, Г. Бейз. – М.: Наука, 1990. – 384 с.
8. Куратовский К. Теория множеств/ К.Куратовский, А.Мостовский - М.: Мир, 1970. – 416 с.
9. Ренин С.В. Основы дискретной математики/ С. В.Ренин - Новосибирск: Новосибирский электротехнический институт, 1981. – 43 с.
10. Ренин С.В. Сб. задач и упражнений по основам теории систем/ С.В.Ренин - Новосибирск: Новосибирский электротехнический институт, 1981. - 48 с.
3.42. Найдите множество истинности каждого из приведенных высказываний, изобразив его диаграммой Эйлера – Венна:
а) (x ® у) Ù х, б) (x «y) Ù x, в) (x «y) ® y, г) (x «y) Ú y, д) (x ® y) ® y,
е) (x Ú y) «y, ж) (x Ú y) ® (х Ù y).
Определите, какие из приведенных формул эквивалентны.
3.43. Составив таблицы истинности, интерпретируйте на диаграммах Эйлера-Венна формулы:
а) (y ® x) Ù z, б) ((x ® y) Ù (y ® x)) «z, в) (x Ù y) Ú z, г) (x «y) Ù z,
д) (x ® у) «z, е)  ® (y Ù z), ж) х Ù (y «z).
® (y Ù z), ж) х Ù (y «z).
3.44. Используя диаграммы Эйлера – Венна определите, какие из приведенных высказываний всегда истинны или всегда ложны:
а) p Ú  , б) p Ù
, б) p Ù  , в) p Ú (
, в) p Ú ( Ù q), г) p ® (q ® p), д) p Ù
Ù q), г) p ® (q ® p), д) p Ù 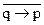 .
.
3.45. Множества истинности составных высказываний изображены в виде диаграмм Эйлера- Венна на рисунке 3.1. Постройте таблицы истинности и карты Карно этих высказываний и запишите каждое из них одной из возможных формул логики высказываний.
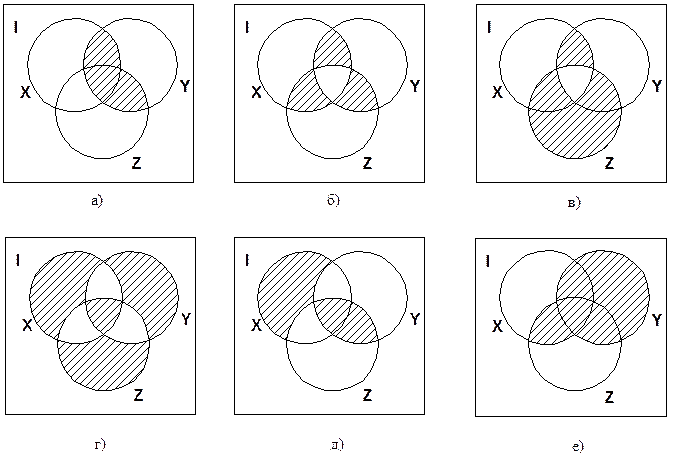
Рисунок 3.1 – Диаграммы Эйлера – Венна к заданию 3.45
3.46. Используя диаграммы Эйлера-Венна, из следующих высказываний выберите пары эквивалентных:
а)  Ú y, б)
Ú y, б) 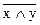 , в)
, в) 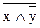 , г) х ®
, г) х ® 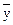 , д)
, д)  Ú
Ú 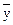 .
.
Составные высказывания, истинные независимо от истинности или ложности их составных частей, называются тождественно истинными или тавтологиями. Составные высказывания, ложные независимо от истинности или ложности их составных частей, называются тождественно ложными или абсурдными. Тождественно истинные и тождественно ложные высказывания играют важную роль в процессе логических заключений; иногда их называют законами логики.
Любая совокупность логических операций может быть представлена в виде таблиц истинности. В правой части этой таблицы записываются значения истинности составных высказываний при всех возможных комбинациях значений истинности составляющих его простых высказываний, записанных в ее левой части. При этом наборы простых высказываний, записанных в левой части таблицы будем записывать в лексикографическом порядке, т.е. в виде последовательности n-значных двоичных чисел (где n – число простых высказываний), соответствующих естественной возрастающей последовательности десятичных чисел 0, 1, 2, 3 и т.д. Например, таблица истинности для операции эквивалентности х «у имеет вид:
| х | у | х «у |
Десятичное число, которое представляется данным набором (рассматриваемым как двоичный код), называется номером этого набора. Например, набор (1110) простых высказываний (х1, х2, х3, х4) представляет собой число 0 ´ 20 + 1 ´ 21 + 1 ´ 22 + 1 ´ 23 = 14, т.е. его номер равен 14.
Одной из разновидностей таблиц истинности являются карты Карно. Примеры карт Карно для составных высказываний, включающих в себя от двух до пяти простых высказываний, приведены на рисунке 1.1:
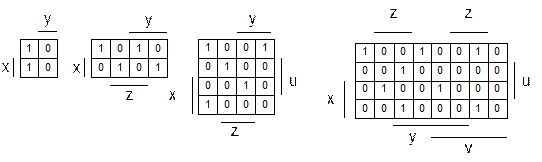
Рисунок 1.1 – Примеры карт Карно
Каждой клеточке карты Карно соответствует единственная комбинация всех исходных простых высказываний (т.е. единственный набор). Обозначения высказываний ставятся сбоку и сверху (или снизу) карты и относятся ко всей строке (или столбцу) следующих за ними клеточек, причем считается, что значения простых
высказываний равны нулю. В клеточках пишутся значения того составного высказывания, для которого составлена карта Карно.
Логические операции могут быть промоделированы комбинационными (или коммутационными, контактными) схемами, составленными из нормально разомкнутых и нормально замкнутых контактов и соединяющих их проводов. Примеры таких схем даны на рисунке 1. 2. В этих схемах горение лампочки соответствует истинному значению моделируемых ими логических операций, причем считается, что х = 1, если нажата соответствующая кнопка, и х = 0, если она не нажата.

Рисунок 1.2 – Примеры комбинационных схем
Высказывание х может быть сопоставлено с некоторым множеством Х, на элементах которого оно истинно. Таким же образом можно сопоставить с множеством Y высказывание у, с множеством Z высказывание z, и т.д. Поэтому составное высказывание может быть изображено множеством истинности на диаграммах Эйлера – Венна, как, например, на рисунке 1.3.
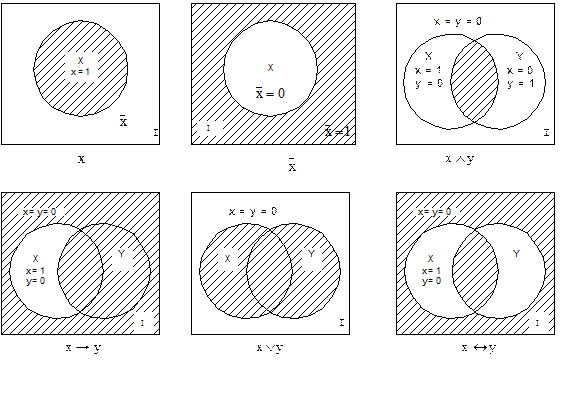
Рисунок 1.3 – Диаграммы Эйлера – Венна для некоторых высказываний
а) x «(y ® 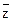 ), б) (
), б) ( Ú y) «
Ú y) «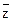 , в) (
, в) ( Ù y) «(y Ú
Ù y) «(y Ú 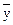 ), г) (х Ú y) ® (
), г) (х Ú y) ® (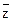 «z).
«z).
3.30. Пусть высказывания х1, х2, х3 имеют соответственно значения истинности 1, 0, 0. Не составляя полных таблиц истинности, определите значения следующих высказываний:
а) (х1 Ú х2) Ù х3, б) х1 Ù (х2 Ú х3), в) х3 ® (х1Ú х4), г) х1 ® (х3 Ú х4), д) х1 ® (х2 Ú
Ú х3), е) (х1 Ú х3) «(х2 Ù х4), ж) х1 «(х2 ® (х3 Ú х4)), з) (х1 Ù х2) ® (х3 «х4),
и) (х1 « 2) Ú х3 Ú (х4 ® х5), к) (х1 Ù х2) ® (х3 ® (х4 Ú х5)).
2) Ú х3 Ú (х4 ® х5), к) (х1 Ù х2) ® (х3 ® (х4 Ú х5)).
3.31. Известно, что p ложно, а r истинно. Используя только эту информацию, определить значения истинности:
а) p ® (q ® r), б) (p Ù q Ù r) ® r, в) (p Ù q) «(r Ú 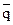 ), г) (p Ú q) Ù (r «
), г) (p Ú q) Ù (r «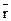 ),
),
д) (( Ú q) Ù r) «((
Ú q) Ù r) «(( Ù r) Ú (q Ù r)).
Ù r) Ú (q Ù r)).
Укажите примеры, для которых достаточно знать значение только одного высказывания – p или r.
3.32. Что можно сказать о высказывании, эквивалентном своему отрицанию?
3.33. Покажите, что высказывание (p «q) ® (p ® q) истинно, а
(p «q) ® (p Ú q) – нет.
3.34. Проверить справедливость следующих равенств:
а)  = х Ú у, б) х ® у =
= х Ú у, б) х ® у =  Ú у, в)
Ú у, в)  = х Ù у.
= х Ù у.
3.35. Известно, что х – истинно. Что можно сказать о значениях истинности следующих импликаций:
а)  ® (у Ú z), б) (
® (у Ú z), б) ( Ù у) ® z, в) (у Ù z) ® (x Ú z).
Ù у) ® z, в) (у Ù z) ® (x Ú z).
3.36. Определите значения истинности следующих выражений:
а) (1 Ù 1 Ù 1) ® 1, б) (1 Ú 1 Ú 0) ® 1, в) ((1 Ù 0) Ú ( ) ® (0 Ù 1 Ù 1), г) (1 Ú 0) ® (1 Ù 0 Ù 1), д) (((1 Ú 0) Ù 0) ® 1) Ú 0, е) (((1 ® 0) ® 1) ® 1) ® 0,
) ® (0 Ù 1 Ù 1), г) (1 Ú 0) ® (1 Ù 0 Ù 1), д) (((1 Ú 0) Ù 0) ® 1) Ú 0, е) (((1 ® 0) ® 1) ® 1) ® 0,
ж) ((0 ® 1) «0) ® (1 Ù 0), з) (1 ® 0) «( ), и) (0 Ù 1 Ù 1) ® x, к) x ® (1 Ú 1 Ú 0).
), и) (0 Ù 1 Ù 1) ® x, к) x ® (1 Ú 1 Ú 0).
3.37. Для каждой из приведенных формул определить, достаточно ли сведений о значении истинности переменных, чтобы установить значение истинности всей формулы. Если достаточно, то указать это значение. Если недостаточно, то показать, какая дополнительная информация нужна:
а) (х ® у) ® z, где z – истинно; б) х Ù (y ® z), где у – ложно; в) х Ù (y ® z), где x – истинно; г) (х Ú у) «(x Ú z), где х – ложно; д) (х Ù у) ® (x Ú z), где у – ложно;
е) (x ® y) «(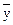 ®
®  ).
).
3.38. При помощи таблиц истинности выясните, какие из приведенных формул эквивалентны:
а) (p Ù q) ® r, б) (p Ù 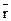 ) ® q, в) (q Ù
) ® q, в) (q Ù 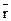 ) ®
) ®  .
.
3.39. Докажите, что отношение эквивалентности между формулами обладает свойствами рефлексивности, симметричности и транзитивности.
3.40. Найдется ли среди приведенных четырех формул такая, которая была бы эквивалентна формуле  :
:
а)  ®
® 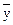 , б) х ®
, б) х ® 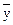 , в)
, в)  ® у, г) х Ù
® у, г) х Ù 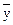 ?
?
3.41. Написать составные высказывания, соответствующие множествам
истинности: а) Х \ Y, б) Y \ X, в) Х D Y.
3.16. Построить таблицу истинности и карту Карно для каждого из следующих высказываний:
а)  , б) х Ù
, б) х Ù  , в) (х Ú у) Ú
, в) (х Ú у) Ú  , г)
, г) 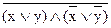 , д) x ®
, д) x ® 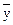 , е)
, е)  Ú у, ж) x Ù
Ú у, ж) x Ù 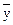 ,
,
з)  Ú
Ú 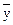 .
.
3.17. Составьте таблицу истинности и карту Карно для каждого из следующих высказываний:
а)  , б)
, б) 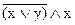 , в) x ® (у Ú z), г) (х Ú z) Ù (x ® y), д) (х Ú у) «
, в) x ® (у Ú z), г) (х Ú z) Ù (x ® y), д) (х Ú у) «
«(у Ú х), е) (х ® х) Ú (х ®  ), ж) (х Ú у) Ù z,
), ж) (х Ú у) Ù z,
з) (x ® (y ® z)) ® ((x ® y) ® (x ® z)), и)  «у, к) х ® (
«у, к) х ® ( ® у), л)
® у), л) 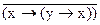 .
.
3.18. Постройте таблицы истинности и карты Карно для:
а) (х Ú у) «( ), б) (х Ù y) ®
), б) (х Ù y) ®  , в)
, в) 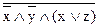 .
.
3.19. Постройте таблицы истинности и карты Карно следующих формул:
а) х ® (х ® у), б)  , в)
, в) 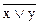 , г) (х ®
, г) (х ®  ) Ú у, д) (
) Ú у, д) ( Ù у) ® z,
Ù у) ® z,
е) х Ù у Ú  Ù у Ú
Ù у Ú  Ù
Ù 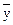 , ж) (х Ú у) «z, з) (х «у) Ù z, и) (х Ú у) Ù (
, ж) (х Ú у) «z, з) (х «у) Ù z, и) (х Ú у) Ù ( Ú
Ú 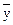 ).
).
3.20. Постройте таблицы истинности и карты Карно следующих формул:
а) (х ® у) Ù (у Ú z), б)  Ù
Ù 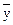 Ù z Ú
Ù z Ú  Ù y Ù
Ù y Ù 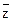 Ú x Ù y Ù z, в) (
Ú x Ù y Ù z, в) ( Ú у) Ù (у Ú z), г) (x Ú y Ú z) Ù (
Ú у) Ù (у Ú z), г) (x Ú y Ú z) Ù ( Ú y Ú z) Ù (
Ú y Ú z) Ù ( Ú y Ú
Ú y Ú 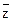 ).
).
Для каких пар этих формул имеет место отношение эквивалентности?
3.21. С помощью таблиц истинности найдите среди приведенных формул эквивалентные пары:
а) x ® (y ® z), б) (x ® y) Ù (x ® z), в) (x Ù y) ® z, г) (x ® z) Ú (y ® z),
д) х ® (у Ù z).
3.22. Из простых высказываний p, q и r постройте составное высказывание, которое было бы истинно тогда и только тогда, когда истинно только одно (безразлично какое) из высказываний p, q или r.
3.23. Высказывание х ® у истинно, а x «y - ложно. Каково значение высказывания y ® x?
3.24. Установите значения высказываний p, q, r и s в следующих четырех предложениях, первые два из которых истинны, последние два – ложны:
а) p «(4 < 5), б) q «(4 > 5), в) r «(4 < 5), г) s «(4 > 5).
3.25. Высказывание х «у истинно. Что можно сказать о значениях  «у и
«у и  «
«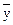 ?
?
3.26. Высказывание х «у ложно. Каковы значения истинности х «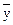 и
и  «
«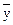 ?
?
3.27. Покажите, что высказывание (х «у) ® (х ® у) логически истинно, а
(х «у) ® (х Ú у) – нет.
3.28. Доказать, что если х истинно, то:
а) х Ú у истинно, б)  Ù у ложно, в) х Ù у эквивалентно у, г)
Ù у ложно, в) х Ù у эквивалентно у, г)  Ú у эквивалентно у.
Ú у эквивалентно у.
3.29. Известно, что х истинно, а z ложно. Определить значения истинности
2.1. Следующие утверждения являются составными высказываниями или могут быть ими интерпретированы. Найдите их простые составляющие, обозначьте буквами и запишите эти составные высказывания в символической форме:
а) Жарко и идет дождь. б) Жарко, но не очень сыро. в) Идет дождь или очень сыро. г) Андрей и Петр взобрались на холм. д) Это ни необходимо, ни желательно.
Обозначим простые высказывания:
а – «жарко», b – «идет дождь», c – «очень сыро», d – «Андрей взобрался на холм», e – «Петр взобрался на холм», f – «это необходимо», g – «это желательно».
Получим: а) a Ù b, б) a Ù 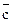 , в) b Ú c, г) d Ù e, д)
, в) b Ú c, г) d Ù e, д) 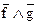 .
.
2.2. Укажите составное высказывание r, имеющее смысл «p или q, но не оба», применяя к простым высказываниям p и q связки  , Ù и Ú. Постройте таблицу истинности и карту Карно для этого высказывания.
, Ù и Ú. Постройте таблицу истинности и карту Карно для этого высказывания.
Это высказывание имеет вид p Ù 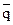 Ú
Ú  Ù q. Его таблица истинности и карта Карно
Ù q. Его таблица истинности и карта Карно
| p | q | r |
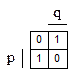
2.3. Постройте таблицы истинности и карты Карно для следующих высказываний:
а) (х ® у) Ù (у ® х), б) (х Ù у) ® х, в) у ®(х Ú у), г) (х ® у) «( Ú у).
Ú у).
Таблицы истинности построим путем нахождения таблиц истинности последовательно выполняемых логических операций:
| х | у | х ®у | у®х | х Ù у | х Ú у |  Ú у Ú у
| а) | б) | в) | г) |
Из этих таблиц истинности получим карты Карно рисунка 2.1:
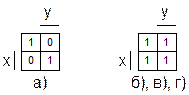
Рисунок 2.1 – Карты Карно примера 2.3
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 6015; Нарушение авторских прав?; Мы поможем в написании вашей работы!