Простой трубопровод постоянного сечения. Все трубопроводы могут быть разделены на простые и сложные

Все трубопроводы могут быть разделены на простые и сложные. Простым трубопроводом называется трубопровод без разветвлений. Простые трубопроводы могут быть соединены между собой так, что образуют последовательное, параллельное или разветвлённое соединение. Сложные трубопроводы содержат как последовательные, так и параллельные соединения или ветви разветвления.

Жидкость движется по трубопроводу благодаря тому, что её энергия в начале трубопровода больше, чем в конце.

Этот перепад (разность) уровней энергии может быть создан тем или иным способом: работой насоса, за счет разности уровней жидкости в начале и в конце трубопровода, разности давлений газа.

На практике чаще всего приходится иметь дело с такими трубопроводами, движение жидкости в которых обусловлено работой насоса.

Пусть простой трубопровод постоянного сечения расположен в пространстве (рис. 1), имеет общую длину l, диаметр d и содержит ряд местных сопротивлений. В начальном сечении 1-1 имеем геометрическую высоту z ₁ и давление p ₁, а в конечном сечении 2-2 – соответственно z ₂ и p ₂.

Скорость потока в этих сечениях вследствие постоянства диаметра d трубопровода одинакова и равна v.

Запишем уравнение Бернулли для сечений 1-1 и 2-2.

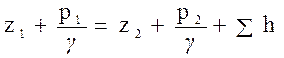Сокращая скоростные напоры, так как v ₁ = v ₂ = v, α₁ = α₂, получаем

или

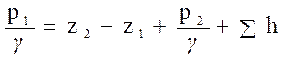Пьезометрическую высоту, стоящую в левой части уравнения, называют потребным напором Н _потр

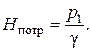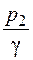Как видно из формулы, этот напор складывается из разности геометрических высот ∆ z = z ₂ – z ₁, на которую поднимается жидкость по трубопроводу, пьезометрической высоты в конце трубопровода и гидравлической потери напора в трубопроводе ∑ h.

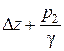Сумма слагаемых есть гидростатический напор и его можно представить как некоторую эквивалентную геометрическую высоту H _ст подъема жидкости – статический напор

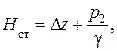а последнее слагаемое ∑ h – как степенную функцию расхода h = KQ^m. Тогда

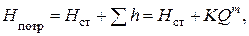
(3)

где величина K, называемая сопротивлением трубопровода, и показатель m имеют разные значения в зависимости от режима движения.

Для ламинарного движения, заменяя местные потери напора эквивалентными линейными потерями, получаем по формулам из теории ламинарного движения

Дата добавления: 2015-06-27