
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оптимальный раскрой
|
|
|
|
Большинство материалов, используемых в промышленности, поступает на производство в виде стандартных форм. Непосредственное использование таких материалов, как правило, невозможно. Предварительно их разделяют на заготовки необходимых размеров. Это можно сделать, используя различные способы раскроя материала. Задача оптимального раскроя состоит в том, чтобы выбрать один или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов. Задачи такого типа возникают в металлургии и машиностроении, лесной и лесообрабатывающей, легкой промышленности.
Различаются два этапа решения задачи оптимального раскроя. На первом этапе определяются рациональные способы раскроя материла. Способ раскроя называется рациональным, если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида. На втором этапе решается задача линейного программирования для определения интенсивности использования рациональных способов раскроя.
Определение рациональных способов раскроя материла.
В задачах оптимального раскроя рассматриваются так называемые рациональные (парето-оптимальные) способы раскроя. Предположим, что из единицы материала можно изготовить заготовки нескольких видов. Способ раскроя единицы материала называется рациональным (парето-оптимальным) если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.
Пусть
k — индекс вида заготовки, 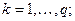
i — индекс способа раскроя единицы материала, 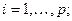
aik — количество (целое число) заготовок вида k, полученных при раскрое единицы материала способом i.
Приведенной выше определение рационального способа раскроя может быть формализовано следующим образом.
Способ v раскроя называется рациональным (парето-оптимальным), если для любого другого способа раскроя i из соотношений  ,
, 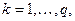 следуют соотношения
следуют соотношения 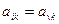 ,
, 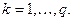
Пример
Требуется определить все рациональные способы раскроя деревянного бруса длиной 600 см на заготовки длиной 500, 300 и 200 см.
| Способы раскроя | 500 см | 300 см | 200 см | Отходы |
| - | ||||
| - | - | |||
| - | - | |||
| - | ||||
Определение интенсивности использования рациональных способов раскроя.
Обозначения:
j — индекс материала, 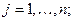
k — индекс вида заготовки, 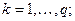
i — индекс способа раскроя единицы материала, 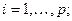
ajik — количество (целое число) заготовок вида k, полученных при раскрое единицы j - го материала способом i;
bk — число заготовок вида k в комплекте, поставляемом заказчику;
dj — количество материала j -го вида;
xji — количество единиц j -го материала, раскраиваемых по i -му способу (интенсивность использования способа раскроя);
сji — величина отхода, полученного при раскрое единицы j -го материала по i -му способу;
y — число комплектов заготовок различного типа, поставляемом заказчику.
Модель A раскроя с минимальным расходом материалов.
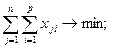 (1)
(1)
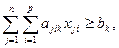
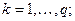 (2)
(2)
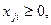
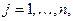
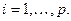 (3)
(3)
(1) — целевая функция — минимум количества используемых материалов;
(2) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(3) — условия неотрицательности переменных.
Модель позволяет обеспечить требуемое количество заготовок каждого типа с минимальными затратами материала. Специфическими для данной области приложения модели линейного программирования являются ограничения вида (2).
Пример
| Переменная | Способ раскроя | 500 см | 300 см | 200 см | Отходы |
| x1 | |||||
| x2 | |||||
| x3 | |||||
| x4 | |||||
| x5 | |||||
| x6 |
x1-4 — 1-й вид материала длиной 600 см
x5-6 — 2-1 вид материала длиной 500 см
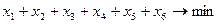
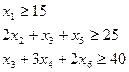
Получаем, что
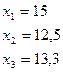
Округление всегда делается в большую сторону.
Модель Б раскроя с минимальными отходами
 (4)
(4)
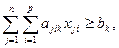
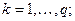 (5)
(5)
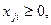
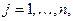
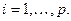 (6)
(6)
(4) — целевая функция — минимум отходов при раскрое материалов;
(5) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(6) — условия неотрицательности переменных.
Модель позволяет обеспечить требуемое количество заготовок каждого типа с минимальными отходами материала.
Модель В раскроя с учетом комплектации
 (7)
(7)
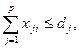
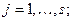 (8)
(8)
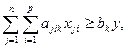
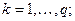 (9)
(9)
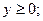
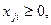
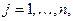
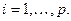 (10)
(10)
(7) — целевая функция — максимум комплектов, включающих заготовки различных видов;
(8) — огранич6ения по количеству материалов;
(9) — система ограничений, определяющих количество заготовок, необходимое для формирования комплектов;
(10) – условия неотрицательности переменных.
При ограничениях на объем используемого материала определяется максимальное число комплектов заготовок. Специфическими для данной области приложения модели линейного программирования являются ограничения вида (9).
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 1584; Нарушение авторских прав?; Мы поможем в написании вашей работы!