Пример 11

Пример 10.

Установить выводимость формулы А~В, Ø В├ Ø А

а) Построение формального вывода.

1. А~В	1. посылка
2. Ø В	2. посылка
3. (А~В)É(АÉВ)	3. АС12
4. АÉВ	4. МР(F1,F3)
5. (АÉВ)É((АÉØВ)ÉØА)	5. АС9
6. (АÉØВ)ÉØА	6. МР(F4,F5)
7. ØВÉ(АÉØВ)	7.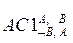
8. АÉØВ	8. МР(F2,F7)
9. ØА	9. МР(F6,F8)

б) Доказательство существования формального вывода.

1. А~В, ØВ, А├ ØВ	1. МТ1а
2. А~В, ØВ, А├ А	2. МТ1а
3. А~В, ØВ, А├ А~В	3. МТ1а
4. А~В├ АÉВ	4. УЭ1
5. А, АÉВ├В	5. МР
6. А~В, ØВ, А├ АÉВ	6. МТ1б(3, 4)
7. А~В, ØВ, А├В	7. МТ1б(2, 5, 6)
8. А~В, ØВ├Ø А	8.ВО(1, 7)

в) Замена вопроса о выводимости вопросом о следовании в алгебре высказываний.

А~В, ØВ╞Ø А

Установим верность данного следования методом от противного. Предполагаем, что следование не верно, т.е. при истинных посылках заключение является ложным. Получается следующая система уравнений:

противоречие.

Значит, следование является верным. Таким образом, установили данную выводимость.

Установить доказуемость формулы ├ АÙ(АÚВ)~А

а) Построение формального доказательства.

1. (АÙ(АÚВ)É А)É((АÉ АÙ(АÚВ))É(АÙ(АÚВ)~А))	1.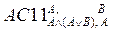
2. АÙ(АÚВ)É А	2.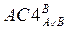
3. (АÉ АÙ(АÚВ))É(АÙ(АÚВ)~А)	3. МР(F1,F2)
4. (АÉАÚВ)É((АÉ(АÚВÉАÙ(АÚВ)))É(АÉАÙ(АÚВ)))	4.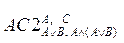
5. АÉАÚВ	5. АС6
6. (АÉ(АÚВÉАÙ(АÚВ)))É(АÉАÙ(АÚВ))	6. МР(F4,F5)
7. АÉ(АÚВÉАÙ(АÚВ))	7.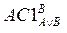
8. АÉАÙ(АÚВ)	8. МР(F6,F7)
9. АÙ(АÚВ)~А	9. МР(F3,F6)

б) Установление существования формального доказательства.

1. А├А	1. МТ1а
2. А├АÚВ	2. ВД1
3. А, АÚВ├АÙ(АÚВ)	3. ВК
4. А├АÙ(АÚВ)	4.МТ1б(1, 2, 3)
5. ├АÉАÙ(АÚВ)	5. ТД(4)
6. АÙ(АÚВ)├А	6. УК1
7. ├АÙ(АÚВ)ÉА	7. ТД(6)
8. АÉАÙ(АÚВ), АÙ(АÚВ)ÉА├ АÙ(АÚВ)~А	8.ВЭ
9. ├АÙ(АÚВ)~А	9. МТ1б(5, 6, 7)

в) Замена вопроса о доказуемости вопросом об общезначимости в алгебре высказываний.

╞ АÙ(АÚВ)~А

Докажем общезначимость формулы методом равносильных преобразований.

Будем также учитывать, что АÚИºИ, обозначим данное соотношение (*).

АÙ(АÚВ)~А 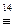(АÙ(АÚВ)ÉА)Ù(АÉАÙ(АÚВ)) 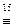(Ø(АÙ(АÚВ))ÚА)Ù(ØАÚАÙ(АÚВ)) 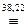(ØАÚАÚÚØ(АÚВ))Ù(ØАÚАÙ(АÚВ)) 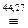(ИÚØ(АÚВ))Ù(ØАÚАÙАÚАÙВ) 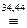(ИÚØ(АÚВ))Ù(ИÚАÙВ) 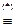ИÙ ÙИ И.

Контрольные вопросы

1. Алфавит, формулы, система аксиомных схем, правило вывода теории L.

2. Формальное доказательство и формальный вывод.

3. Свойства отношения выводимости.

4. Метод доказательства теоремы дедукции.

5. Непротиворечивость теории L.

6. Правила введения и удаления логических операторов.

7. Полнота теории L.

8. Адекватность теории L алгебре высказываний.

9. Разрешимость теории L.

10. Независимость аксиом теории L.

Задания для самостоятельного выполнения

1. Укажите выводом какой формулы и из каких посылок является следующая последовательность формул:

а) АÉС, (АÉС)É((ВÉС)É(АÚВÉС)), (ВÉС)É(АÚВÉС), ВÉС, АÚВÉС, АÚВ, С.

б) (АÉВ)É((АÉØВ)ÉØА), АÉВ, (АÉØВ)ÉØА, АÉØВ,ØА.

в) (АÉВ)É((ВÉА)É(А~В)), АÉВ, (ВÉА)É(А~В), ВÉА, А~В.

г) (АÉВ)É(ØВÉØА), АÉВ, ØВÉØА, ØВ, ØА.

2. Постройте данный вывод и результирующий вывод, применяя метод доказательства теоремы дедукции:

а) A, B├ AÙB

б) PÙQ├ P

в) P├ PÚ Q

г) AÉB, BÉA├ A~B

д) P~Q├ PÉQ

е) АÉВ, АÉØВ├ ØА

3. Постройте данный вывод и результирующий вывод, применяя метод доказательства теоремы дедукции:

а) CÉA, CÉB, C├ AÙB

б) AÙB, AÉ(BÉC)├ C

в) AÉB, BÉC├ AÉC

г) (AÉC)ÉC, AÉB, BÉC├ C

д) AÉB, ØB├ ØA

е) AÉB, CÉE, ØBÙØE├ ØAÙØC

ж) А ~В, В ÉС├ АÉС

з) АÉС, ØВÉА├ ØВÉС

и) ВÉØА, А├ ØВ

к) AÉB, AÉØB├ ØAÚB

л) A~B, ØB├ ØA

м) A~B, B~C├ A~C

н) A├ BÉB

о) ØAÉB, CÙØB├ A

4. Постройте доказательства:

а) АÉAÙA

б) AÙA~А

в) AÚ (A~А)

г) AÙВÉAÚВ

д) Ø(BÙØB)

5. Дано доказательство:

1. (А É (ВÉA)) É ((A É ((ВÉA) É A))É (А É A))	1.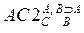
2. А É (ВÉA)	2. АС1
3. (A É ((ВÉA) É A)) É (А É A)	3. МР(F2,F1)
4. A É ((ВÉA) É A)	4.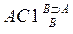
5. А É A	5. МР(F4,F3)
6. ├ AÉ А	6. ОФД (1-5) – определение формального доказательства

Дополните его до доказательства формулы A~А.

6. Установите существование доказательств следующих формул:

а) ├ (АÉВ)Ù(ВÉС)É(АÉС)

б) ├ (АÉ(ВÉС))É(АÙВÉС)

в) ├ (АÙВÉС)É(АÉ(ВÉС))

г) ├ АÉ(ВÉАÙВ)

д) ├ (АÉВ)É(АÉ(АÉВ))

7. Установите следующие выводимости:

а) A,ØB├ AÉØB

б) ØAÙØB, A├ B

в) Ø(AÚB),B├ AÚB

г) AÉBÚC, DÉA, DÙEÉØB├ DÙEÉC

д) AÙØB, AÉB├ С

е) B, AÙØC, AÉ(BÉC)├ A~B

ж) A~B,ØB├ ØA

з) A~B, B~C├ AÉC

и) AÙØB, AÉB├ C

к) AÚBÚC, DÙØB, DÉØC├ A

л) AÉB, AÙC├ BÙC

м) AÉBÚC, AÙØB├ C

н) AÙBÉC,ØC├ ØAÚØB

о) AÚBÉC,ØC├ ØAÙØB

п) ØAÙØB,ØBÉA├ C

р) B, AÉØB├ Ø(ØBÚA)

с) ØAÉB, CÙØB├ A

т) AÉB, CÉD,ØBÙØD├ ØAÙØC

у) ØAÉB,ØCÉD,ØBÚØD├ AÚC

ф) AÙBÉC, AÙØC├ ØB

х) AÉB, CÉD, AÚC,ØBÚØD├ BÉA.

8. Установите следующие доказуемости:

а) AÙA~А

б) AÚАÙB~А

в) АÉ(ВÉС)~ АÙВÉС

г) АÉВ~ØВÉØА

д) Ø(АÙВ)~ØАÚØВ

е) (А~В)~(В~А)

ж) AÙ(ВÙС)~(AÙВ)ÙС

з) AÚ(ВÚС)~(AÚВ)ÚС

и) AÚØАÙВ~ AÚВ

к) АÙВ~Ø(ØАÚØВ)

л) АÚВ~Ø(ØАÙØВ)

м) Ø(АÉВ)~АÙØВ

н) АÉВ~ØАÚВ

о) AÚ (ВÙС)~(AÚВ)Ù(АÚС)

п) AÙ(ВÚС)~(AÙВ)Ú(АÙС)

Литература

1. Латотин Л.А., Макаренков Ю.А., Николаева В.В., Столяр А.А. Математическая логика. – Минск: «Вышейшая школа». 1991.

2. Лихтарников Л.М., Сукачева Т.Г. Математическая логика: курс лекций, задачник-практикум и решения. – СПб.:[б.и.], 1999.

3. Игошин В.И. Задачник-практикум по математической логике. – М.: Просвещение, 1986.

Дата добавления: 2015-06-27