Основные процедуры эвристического поиска

Процедура expo(«расширить») будет возвращать 3 типа результатов: 1, 0, -1 (никогда).

expo(Путь, Дерево, Предел, Дерево1, Да, Решение).

Путь — путь от стартовой вершины до корня текущего дерево;

Дерево — текущее расширенное дерево;

Дерево1 — его расширение;

Предел — предельное значение f-оценки дерева, при котором его расширение еще возможно.

Если f-оценка текущего дерева > предела, то эвристический поиск переключается на другое дерево и делает его текущим.

Правила процедуры expo:

1 — расширяемый лист целевая вершина;

2 — расширили лист Х до дерева с корнем Х;

3 — тупиковый лист;

4 — расширяем текущее дерево, т.к. его оценка ≤ Limit;

5 — все поддеревья тупиковые, Yes = -1;

6 — оценка F текущего дерева > Limit, рост дерева прекращается, т.е. D1 = D (расширенное = исходное) и Yes = 0.

Список поддеревьев DD будет упорядочен по возрастанию F-оценок, т.е. 1-е поддерево списка имеет минимальную F-оценку. Предикат optf будет возвращать минимальную оценку хвоста списка поддеревьев:

optf(DD,OF).

Значение Limit1 выбирается как минимальное из Limit и OF:

Limit1=min{Limit,OF}.

Таким образом, пока возможно, мы расширяем, не выходя их текущего дерева. Расширенное дерево вставляется согласно его F-оценке процедурой prolong.

Рассмотрим правила процедуры prolong.

1. Для расширения была выбрана целевая вершина, expo вернула 1 и prolong была вызвана с 1;

2. expo вернула 0, расширенное дерево D1 вставлено в DD согласно F-оценке, затем expo вызывается с новым списком поддеревьев DD1;

3. expo вернула — 1, т.е. D-тупиковое и удаляется из списка, DD1 = DD.

1.5.3. Пространство состояний игры в «8»

Пространство состояний игры в «8» относительно невелико: 9!=362880 различных конфигураций. Оно делится на 2 непересекающихся подпространства в 181440 состояний. Любые 2 конфигурации, взятые из различных подпространств, являются непереводимыми.

Итак, имеется 9 фишек: 0 (пусто), 1..8. Каждая фишка имеет x, y координату. На рис. 8 изображена заключительная конфигурация или целевое состояние для игры в «8». C(X,Y) — координаты фишек. Конфигурация (состояние) — список координат 9 фишек в последовательности 0..8.

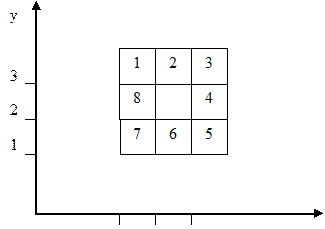
Рисунок 9. Целевое состояние для игры в «8» с осями координат

Целевое состояние:

[c(2,2), c(1,3), c(2,3), c(3,3), c(3,2), c(3,1), c(2,1), c (1,1), c(1,2)].

Разрешенные ходы: фишка 0 меняется местами с соседней фишкой. Соседняя фишка — фишка, находящаяся на расстоянии равном 1.

Общее расстояние D=DX+DY, где DX и DY — расстояния по горизонтали и вертикали.

Опишем предикат dist(F1,F2,D), вычисляющий расстояние по координатам двух фишек.

dist(c(X,Y),c(X1,Y1),D):-

dist1(X,X1,DX),

dist1(Y,Y1,DY),

D=DX+DY.

dist1(Z,Z1,DZ):-

DZ=abs(Z-Z1).

Стоимость каждого хода положим равной 1. При обмене фишки «0» с какой-то фишкой «j» (при условии, что они находятся на расстоянии 1) происходит обмен координатами фишек «0» и «j» (рис. 10).

Рисунок 10. Обмен координатами между фишками F₀ и F_j

Рассмотрим процедуру go(Pos1,Pos2,1), переводящее состояние Pos1 в Pos2 со стоимостью хода, равной 1.

go([F0|T],[Fsh|T1],1):-

change(F0,Fsh,T,T1).

F0 — координаты фишки «0» до обмена, Fsh — координаты фишки «0» после обмена, т.е. координаты той фишки, с которой «0» обменялась местами. В T1 для фишки, обменявшейся с «0» будут записаны координаты «0», т.е. F0.

Рекурсивную процедуру обмена change разделим на 2 правила: фишка «0» меняется местами с «1» и фишка «0» меняется местами не с «1».

% «0» меняется с «1»

change(H,F,[F|T],[H|T]):-

dist(H,F,1).

% "0" меняется не с "1"

change(H,F,[F1|T],[F1|T1]):-

change(H,F,T,T1).

Таким образом, мы полностью определили пространство состояний и разрешенные ходы.

Зададим 3 стартовые позиции (рис.11):

(4 хода) (5 ходов) (18 ходов)

Рисунок 11. Три стартовые позиции игры в «8»

Дата добавления: 2015-06-27