Экспертные системы. Программная реализация эвристического поиска на И-ИЛИ графе

Задача о мостах

Программная реализация эвристического поиска на И-ИЛИ графе

Теперь нам придется различать деревья поиска и деревья решения. Это связано с тем, что в дереве поиска для ИЛИ-вершины нужно помнить всех ее преемников, а в дереве решения у ИЛИ-вершины будет ровно один преемник. Соответственно, будем различать 6 типов деревьев:

лист, «И»-дерево, «ИЛИ»-дерево для деревьев поиска и

лист, «И» — дерево, «ИЛИ»-дерево для деревьев решения.

Кроме того, для дерева будем явно хранить следующую информацию:

· Корень (тип корня определен типом дерева).

· f-оценку корня.

· Стоимость дуги из родительской вершины в корень.

· Список поддеревьев.

Список поддеревьев будет упорядочен таким образом, что все решающие деревья будут находится в конце списка, а деревья поиска (деревья — кандидаты в решение) будут упорядочены по возрастанию f-оценок.

Припишем веса дугам модельного графа в задаче о мостах (рис. 16).

Зададим исходную информацию фактами базы данных. Информация о расстоянии будет представлена фактами следующего типа:

edge(a,b,2). edge(a,c,3). edge(b,d,2).

edge(b,e,3). edge(c,e,1). edge(d,f,1).

edge(e,f,4). edge(e,g,2). edge(c,g,2).

edge(f,h,3). edge(f,i,2). edge(g,j,1).

edge(i,j,5). edge(h,z,3). edge(i,z,2).

edge(j,k,3). edge(k,z,3).

Информация о ключевых пунктах будет представлена фактами типа:

kpp(a,z,f). kpp(a,z,g).

Опишем алгоритм поиска пути, основанного на эвристическом поиске на И-ИЛИ графе.

Для нахождения пути между X и Z необходимо:

1. Если между X и Z есть ключевые пункты Y₁, Y₂,..., то найти один из путей «из X в Z через Y_i»;

2. Если ключевых пунктов нет, то найти Y₁, Y₂,... — соседние с X вершины и найти один из путей «из Y_i в Z».

Таким образом, мы имеем два типа задач:

X-Z % найти путь из X в Z;

X-Z через Y % найти путь из X в Z через Y.

Согласно нашему алгоритму задача X-Z всегда будет ИЛИ-вершиной; задача X-Z через Y всегда будет И-вершиной. Это не всегда так. Могут быть проблемные ситуации, где каждый тип задачи может становиться и «И», и «ИЛИ»-вершиной.

В нашем примере первый тип задач порождает ИЛИ-деревья, второй тип — И-деревья.

Рассмотрим, как происходит формирование «И» и «ИЛИ»-вершин и приписывание стоимостей дугам И-ИЛИ графа.

Если между X и Z имеются ключевые пункты (рис. 30), то дугам приписывается стоимость 0, так как размер исходной задачи не изменяется, а произошло перечисление различных вариантов решения задачи.

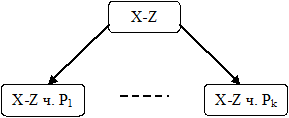
Рисунок 30. Сведение задачи типа «найти путь из X в Z» к задачам типа «найти путь из X в Z через ключевой пункт P_i»

Если ключевых пунктов нет, то находим для X все соседние вершины Y₁, …,Y_k (рис. 31).

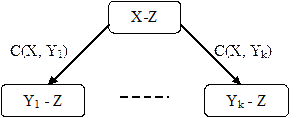
Рисунок 31. Сведение задачи типа «найти путь из X в Z» к задачам типа «найти путь из Y_i в Z» где Y_i — соседки вершины X

Так как вершина Y_i является соседней для X, то считаем, что задача «X-Y_i» уже решена и не включаем ее в дерево. Поскольку первоначальная задача «X-Z» свели к задаче «Y_i-Z» стоит c(X,Y_i).

Задачу «X-Z через Y» разбиваем на подзадачи «X-Y» и «Y-Z», стоимости дуг равны 0 (рис. 32):

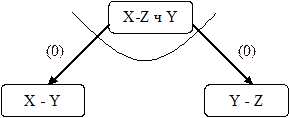
Рисунок 32. Задача типа «найти путь из X в Z через Y» является
«И»-вершиной со стоимостями дуг равными нулю

Теперь выясним, какие вершины для И-ИЛИ графа являются терминальными. Для графа пространства состояний, соответствующего карте, вершина Z была бы целевой. Для И-ИЛИ графа целевыми являются тривиальные задачи следующего типа (рис. 33).

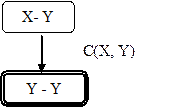
Рисунок 33. Сведение задачи типа «найти путь из X в Y по ребру» к тривиальной задаче типа «найти путь из Y в Y» со стоимостью дуги равной стоимости ребра

Итак, prob(X,X) — тривиальные вершины. Стоимость их решения — 0.

Нам нужно решить задачу «X-Y», обнаруживаем, что Y — соседка X. Свели задачу «X-Y» к задаче «Y-Y». Задача «Y-Y» является тривиальной, стоимость ее решения — 0.

Задача «X-Z через Y» порождает подзадачи X-Y и Y-Z, поэтому она является «И»–вершиной со стоимостями дуг равными 0 (рис. 32).

Типы задач.

punct = symbol % город на карте, а не вершина графа

u = prob(punct,punct); % 1-й тип задач

prob(punct,punct,punct) % 2-й тип задач

В модуле orand.pro содержится непосредственно эвристический поиск на И-ИЛИ-графе. В модуле orand.dat — эвристики и правила для задачи о мостах.

/* Листинг модуля orand.dat */

predicates

edge(punct,punct,int)

kpp(punct,punct,punct)

end(u)

tor(u,lcost)

tand(u,lcost)

pp(punct,punct,cost)

ed(punct,punct,cost)

a(u,int)

classes

h(_,0)

edge(a,b,z)...

end(prob(X,X)):!.

kpp(a,z,f).

kpp(a,z,g).

%"И" – вершина со списком соседок

tand(prob1(A,Z,Y),[co(prob(A,Y),0),co(prob(Y,Z),0)]):-

kpp(A,Z,Y).

%"ИЛИ" – вершина со списком соседок

tor(prob(A,Z),Lprob):-

findall(Problem,pp(A,Z,Problem),Lprob),

Lprob=[H|T],!. %если есть ключевые пункты, переход

% вниз запрещен

tor(prob(A,Z),Lprob):-

findall(Problem,ed(A,Z,Problem),Lprob).

Pp(A,Z,Problem):-

kpp(A,Z,Y),

Problem=co(prob1(A,Z,Y),0).

ed(A,Z,Problem):-

edge(A,Y,P),

Problem=co(prob(Y,Z),P).

/* Листинг модуля orand.pro */

/* ПОСТРОЕНИЕ ЕДИНСТВЕННОГО ДЕРЕВА РЕШЕНИЯ */

/* НА "И-ИЛИ" ГРАФЕ ЭВРИСТИЧЕСКИМ ПОИСКОМ. */

/* Построенное дерево решения является min, если */

/* для каждой вершины u графа эвристика h(u) */

/* h(u)<=h^*(u), где h^*(u)-стоимость min решающего */

/* дерева с корнем в вершине u. */

/*****************************************************/

constants fmax=9999

/*****************************************************/

domains

punct=symbol %город на карте

int=integer

% 2 типа задач - вершин "И-ИЛИ" графа

u=prob(punct,punct); %найти путь от A до Z

prob1(punct,punct,punct) %найти путь от A до Z через X

cost=co(u,int) %вершина со стоимостью входящей дуги

lcost=cost* %список соседок

% пара (f(u),c(u)), где f(u)=c(u)+hback(u)

est = e(int,int)

% c(u) - стоимость дуги, входящей в u

% hback(u) - "возвращенная" эвристика u,

% которая оценивает стоимость min решающего дерева

% с корнем в вершине u, равную h^*(u)

% шесть типов деревьев

tree = %деревья поиска

l(u,est); %лист, если u - целевая вершина

to(u,est,treelist);%"ИЛИ"-дерево, если u - "ИЛИ"-%вершина

%"ИЛИ"-дерево ПОИСКА

%содержит ВСЕ "ИЛИ"-поддеревья

ta(u,est,treelist);%"И"-дерево, если u - "И"-вершина

%деревья решения

sl(u,int); %РЕШлист, если u - целевая вершина

sto(u,int,tree); %"ИЛИ"-РЕШдерево, если u - "ИЛИ"-%вершина

%содержит одно "ИЛИ"-дерево

sta(u,int,treelist)%И"-РЕШдерево, если u - "И"-вершина

treelist = tree* %список поддеревьев

predicates

show(tree)

show4(tree)

show1(tree,int)

show2(treelist,int)

tab(int)

solve(u,tree)

expo(tree,int,tree,int)

f(tree,int)

expol(u,int,tree)

expolist_a(treelist,int,treelist,int)

expolist_or(treelist,int,treelist,int)

prolong(int,u,int,treelist,int,tree,int)

case_a(treelist,tree,treelist,int,int)

case_or(treelist,tree,treelist,int,int)

adda(treelist,tree,int,treelist,int)

addor(treelist,tree,int,treelist,int)

estor_h(treelist,int)

esta_h(treelist,int)

yesall(treelist)

yes(tree)

make_tlist(lcost,treelist)

into(tree,treelist,treelist)

min(int,int,int)

include "orand.dat"

goal

clearwindow,

solve(prob(a,z),D), write(D),nl,show(D),nl,

nl,write("stoimost = "), show4(D).

clauses

% цель верхнего уровня

solve(A,SD):-

h(A,H),

expo(l(A,e(H,0)),fmax,SD,Yes),

Yes=1,!.

/***** процедура расширить *************************/

% (1) - выход за ограничение,

expo(D,Limit,D,0):-

f(D,F), % нашли F-оценку D

F > Limit,!.

% в правилах (2-5) для expo случай F <= Limit.

% (2) - нашли целевую вершину.

expo(l(X,e(F,C)),_,sl(X,F),1):-

end(X),!.

% (3,4) - порождение преемников листа.

expo(l(X,e(F,C)),Limit,D1,Yes):-

expol(X,C,D),!, % расширить_лист X

expo(D,Limit,D1,Yes).

% (4) - тупиковый лист

expo(l(X,e(F,С)),Limit,_,-1):-!.

% (5) - расширить дерево поиска типа "и"

expo(ta(X,e(F,C),DD),Limit,Dr1,Yes):-

Limit1=Limit - C,

expolist_a(DD,Limit1,DD1,Yes1),!, %расширить_и_список %DD

prolong(Yes1,X,C,DD1,Limit,Dr1,Yes). % продолжить

% (6) - расширить дерево поиска типа "или"

expo(to(X,e(F,C),DD),Limit,Dr1,Yes):-

Limit1=Limit - C,

expolist_or(DD,Limit1,DD1,Yes1),!,%расширить_или_список DD

prolong(Yes1,X,C,DD1,Limit,Dr1,Yes). % продолжить

/******************************************************/

/********** процедура расширить_и_список *********/

% расширяет деревья из заданного "и"-списка DD

% с учет ограничения Limit

expolist_a(DD,Limit,DD1,Yes):-

case_a(DD,D,TDD,Limit,Limit1), % выбираем D из списка DD

expo(D,Limit1,Dr1,Yes1), % расширяем D до Dr1

adda(TDD,Dr1,Yes1,DD1,Yes). % соединяем Dr1

% с оставшимся "и"-списком TDD

% расширяет заданный "или"-список DD

% с учет ограничения Limit

expolist_or(DD,Limit,DD1,Yes):-

case_or(DD,D,TDD,Limit,Limit1), % выбираем D из
% списка TDD

expo(D,Limit1,Dr1,Yes1), % расширяем D до Dr1

addor(TDD,Dr1,Yes1,DD1,Yes). % соединяем Dr1

% с оставшимся "или"-%списком TDD

/******************************************************/

/********** процедура продолжить ******************/

% продолжить решает, что делать после расширения списка %деревьев

% (1) - нашли решающее "ИЛИ" - дерево

prolong(1,X,C,DD,_,sto(X,F,D),1):-

tor(X,_),!, % X - "или"-вершина

estor_h(DD,H), % H = hback(X) = min{ F(D): D из DD }

DD=[D],

F=C+H, % f-оценка вершины X

!.

% (2) - нашли решающее "И" - дерево

prolong(1,X,C,DD,_,sta(X,F,DD),1):-

tand(X,_),!, % X - "и"-вершина

esta_h(DD,H), % H = hback(X) = сумма{ F(D): D из DD }

F=C+H, % f-оценка вершины X

!.

% (3) - расширить нельзя

prolong(-1,_,_,_,_,_,-1):-!.

% (4) - расширили до "ИЛИ" - дерева поиска

prolong(0,X,C,DD,Limit,Dr1,Yes):-

tor(X,_),!, % X - "или"-вершина

estor_h(DD,H), % H - стоимость min поддерева из DD

F=C+H,!, % f-оценка вершины X

expo(to(X,e(F,C),DD),Limit,Dr1,Yes).

% (5) - расширили до "И" - дерева поиска

prolong(0,X,C,DD,Limit,Dr1,Yes):-

tand(X,_),!, % X - "и"-вершина

esta_h(DD,H), % H - суммарная стоимость %поддеревьев из DD

F=C+H,!, % f-оценка вершины X

expo(ta(X,e(F,C),DD),Limit,Dr1,Yes).

/******************************************************/

/*** процедуры добавить_и и добавить_или **********/

% добавить_и соединяет дерево с "и"-списком

% (1) - все деревья "и"-списка - решающие

adda(DD,D,1,[D|DD],1):-

yesall(DD),!.

% into(D,DD,DD1).

% (2) - нет решения "и"-списка, так как дерево - тупиковое

adda(_,_,-1,_,-1):-!.

% (3) - расширенное дерево, может быть, содержит
% решение, но неизвестно, являются ли решающими
% остальные поддеревья

adda(DD,D,Yes_No,DD1,0):-

Yes_No<>-1,

into(D,DD,DD1),!.

% добавить_или соединяет дерево с "или"-списком

% (1) - решающее расширенное дерево

addor(_,D,1,[D],1):-!.

% (2) - в расширенном дереве нет решения

addor(DD,D,0,DD1,0):-

into(D,DD,DD1),!.

% (3) - дерево тупиковое, и в "или"-списке

% больше нет кандидатов в решение

addor([],_,-1,_,-1):-!.

% (4) - дерево тупиковое, но в "или"-списке

% есть еще кандидаты в решение

addor(DD,_,-1,DD,0):-!.

/********* процедура расширить_лист ***************/

% формирует дерево поиска из X и ее премников

% (1) X - "или"-вершина

expol(X,C,to(X,e(F,C),DD)):-

tor(X,L),

make_tlist(L,DD), % DD - список листов

estor_h(DD,H), % H - стоимость min листа из DD

F=C + H. % f-оценка вершины X

% (2) X - "и"-вершина

expol(X,C,ta(X,e(F,C),DD)):-

tand(X,L),

make_tlist(L,DD), % DD - список листов

esta_h(DD,H), % H - суммарная стоимость листов из DD

F=C + H. % f-оценка вершины X

/********** процедура построить_список *************/

% из списка преемников Y вершины X построить список
% листов DD

make_tlist([],[]).

make_tlist([co(Y,C)|TY],DD):-

h(Y,H), % H = hback(Y) = h(Y), т.к. Y - лист

F=C+H, % f-оценка листа Y

make_tlist(TY,TDD),

into(l(Y,e(F,C)),TDD,DD).

/******************************************************/

/* процедуры оценка_"или"-списка и оценка_"и"-списка */

% "возвращенная" h-оценка "или"-списка

% (1) - первое дерево "или"-списка - минимальное

estor_h([D|_],F):-

f(D,F),!. % нашли F-оценку D

% (2) - нулевая оценка пустого "и"-списка

esta_h([],0):-!.

% (3) - оценка непустого "и"-списка

esta_h([D1|DD],F):-

f(D1,F1),

esta_h(DD,FF),

F = F1+FF.

/********** процедура f_оценка дерева *************/

% (1) - лист поиска

f(l(_,e(F,_)),F):-!.

% (2) - дерево поиска типа "и"

f(ta(_,e(F,_),_), F):-!.

% (3) - дерево поиска типа "или"

f(to(_,e(F,_),_), F):-!.

% (4) - решлист

f(sl(_,F),F):-!.

% (5) - решдерево типа "и"

f(sta(_,F,_), F):-!.

% (6) - решдерево типа "или"

f(sto(_,F,_), F):-!.

/********* процедуры на решающие деревья **********/

% проверка, все ли деревья "и"-списка являются решающими

yesall([]).

yesall([D|DD]):-

yes(D),

yesall(DD).

% проверка, является ли дерево решающим

yes(sl(_,_)):-!.

yes(sto(_,_,_)):-!.

yes(sta(_,_,_)):-!.

/********* процедура вставки **********************/

% вставка дерева D в список DD

% с сохранением упорядоченности f-оценок

% решающие деревья расположены в конце списка

into(D,[],[D]):-!.

into(D,[D1|DD],[D,D1|DD]):-

yes(D1),!.

into(D,[D1|DD],[D1|DD1]):-

yes(D),

into(D,DD,DD1),!.

into(D,[D1|DD],[D,D1|DD]):-

f(D,F), f(D1,F1),

F<=F1,!.

into(D,[D1|DD],[D1|DD1]):-

into(D,DD,DD1).

/******** процедуры выбора case_a и case_or **********/

% выбираем min дерево D из списка DD

% Limit - ограничение для списка DD, Limit1 - ограничение для D

% (1) - одноэлементный список

case_a([D],D,[],Limit,Limit):-!.

% (2) - "и"-список

case_a([D|DD],D,DD,Limit,Limit1):-

esta_h(DD,H),!,

Limit1 = Limit - H.

% (1) - одноэлементный список

case_or([D],D,[],Limit,Limit):-!.

% (2) - "или"-список

case_or([D|DD],D,DD,Limit,Limit1):-

estor_h(DD,H),!,

min(Limit,H,Limit1).

min(X,Y,X):-

X<=Y,!.

min(X,Y,Y).

%печать дерева решения

show(sto(_,_,D)):-

show1(D,0).

show4(sto(_,D,_)):-

write(D).

show1(sl(prob(X,_),_),Tab):-

write(X),nl,!.

show1(sto(prob(X,_),_,D),Tab):-

write(X),

write("--->"),

Tab1=Tab+10,

show1(D,Tab1),!.

show1(sta(prob1(_,_,X),_,D),Tab):-

% write(X),

% write("--->"),

show2(D,Tab).

show2([D],Tab):-

show1(D,Tab),!.

show2([D|DD],Tab):-

show1(D,Tab),

tab(Tab),

show2(DD,Tab).

tab(0):-!.

tab(X):-

write(" "),

X1=X-1,

tab(X1).

Задание. Написать программу для решения задачи о мостах эвристическим поиском на «И-ИЛИ» графах. Распечатать путь. Найти стоимость решения.

Дата добавления: 2015-06-27