Точное вероятностное рассуждение

Общие проблемы

Вывод в условиях неопределенности

В жизни часто приходится оценивать гипотезы, для которых имеется неполная или недостаточная информация. Несмотря на неопределенность, удается принять разумное решение.

Классической иллюстрацией может служить медицинская диагностика. Всегда существует сомнение в наличии у пациентов конкретного заболевания, даже если его симптомы отчетливо выражены. Рассуждения, основанные на неопределенности, используются во всех системах медицинской диагностики.

Рассуждения в условиях неопределенности имеют место и при наличии одновременно нескольких конкурирующих гипотез и их постоянной переоценке по мере поступления новых данных. В конечном счете выделяется одна, наиболее достоверная гипотеза.

Системы распознавания речи также используют этот метод. Распознавание речи — очень сложная задача, поэтому в ней должны присутствовать конкурирующие гипотезы, например, о том, какое конкретное слово было употреблено в предложении.

Существует несколько важных проблем, когда вывод приходится делать в условиях неопределенности:

· определение степень достоверности данных;

· определить степень поддержки заключения конкретной посылкой;

· совместное использование двух и более правил, независимо поддерживающих одно и тоже заключение.

Прежде всего, изучим возможности использования теории вероятностей при выводе в условиях неопределенности.

Под точным вероятностным рассуждением подразумеваем рассуждение по правилам теории вероятностей. Условная вероятность — вероятность наступления события А, если В уже произошло.

Рассмотрим ситуацию, в которой используется простая импликация:

(если А, то В).

Предположим, что никакие другие правила или посылки не имеют отношения к данной ситуации. Разберемся, где возникает неопределенность. В системах вывода она бывает двух видов.

Во-первых, неопределенность возникает при попытке количественно оценить, насколько мы уверены, что посылка правила истинна. Например, если степень уверенности того, что А истинно, составляет 90%, то какое значение тогда примет В?

Другой вариант — неопределенность в самой импликации. Например, мы могли бы сказать, что в большинстве случаев если есть А, то есть также и В. Должно быть числовое выражение этого факта (скажем, мы на 95% уверены, что, имея А, мы имеем и В).

Как можно эти отношения выразить в терминах вероятности? Если бы была абсолютная гарантия, что предшествующее событие А истинно, то мы могли бы записать:

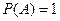
Когда полной определенности нет, установленное значение вероятности отражает эту информацию таким образом:

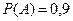
При неопределенности второго типа утверждение с вероятностью в 95%, что будет В, если есть А, записывается в форме условной вероятности:

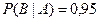
Эта формулировка достаточна ясна сама по себе, но она не дает никакой информации о том, может ли наступить В, если нет А. Для этого нужно знать еще одну вероятность:

Рассмотрим теперь типичную проблему. Импликация представляет собой выражение типа (если А, то В).

Проблему можно выразить следующим образом: мы на 90% уверены в том, что А истинно. Мы верим в это правило импликации на 95%. Какова вероятность, что В истинно?

Нам известно следующее:

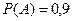
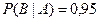
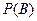— искомый результат.

Как вычислить 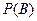? Можно применить правило композиции и с его помощью получить 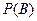на основе известных вероятностей:

Три величины мы знаем. Обратите внимание что:

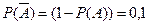
Поэтому после преобразования уже известных величин получается равенство:

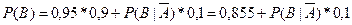
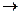
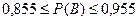
Если без А В никогда не наступает, то 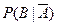=0

и, следовательно, Р(В) = 0,855.

Усложним импликацию. В этой ситуации для получения заключения могут присутствовать две посылки

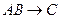(Если (А и В), то (С)).

Эксперт сообщил следующую информацию:

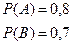
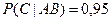
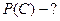
Если следовать формулировкам предыдущей задачи, то при использовании правила композиции получатся такие выражения для С:

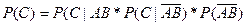
Теперь мы имеем две неизвестных величины вместо одной.

К сожалению, зная Р(А) и Р(В), невозможно получить Р(АВ).

На самом деле: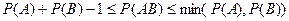

Для импликации типа если (А или В, или С), то (D) эта формула станет слишком сложной, и нам нужно будет знать столько вероятностей, сколько ни один эксперт не в состоянии сообщить. В этом заключается причина того, что в экспертных системах не используются точные вероятностные рассуждения.

Дата добавления: 2015-06-27