
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Синтез основного контура управления
|
|
|
|
Структурная схема контура положения представлена на рис. 7.5. Здесь  – ПФ замкнутого контура скорости, определяемая по методике, которая была использована для расчета ПФ контура напряжения:
– ПФ замкнутого контура скорости, определяемая по методике, которая была использована для расчета ПФ контура напряжения:


где  с – эквивалентная малая постоянная времени.
с – эквивалентная малая постоянная времени.

Рис. 7.5. Структурная схема контура положения
Синтез регулятора положения РП рекомендуется осуществлять с применением ЛЧХ. В основе этого подхода лежит процедура построения желаемой ЛАЧХ по исходным данным на проектирование. Однако сначала целесообразно построить ЛАЧХ нескорректированного разомкнутого контура положения, чтобы оценить частотный диапазон работы системы. Его ПФ равна
 ,
,
где  с-1.
с-1.
ЛАЧХ желательно строить на миллиметровой бумаге формата А4 с альбомным расположением листа. При этом целесообразно использовать следующий масштаб: по оси частот (абсцисс) – 1 декада = 5 см, по оси ординат – 1 см = 10  (децибел), как это показано на рис. 7.6.
(децибел), как это показано на рис. 7.6.
Наличие интегратора в ПФ 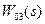 говорит о том, что низкочастотная часть ЛАЧХ исходного нескорректированного контура
говорит о том, что низкочастотная часть ЛАЧХ исходного нескорректированного контура  имеет наклон
имеет наклон  и проходит, через опорную точку
и проходит, через опорную точку  . Эту частоту необходимо откладывать по логарифмической оси lg ω, т.к. она равномерная. Таким образом, сначала вычисляется
. Эту частоту необходимо откладывать по логарифмической оси lg ω, т.к. она равномерная. Таким образом, сначала вычисляется  , откладывается на оси
, откладывается на оси  и затем через эту точку проводится прямая с отрицательным наклоном
и затем через эту точку проводится прямая с отрицательным наклоном  на одну декаду (это по существу гипотенуза треугольника со сторонами 2 см по оси ординат и 5 см по оси абсцисс). Данная
на одну декаду (это по существу гипотенуза треугольника со сторонами 2 см по оси ординат и 5 см по оси абсцисс). Данная 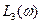 имеет излом в точке
имеет излом в точке  , равный
, равный  , т.е. суммарный наклон характеристики, начиная с этой частоты будет равен
, т.е. суммарный наклон характеристики, начиная с этой частоты будет равен  (рис. 7.6).
(рис. 7.6).
Для оценки точности воспроизведения входного воздействия  с заданными
с заданными  и
и  следует определить контрольную точку на ранее рассчитанной частоте
следует определить контрольную точку на ранее рассчитанной частоте 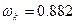 с-1 по соотношению
с-1 по соотношению

и отложить ее на рис. 7.6. Если исходная ЛАЧХ проходит ниже этой точки, то требуется коррекция по точности, если выше, то не требуется. В рассматриваемом примере 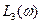 проходит ниже контрольной точки
проходит ниже контрольной точки  (рис. 7.6), поэтому коррекция по точности необходима.
(рис. 7.6), поэтому коррекция по точности необходима.
Далее можно перейти к построению желаемой ЛАЧХ  . При проектировании САУ методом ЛЧХ используют типовые характеристики
. При проектировании САУ методом ЛЧХ используют типовые характеристики  . Их низкочастотная часть обычно проходит через контрольную точку
. Их низкочастотная часть обычно проходит через контрольную точку  , как это показано на рис. 7.6, т.е. сначала проводится прямая под наклоном
, как это показано на рис. 7.6, т.е. сначала проводится прямая под наклоном  , а затем, начиная с частоты
, а затем, начиная с частоты  , под наклоном
, под наклоном  . Такая низкочастотная часть
. Такая низкочастотная часть  даст точность требуемую по техническому заданию.
даст точность требуемую по техническому заданию.
Среднечастотная часть  пересекает ось
пересекает ось  при
при  и проводится под наклоном
и проводится под наклоном  , причем длина этого участка берется в пределах
, причем длина этого участка берется в пределах  декады. Чем шире среднечастотная часть
декады. Чем шире среднечастотная часть  , тем будет меньше перерегулирование
, тем будет меньше перерегулирование  . Частота среза
. Частота среза  при которой
при которой 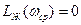 , подбирается исходя из заданной длительности переходного процесса
, подбирается исходя из заданной длительности переходного процесса  по приближенному соотношению
по приближенному соотношению
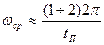 .
.
Следует заметить, что эта частота обычно многократно корректируется в процессе проверки желаемой САУ на выполнение требуемых показателей качества.
Пусть задано  Тогда в рассматриваемом примере получим
Тогда в рассматриваемом примере получим
 .
.
Возьмем из этого интервала  и проведем через точку
и проведем через точку  прямую под наклоном
прямую под наклоном  : влево до пересечения с прямой, имеющий наклон
: влево до пересечения с прямой, имеющий наклон  , вправо до частоты
, вправо до частоты 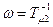 .
.
Высокочастотная часть начинается условно с частоты 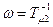 и проводится, исходя из простоты реализации получаемого корректирующего устройства. В рассматриваемом случае наклон
и проводится, исходя из простоты реализации получаемого корректирующего устройства. В рассматриваемом случае наклон  на этом участке следует взять таким же, как и в исходной ЛАЧХ
на этом участке следует взять таким же, как и в исходной ЛАЧХ 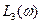 , т.е. провести высокочастотную часть
, т.е. провести высокочастотную часть  с наклоном
с наклоном  (рис. 7.6).
(рис. 7.6).
По виду  можно записать
можно записать  . В нашем случае
. В нашем случае
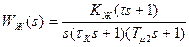 ,
,
где 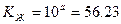 с-1 – коэффициент передачи желаемой системы; а = 1.75– значение
с-1 – коэффициент передачи желаемой системы; а = 1.75– значение  на оси
на оси  ;
;
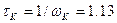 с – постоянная времени, соответствующая контрольной точке АК;
с – постоянная времени, соответствующая контрольной точке АК;
 = 0.32 с – дополнительная постоянная времени; b = 0.5 – значение
= 0.32 с – дополнительная постоянная времени; b = 0.5 – значение  на оси
на оси  .
.

Рис. 7.6. Желаемая ЛАЧХ
Полученную желаемую систему необходимо проверить в первую очередь на выполнение динамических показателей качества  .
.
Для этого сначала получим tf-модель  :
:
>> WJ=tf([56.23],[1,0])*tf([0.32,1],[1.13,1])*tf([],[0.024,1])
Transfer function:
17.99 s + 56.23
-----------------------------------
0.02712 s^3 + 1.154 s^2 + s
Оценим запас устойчивости желаемой системы:
>> margin(WJ); grid on
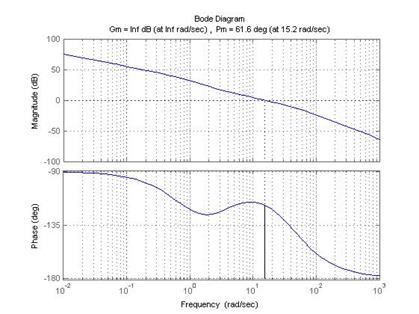
Рис. 7.7. ЛЧХ желаемой системы
Из рис. 7.7. видно, что система устойчива и запас по фазе равен  .
.
Передаточная функция замкнутой желаемой системы равна

или в tf-форме:
>> FJ=feedback(WJ,1)
Transfer function:
17.99 s + 56.23
----------------------------------------------------
0.02712 s^3 + 1.154 s^2 + 18.99 s + 56.23
Вычислим переходную характеристику для желаемой САУ
>> step(FJ); grid on
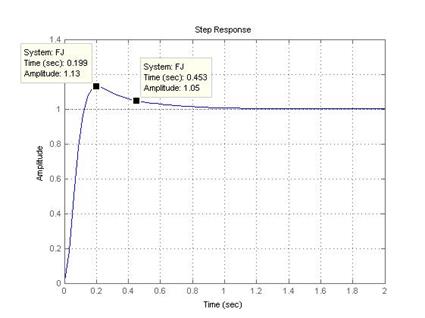
Рис.7.7. Переходная характеристика желаемой САУ.
Из данного переходного процесса можно определить перерегулирование  и быстродействие
и быстродействие 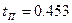 с
с  с.
с.
Если хотя бы одно из неравенств не выполнилось, то пришлось бы перестраивать  : например, увеличивать
: например, увеличивать 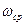 , если
, если  , или расширять длину среднечастотного участка, если
, или расширять длину среднечастотного участка, если 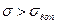 .
.
После выполнения всех требований к проектируемой системе определяется ПФ регулятора положения:
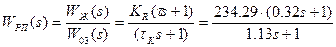 .
.
Далее можно переходить к этапу реализации регуляторов всех контуров управления.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 565; Нарушение авторских прав?; Мы поможем в написании вашей работы!