Широко используется в гидравлике также формула Блазиуса

(*)

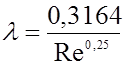применимость которой ограничена значениями числа .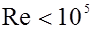

Алгоритм расчета установившегося турбулентного движения в трубе таков.

Задается диаметр трубы 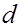, коэффициент кинематической вязкости жидкости 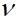и потребный объемный расход. По расходу и диаметру находим 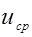, и, следовательно, число Рейнольдса 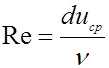. После этого по формуле Никурадзе находим коэффициент сопротивления 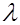, а затем и перепад давления 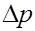на заданном участке трубы длины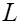

.

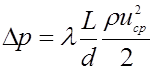По величине 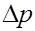найдем

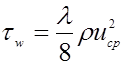
и

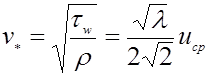
Остается воспользоваться формулой

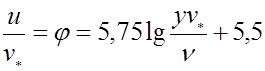
и задача может считаться решенной.

Наряду с приведенными выше полуэмпирическими формулами большую роль играют число эмпирические степенные профили скорости и сопротивления. К числу последних относится формула Блазиуса, которая представляет собой частный случай общей степенной формулы сопротивления

. (**)

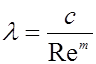Карман, из соображений размерности, показал, что степенному закону сопротивления Блазиуса соответствует степенной профиль скорости

,

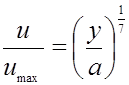получивший название закона одной седьмой.

Точно так же общей формуле (**) соответствует степенной закон скоростей .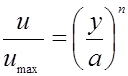

При этом связь между показателями степеней n и m имеет вид

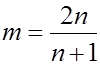
Изложенное выше относится лишь к движению жидкости в гладких трубах.

На практике приходится иметь дело с шероховатыми трубами и с трубами с неточной цилиндричностью внутренней поверхности - волнистостью.

Изучением влияния различного типа шероховатостей на сопротивление труб занимается гидравлика, в которой получены разнообразные практические формулы для определения сопротивлений применяемых в технике труб.

Говоря о шероховатости, представим что внутренняя поверхность трубы покрыта бугорками, имеющими вид зерен примерно одинакового диаметра. Обозначим через 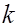высоту бугорка шероховатости (практически среднюю высоту) и условимся называть величину 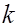, выраженную в миллиметрах абсолютной шероховатостью, а отношение величины 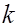к радиусу трубы a – относительной шероховатостью. В дальнейшем предполагаем, что относительная шероховатость сравнительно невелика и составляет 0.2 – 7 %.

Рассмотрение типичных для труб с указанной зернистой шероховатостью экспериментальных данных кривых сопротивления, показанных на рис. …… приводит к следующим выводам:

1) относительная шероховатость не влияет на критическое число Re_кр перехода ламинарного режима в турбулентный: для различных значений a/k кривые сходят с известной уже нам ламинарной прямой 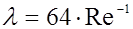при одном и том же числе Рейнольдса;

2) переходный режим тоже почти не зависит от относительной шероховатости;

3) чем меньше шероховатость, тем в большем диапазоне рейнольдсовых чисел наблюдается обычное турбулентное движение, соответствующее гладким трубам;

4) при тем больших числах Рейнольдса, чем меньше относительная шероховатость, коэффициент сопротивления перестает зависеть от числа Рейнольдса и определяется только относительной шероховатостью; при этом значения коэффициента сопротивления растут вместе с относительной шероховатостью.

Этим результатам можно дать наглядное теоретическое истолкование, если сопоставить высоту бугорка шероховатости 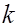с толщиной вязкого подслоя .

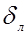Рассмотрим три следующие случая:

1. Первый предельный режим: бугорки шероховатости погружены в вязкий подслой (k«δ_л); наличие бугорков шероховатости не нарушает вязкого подслоя, бугорки обтекаются без отрывов и вихреобразований. В этом случае нет никакой разницы между гладкой и шероховатой трубами. Шероховатая труба является гидродинамически гладкой.

2. Второй предельный режим: бугорки шероховатости выходят за пределы вязкого подслоя (k»δ_л). Отрывное обтекание бугорков сводит тормозящее влияние поверхности трубы к сопротивлению плохо обтекаемых тел (бугорков шероховатости), которое не зависит от числа Рейнольдса и пропорционально скоростному напору набегающей жидкости. Этот режим можно назвать – режим развитой шероховатости.

3. Промежуточный режим, когда k имеет тот же порядок, что и δ_л. Этот режим является наиболее общим. Предыдущие режимы по отношению к нему являются предельными.

Имея в виду, что в общем случае сопротивление τ_w представляет отнесенное к единице поверхности суммарное сопротивление бугорков шероховатости, можно предположить справедливость формулы сопротивления (u_k – скорость на высоте бугорка)

,

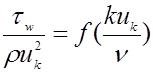где величина ku_k/ν играет роль рейнольдсова числа обтекания бугорков.

Отсюда следует, что

.

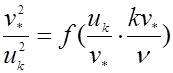Разрешая это уравнение относительно u_k/v_* получим:

.

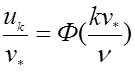Вид функции Ф неизвестен и определяется из опытов.

Воспользуемся линией вершин бугорков шероховатости (y=k, u=u_k) как недостающим граничным условием для определения постоянной интегрирования в выражении логарифмического профиля скорости. Тогда получим формулу распределения скоростей в шероховатой трубе

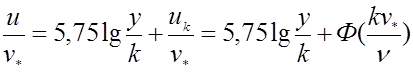
Применяя данную формулу к оси трубы, получим

.

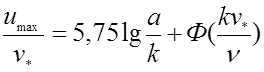
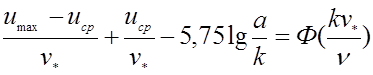Заменим здесь, как и ранее,

, ;

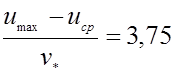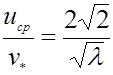тогда получим формулу сопротивления

.

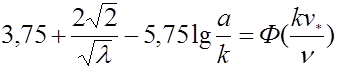Сравнивая между собой формулы для профиля скорости и для сопротивления убедимся, что для определения неизвестной функции Ф(kv_*/ν) имеются два не зависящих друг от друга пути. Один путь – по измеренным профилям скорости. Второй путь – по сопротивлению труб.

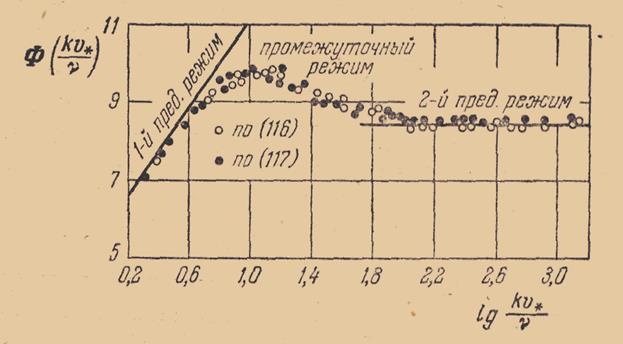
Используя экспериментальные исследования Никурадзе рассмотрим Ф(kv_*/ν) определенную двояким способом

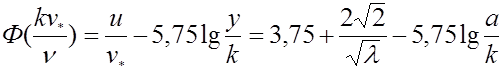
В первом предельном режиме, гда профиль скорости должен иметь вид логарифмического профиля, очевидно будет

.

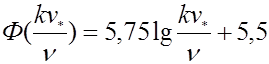Во втором предельном режиме

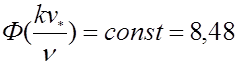
Как видно из графика, первый предельный режим имеет место до значений

, ,

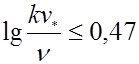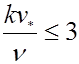что определяет границу использования гладких труб неравенством

.

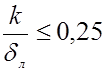Пользуясь определением толщины вязкого подслоя можем получить

,

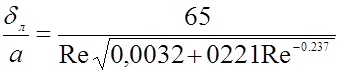что дает следующую оценку для области использования гладких труб:

.

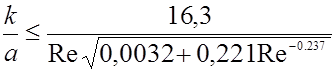Второй предельный режим определиться по тому же графику условием

,

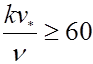
или

,

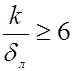что приведет к оценке границы области развитой шероховатости

.

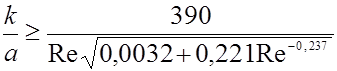Практически важен второй предельный режим, для которого функция Ф(kv_*/ν) сохраняет свое постоянное значение численно равное 8,48. В этом случае профиль скорости будет определяться формулой

.

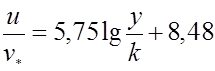Формула сопротивления, после простых преобразований примет вид

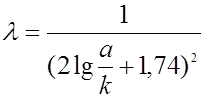
Дата добавления: 2015-06-27