Роль частиц в лазерной анемометрии

При определении скорости газового потока по измеренной Доплеровской частоте рассеянного излучения на частицах, находящихся в потоке, непременным условием является требование, чтобы частицы точно следовали за всеми изменениями потока. Это накладывает определенные требования на размер и концентрацию частиц в потоке: они должны быть достаточно малых размеров для того, чтобы полностью увлекаться потоком, и в то же время быть достаточных размеров для того, чтобы рассеяное излучение регистрировалось фотоприемником.

С уменьшением размера частиц резко уменьшается интенсивность рассеянного света; поэтому для оценки их пригодности в лазерной Доплеровской анемометрии необходимо точно знать оптические свойства дискретных рассеивателей, которые характеризуют амплитудными функциями рассеяния. Амплитудные функции рассеяния зависят от оптических и геометрических свойств частиц, угла рассеяния и угла азимута и находятся из решения уравнений Максвелла с заданными граничными условиями. Знание амплитудных функций рассеяния позволяет полностью определить параметры рассеянного излучения (поляризацию, амплитуду и фазу рассеянной волны).

Для лазерной анемометрии наибольший интерес представляют частицы с размером, сравнимым с длиной волны лазерного излучения. К сожалению, явный вид амплитудных функций рассеяния известен только для ограниченного числа случаев рассеяния: для сферических частиц с диаметром а < 0.03λ (случай Рэллеевского рассеяния) и для а > 0.03λ (область рассеяния Лоренца-Ми). Оказалось, что амплитудные функции рассеяния зависят только от трех параметров: относительного комплексного показателя преломления частиц, относительного размера частиц ρ=2πa/λ и угла пересечения 2θ.

Движущиеся вместе с газовым потоком частицы рассматриваются как приемники световых волн от неподвижного источника и одновременно как передатчики-ретрансляторы оптического излучения к неподвижному наблюдателю. Частота рассеянного излучения в точке наблюдения равна:

где ν – частота излучения источника; с – скорость света; u – проекция скорости частицы в направлении на точку наблюдения. Следовательно, Доплеровская частота, учитывая, что |u| << c, равна

В реальном эксперименте наблюдается рассеянное оптическое излучение частота, которого сдвинута на величину, прямо пропорциональную скорости рассеивающей частицы.

Таким образом, первая практическая задача, от решения которой зависит эффективность применения лазерного доплеровского метода измерения скорости, заключается в том, чтобы измерять не абсолютное значение оптической частоты, а радиочастоту равную разности двух оптических частот – опорной и рассеянной

Поэтому на практике применяется наложение двух рассеяных световых волн, в результате чего на фотоприемнике регистрируется сигнал с частотой, равной разности частот двух рассеянных волн:

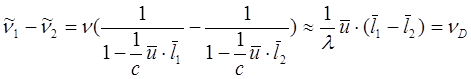
при |u|<<c.

Итак, Доплеровская частота сигнала на выходе фотоприемника зависит от длины волны лазерного излучения, скорости частиц и геометрии оптической системы. Эта формула представляет собой основное уравнение лазерной Доплеровской анемометрии и в принципе является очень точной (ее погрешность составляет менее 10^-5 %), так как ее параметры не зависят от свойств среды (температуры, давления и т.п.) и не требуют градуировки с помощью эталона –достаточно их точно рассчитать. Поэтому суммарная погрешность определения скорости газового потока определяется погрешностью измерения Доплеровской частоты.

Вторая практическая задача, заключается в выборе рассеивающих частиц и, соответственно, в выборе направления регистрации рассеянного излучения. Существует строгая теория рассеяния электромагнитных волн на сферических объектах. Наибольший интерес для доплеровских измерений представляют предельные случаи, а именно, когда длина волны много меньше размера рассеивающей частицы и когда соизмерима с размером частицы. С уменьшением размера частиц резко уменьшается интенсивность рассеянного света; поэтому для оценки их пригодности в лазерной Доплеровской анемометрии необходимо точно знать оптические свойства дискретных рассеивателей, которые характеризуют амплитудными функциями рассеяния. Амплитудные функции рассеяния зависят от оптических и геометрических свойств частиц, угла рассеяния и угла азимута и находятся из решения уравнений Максвелла с заданными граничными условиями. Знание амплитудных функций рассеяния позволяет полностью определить параметры рассеянного излучения (поляризацию, амплитуду и фазу рассеянной волны).

Для лазерной анемометрии наибольший интерес представляют частицы с размером, сравнимым с длиной волны лазерного излучения. К сожалению явный вид амплитудных функций рассеяния известен только для ограниченного числа случаев рассеяния: для сферических частиц с диаметром а < 0.03λ (случай Рэллеевского рассеяния) и для а > 0.03λ (область рассеяния Лоренца-Ми). Оказалось, что амплитудные функции рассеяния зависят только от трех параметров: относительного комплексного показателя преломления частиц, относительного размера частиц ρ=2πa/λ и угла пересечения 2θ.

Другая часть задачи по выбору светорассеивающих частиц заключается в выборе материала. Поскольку для металлических рассеивающих частиц направление распространения рассеянного поля обратное направлению падающей волны, а для диэлектрических частиц направление распространения рассеянного поля совпадает с направлением падающего поля. Таким образом, в зависимости от используемых частиц, конструкция анемометра должна обеспечивать работу, либо на обратном рассеянном поле, либо на прямом рассеянном поле. Либо обеспечивать работу в обоих направлениях.

Подробно теория доплеровского метода измерения скорости, а также анализ других оптических схем и систем обработки сигнала ЛДА изложены в книгах [1-2].

Аналитическое описание работы ЛДА

Принцип работы ЛДА основан на эффекте Доплера, суть которого заключается в зависимости частоты излучения света, отражённого или рассеянного движущимся объектом, от скорости его движения.

Если на объект, движущийся со скоростью U, направить монохроматическое излучение с частотой 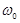(рис. 1а), то отражённое (рассеянное) излучение, вследствие эффекта Доплера, будет иметь частоту 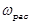, которая отличается от частоты падающего излучения.

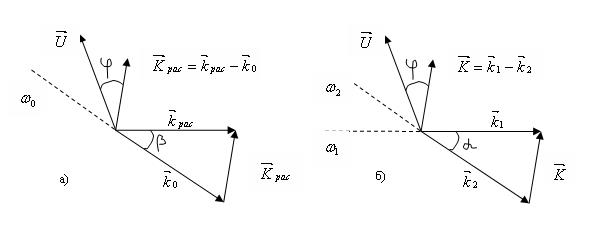
Рис. 3. Взаимное расположение векторов рассеяния в схеме с одним (а) и двумя (б) зондирующими пучками.

Доплеровский сдвиг частоты (д.с.ч.) определяется выражением [1, 2]:

,

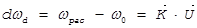где - разностный волновой вектор, 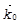волновой вектор падающего излучения, 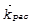- волновой вектор рассеянного излучения.

С учётом введённых на рис.3 обозначений

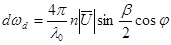, (5)

где 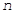- показатель преломления среды, - длина волны падающего излучения в вакууме.

Характерной особенностью выражения (5) является линейная зависимость д.с.ч. от величины скорости, причём коэффициент пропорциональности зависит от геометрии схемы (углов и ) и оптических свойств среды.

Рассмотрим теперь схемy с двумя зондирующими пучками, имеющими волновые векторы 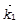и 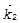и близкие частоты и (рис. 5б). Разность д.с.ч. волн рассеянных в одном направлении двумя пучками определяется соотношением [1,2]:

, (6)

где 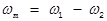- разностная частота, которая по причине, поясняемой ниже, часто называется частотой модуляции, 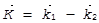- вектор чувствительности, модуль которого равен

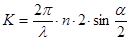. (7)

Здесь 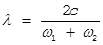, n – показатель преломления среды, 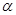- угол между пучками.

Отметим, что разность частот (6) не зависит от направления наблюдения. Такие схемы называются дифференциальными.

При 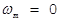, а также обозначений, введённых на рис. 3б, имеем:

. (8)

Формула (8) позволяет рассчитывать д.с.ч. при известной скорости объекта и заданном направлении падающих и рассеянных пучков. Из них же можно найти и величину проекции вектора скорости 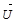на выбранное направление, определяемое векторам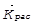и и при известной величине .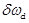

Принцип работы дифференциальной схемы ЛДА можно объяснить и не используя явным образом эффект Доплера. Суть этого объяснения заключается в следующем: движущаяся частица рассеивает излучение в интерференционном поле, которое образуется в области пересечения двух когерентных пучков.

Для того чтобы показать эквивалентность обоих подходов рассмотрим картину интерференции. Для простоты будем считать, что пересекаются две плоские монохроматические волны, электрические векторы которых запишем в следующем виде:

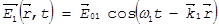
где 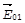, и 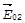- векторы амплитуды падающих волн.

Усреднённая за промежуток времени τ 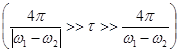интенсивность света будет равна

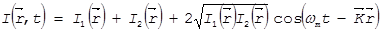
Таким образом, в области пересечения двух когерентных монохроматических пучков с разными частотами образуется периодически меняющееся во времени распределение интенсивности, эквивалентное бегущей световой решётке. Направление движения решётки и ее период определяются вектором чувствительности , а скорость движения светлых и тёмных полос определяется разностью частот интерферирующих волн.

Если , то есть частоты интерферирующих волн совпадают, то имеет место стационарная интерференционная картина. Видность этой интерференционной картины V равна:

. (9)

При равенстве интенсивностей интерферирующих волн видность максимальна и равна 1.

Период изменения интерференционных максимумов и минимумов интенсивности в плоскости, перпендикулярной биссектрисе угла 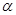равен:

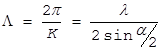(10)

Чем меньше угол между падающими пучками, тем больше период интерференционной картины. Так, пр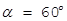и и мкм период 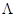= 0,63 мкм, а при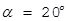 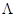= 109 мкм.

Пусть в области пересечения пучков движется малая в простейшем случае сферическая (радиуса r < 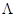) частица со скоростью, характеризующейся вектором 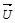. Мощность рассеянного этой частицей излучения зависит от её местоположения, размера и оптических характеристик. Если частица находится в центре светлой интерференционной полосы, она рассеивает максимальную мощность, а если в центре тёмной полосы - минимальную. Особенности работы ЛДА с большими частицами (r 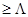) рассмотрены в работе [2].

Мощность, рассеянную частицами, движущимися со скоростью U через измерительный объем, можно записать в следующем виде:

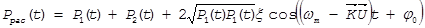, (11)

где 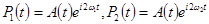, A(t) – медленно меняющаяся (по сравнению с 1/ω_1,2) случайная компонента. Коэффициент 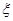обычно принимает значения от 1 до 10 ^-2 в зависимости от условий согласования амплитуд, фаз и состояния поляризации рассеянных волн в пределах приёмной апертуры, а также от величины отношения .

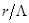Из уравнения (11) видно, что усредненная по времени 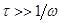рассеянная мощность меняется с частотой равной:

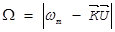, (12)

В случае (частоты зондирующих пучков равны) регистрация д.с.ч, не даёт информации о знаке скорости (12)

Рассмотрим случай бегущей интерференционной картины . Если частица движется в ту же сторону, что и интерференционные полосы, то ; если частица движется навстречу полосам, то . Таким образом, ЛДА чувствителен не только к величине проекции скорости частицы на вектор чувствительности, но и к знаку проекции скорости.

Блок-схема ЛДА. Характеристика основных элементов

Рассмотрим в общем виде основные функциональные блоки ЛДА, которые позволяют представить в целом работу измерителя скорости, его возможности и требования, предъявляемые к различным его элементам.

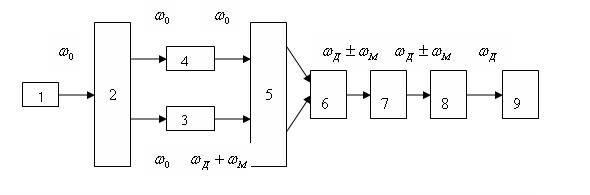
Рис. 4. Блок-схема дифференциального ЛДА с частотной модуляцией пучка. 1 – лазер, 2 – блок формирования зондирующих пучков, 3 – однополосный модулятор, 4 – линия задержки, 5 – блок передающей оптики, 6 – исследуемый объект, 7 – блок приемной оптики, 8 – блок выделения д.с.ч., 9 – устройство обработки сигнала.

Блок-схема ЛДА, построенного по дифференциальной схеме, изображена на рис. 4. Источннком когерентного излучения является лазер, как правило непрерывного действия, хотя в некоторых случаях возможно применение и импульсных лазеров. Излучение лазера в блоке (2) делится на два пучка, один из которых в знакочувствительных ЛДА пропускается через однополосный модулятор (3), сдвигающий частоту 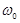излучения на величину 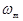(которая потому и называется частотой модуляции). Для сдвига частоты часто используется акустооптический эффект. Один из пучков в некоторых измерителях проходит через линию задержки (4) для выравнивання длины оптического пути. Блок передаюшей оптики (5) направляет зондирующие пучки на исследуемый объект (6), содержащий движущиеся светорассеивающие частицы. Для транспортировки излучения к измерительному объекту часто используют оптические волноводы. Для увеличения светосилы метода рассеянный свет собирается приёмной оптикой (7) и направляется на блок выделения д.с.ч. (8). Выделенный сигнал, содержащий информацию о скорости движения частиц в области пересечения зондирующих пучков, обрабатывается в блоке 9.

Дадим краткую характеристику основных элементов ЛДА и рассмотрим требования, предъявляемые к ним.

1) Лазер. Основными параметрами, характеризующими лазер, как источник излучения в ЛДА, являются длина волны излучения , спектp излучения, тип колебаний и мощность. Выбор конкретного типа лазера обуславливается задачей, для которой предназначен ЛДА. Например, СО₂ лазеры обладают большой мощностью (до нескольких десятков Вт в режиме непрерывноro излучения), длина волны излучения которых 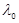=10,6 мкм лежит в инфракрасной области спектра. Такое излучение сильно поглощается жидкостями, что исключает возможность их применения для исследования гидродинамических потоков. С другой стороны, большая мощность CO₂ лазеров позволяет создавать ЛДА, которые предназначены для исследования воздушных потоков, содержащих аэрозоли, на расстояниях до нескольких километров.

Длина волны 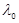определяет минимальный размер области пересечения зондирующих пучков, то есть величину измерительного объёма. Даже если пучки фокусируются и пересекаются в перетяжках, то поперечный размер перетяжки ограничен дифракционным пределом, который тем меньше, чем меньше 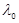. Большая локальность измерений особенно важна при решении таких задач, как исследования микроструктуры турбулентных потоков, измерение скорости течения в микрокапиллярах и т.п. Важным параметром лазерного излучения является его спектр, т.е. временная когерентность. Для получения хороших характеристик ЛДА, как по пространственному разрешению, так и по отношению сигнал/шум, излучение лазера должно иметь самый низкий поперечный тип колебаний ТЕМ₀₀. При измерении малых скоростей лазеры могут работать на нескольких npoдольных типах колебаний, когда д.с.ч. меньше частотного игнтервала между этими типами колебаний. При измерении больших скоростей, как правило, нужны одночастотные лазеры.

Мощность лазеров определяет чувствительность установки. В случае большой концентрации рассеиваюших частиц, что характерно, например, для двухфазных потоков и твердых тел с шероховатыми nоверхностями, возможно применение лазеров небольшой мощности (около единиц мВт). Как правило, в этом случае используются получившие широкое распространение He-Ne или полупроводниковые лазеры. Если ЛДА применяется для исследования структуры потоков газа с малой концентрацией светорассеивающих частиц, то здесь необходимо использовать лазер большой мощности, наприиер, аргоновый или СО₂.

2) Блок формирования зондирующих пучков может быть устроен по-разному. Исходный пучок можно разделить на два по амплитуде или по фрон­ту. В первом случае, как правило, нспользуется делительный кубик, плас­тинка или полупрозрачное зеркало. Во втором случае используются призмы или маски той или иной формы.

3) В качестве однополосного модулятора, осуществляющего сдвиг частоты излучения в одном из двух зондирующих пучков (в знакочувствительных ЛДА), чаще всего используется акусто- или электрооптические преобразователи и вращающиеся дифракционные решётки.

4) Линия задержки предназначена для выравнивания длин оптических путей зондирующих пучков. Допустимая разность хода определяется длиной когерентности 1_k используемого лазера. Для эффективного выделения д.с.ч. необходимо, чтобы разность хода была меньше l_k. Так как 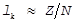, где Z - длина резонатора, а N - число одновременно генерируемых продольных мод, то в большинстве cистем ЛДА это выравнивание не представляет серьёзных проблем. Зачастyю линии задержки вообще отсутствуют.

5) Блок передающей оптики осуществляет сведение зондирующих пуч­ков в область, где производятся измерения. В тех случаях, когда важна локальность измерения, пучки специально фокусируются. В простейшем случае этот блок представляет собой фокусирующую линзу или объектив. В некоторых случаях линза или объектпв ставится в каждый пучок, а сведение пучкoв в область измерения осуществляется поворотными зеркалами.

7) Блок приёмной оптики, как правило, представляет собой линзу или объектив, иногда с переменной апертурой. В случаях, когда д.с.ч. выделяется из света, расееянного назад (например, при измерении скорости движения оптически непрозрачного твёрдого тела), функции приёмной оптики может выполнять передающая линза. Задача блока приемной оптики состоит в том, чтобы собрать на фотоприемник рассеянное излучение из измерительного объема в возможно большем телесном угле.

8) Функции блока выделения д.с.ч. выполняют фотоприёмники (ФП): фотодиоды (ФД) или фотоумножители (ФЭУ), обладающие большой чувствительностью и хорошим быстродействием. При выборе конкретного типа ФЭУ или ФД принимают во внимание все его характеристики: коэффициент усиления, спектральную и частотную характеристики, темновой ток, пороговую чувствительность. Особенно тщательный выбор ФП делается при измерениях скорости движения слабо рассеивающих сред, когда регистрация рассеянного излучения ведётся в режиме счета фотонов. В дифференциальнык схемах ЛДА ФП осуществляет выделение д.с.ч. путём прямого фотодетектирования колебаний интенсивности рассеянного света,преобразуя их в колебания силы фототока. Частотно модулированный выходной ток ФП и является выходным сигналом ЛДА.

9) устройство обработки сигнала преобразует информацию, содержашуюся в фототоке, в удобную для пользователя форму. При этом используются либо аналоговые, либо цифровые методы, либо их комбинация. Более подробно охарактеризуем эти методы после того, как рассмотрим свойства сигнала ЛДА.

Дата добавления: 2015-06-27