Машинное представление графа

И ШИРИНУ НА ГРАФАХ.

АЛГОРИТМЫ ПОИСКА В ГЛУБИНУ

Нерекурсивный DFS

void DFS()

{ stack<int> s; s.push(start); while (!s.empty()) { int v = s.top(); s.pop(); for (int i = 0; i < edges[v].size(); ++i) { if (mark[edges[v][i]] == 0) { s.push(edges[v][i]); mark[edges[v][i]] = 1; } } }}

Методические указания к практическим занятиям

по курсу "Дискретная математика".

Для студентов, обучающихся по направлению

230200 - "Информационные системы "

Воронеж 2011

УДК 51(075); 681.3.06

Алгоритмы поиска в глубину и ширину на графах: Методические указания к практическим занятиям по курсу "Дискретная математика" /Воронеж. гос. технол. акад.: Сост. Ю.В. Бугаев, И.Ю. Шурупова, О.Ю. Никифорова. Воронеж, 2001. с.

Излагаются способы машинного представления графа и алгоритмы поиска в глубину и ширину на графах. Для каждой темы приведениы варианты заданий для самостоятельной работы. Задания разработаны в соответствии с требованиями ГОС ВПО подготовки инженеров по специальности 071900 - "Информационные системы и технологии". Они предназначены для закрепления теоретических знаний дисциплины цикла ЕН.

Библиогр.: 6 назв.

Составители: доцент Ю.В. БУГАЕВ,

доцент И.Ю. ШУРУПОВА,

ассистент О.Ю. НИКИФОРОВА

Научный редактор профессор В.В. СЫСОЕВ

Рецензент доцент М.Г.ЗАВГОРОДНИЙ

Печатается по решению

редакционно-издательского совета

Воронежской государственной технологической академии

Ó Бугаев Ю.В.,

Шурупова И.Ю.,

Никифорова О.Ю., 2001

Ó Воронежская государственная технологическая

академия, 2011

Цель занятий – изучение способов представления графа и простейших алгоритмов на графах, и использование этих алгоритмов при программировании задач на графах. Данное методическое указание рассчитано на 3 практических занятия (6 часов).

Приведем вначале сравнительную характеристику существующих способов представления графа в памяти ЭВМ, их достоинства и недостатки.

Рассмотрим конечный граф G =(V, E), где | V |= n, | E |= m.

Матрица инциденций.

Ориентированный граф задается прямоугольной матрицей B (n ´ m), элементы которой определяются по правилу:

где a – любое натуральное число, отличное от 1. У неориентированного графа оба элемента матрицы, соответствующие вершинам, инцидентным ребру e_j, равны 1.

Это представление графа является самым неудобным, так как объем занимаемой памяти равен n×m единиц, причем в каждом столбце только две ненулевые ячейки. Кроме нерационального использования памяти недостатком этого способа представления является неудобный доступ к информации. Например, для ответа на вопросы:

а) существует ли ребро (дуга) (v_i, v_j);

б) к каким вершинам ведут ребра (дуги) из вершины v_i

требуется, в худшем случае, перебор n×m элементов, т.е. порядка n×m шагов алгоритма. От этого недостатка свободен следующий способ представления графа.

Матрица смежности.

Элементы квадратной матрицы A (n ´ n) определяются следующим образом:

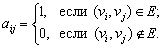
Проверка существования ребра (дуги) (v_i, v_j) осуществляется за один шаг, в отличие от матрицы инциденций, однако, проверка свойств графа на основе такого представления требует, в худшем случае, порядка n ² шагов алгоритма. При этом способе объем неиспользованной памяти по-прежнему велик.

Заметим, что для сокращения объема используемой памяти возможно использование 1-го бита для хранения элемента a_ij, но при этом, выигрывая в памяти, мы затрудняем доступ к информации. В этом случае придется применять операции для работы с битами информации, используя различные маски.

При работе со взвешенными графами для хранения весов ребер (дуг) требуются дополнительные одномерные массивы размера m (для случая матрицы инциденций) или матрицы размера n ´ n (для случая матрицы смежности). Это обстоятельство делает неприемлимым использование матрицы смежности для взвешенных графов, так как количество неиспользованных единиц памяти увеличивается в k раз, где k – число весов ребер (дуг).

Съэкономить объем используемой памяти можно, применяя представление графа в виде

Таблицы ребер.

Она представляет собой матрицу размером m ´2, каждая строка которой содержит вершины инцидентные i -му ребру (i -ой дуге). Для работы со взвешенными графами нужно добавить к матрице столбцы, соответствующие весам ребер (дуг).

Однако, этому способу представления графа присущ тот же недостаток, что и матрице инциденций, - неудобство доступа к информации, хотя число шагов при поиске ребра здесь значительно меньше (порядка m). Поиск можно ускорить, введя лексикографический порядок в упорядочении пар и применяя двоичный поиск.

Наиболее удобной и экономичной формой представления графа являются

Списки инцидентности.

Для каждой вершины v_i Î V создается список записей, характерезующих ребра (дуги), инцидентные этой вершине. Таким образом, это представление использует объем памяти порядка (n + m), поиск вершины смежной с данной требует порядка (n + m) шагов, проверка свойств графа осуществляется за число шагов порядка. Поэтому остановимся подробнее на этом способе задания графа.

Каждая запись содержит две части: информационную и ссылочную. В информационную часть включаются поля:

а) вершина v_j, смежная с вершиной v_i;

б) веса ребер (дуг) при работе со взвешенными графами;

в) другая вспомогательная информация о ребре (дуге), если это необходимо для работы с графом.

Ссылочная часть содержит:

а) ссылку на следующую запись списка;

б) ссылку на предыдущую запись списка (для двунаправленных списков);

в) ссылку на запись, содержащую вершину v_i, в списке инцидентности вершины v_j (для неориентированного графа).

Типы «запись» и «ссылка на запись» должны быть предварительно описаны в программе. Например, описание

type ref = ^Ù Elem;

Elem = record

num: integer;

ves: array [1.. kv] of real;

sled, pred, ref_vi: ref;

end;

определяет запись, характерезующую ребро взвешенного неориентированного графа с числом весов kv, и ссылку на эту запись (типизированный указатель). В данном примере используется двунаправленные списки.

Ссылки на первую запись каждого списка хранятся в массиве, размер которого равен числу вершин графа. В программе должна быть описана переменная типа «массив», элементы которого имеют тип «ссылка на запись». Например,

var mas_ref: array [1.. n] of ref;

Если вершина v_i является изолированной, то mas_ref [v_i]= nil.

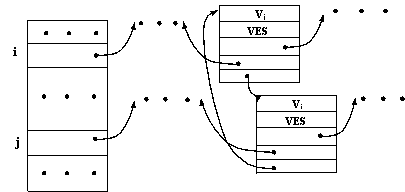
Структуру представления графа в памяти ЭВМ можно схематично представить следующим образом:

Рис. 1

На этом рисунке изображены фрагменты списков инцидентности неориентированного графа, соответствующие ребру графа 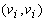. У ориентированного графа в каждой записи будет отсутствовать третье ссылочное поле, и не будет дублирования в списке инцидентности конечной вершины дуги.

Например, неориентированный граф

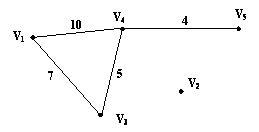
Рис. 2

имеет cледующее представление в памяти

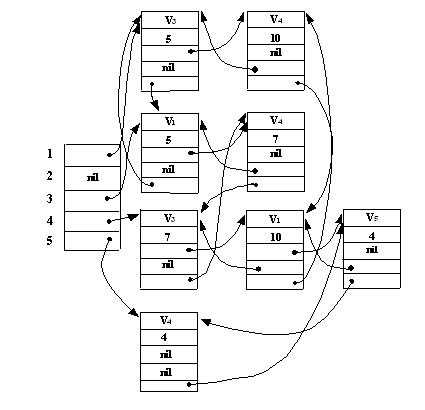
Рис. 3

Для ориентированных графов могут формироваться как списки вершин, следующих за текущей, так и предшествующих ей вершин.

Для формирования машинного представления графа необходимо сформировать список инцидентности для каждой вершины графа и заполнить массив ссылок на эти списки. Формирование списка инцидентности может осуществляться по принципу стека (LIFO), когда новая запись включается в начало списка, или по принципу очереди (FIFO), когда новая запись ставится в конец списка.

Напомним, что для включения записи в список нужно выделить область динамической памяти, соответствующую размеру записи, и заполнить ее поля.

При работе с графом часто требуется выполнить действия, изменяющие его структуру. К ним относятся:

1. Добавление ребра (дуги) (v_i, v_j) в граф G.

Для этого нужно:

а) добавить запись с вершиной v_j в список инцидентности вершины v_i;

б) для неориентированного графа добавить запись с вершиной v_i в список инцидентности вершины v_j.

2. Удаление ребра (дуги) (v_i, v_j) из графа G (осуществляется аналогично добавлению ребра (дуги)).

3. Удаление вершины v_i из графа G.

Для этого нужно удалить все ребра (дуги) инцидентные вершине v_i (т.е. удалить все записи из списка вершины v_i, а для неориентированных графов – и соответствующие записи из списков смежных с ней вершин) и изменить ссылку в массиве ссылок на списки инцидентности mas_ref [v_i]= nil.

Часто кроме изменения структуры графа для более эффективной работы алгоритмов требуется сортировка (упорядочение) списков инцидентности. При этом применяются известные алгоритмы сортировки, следует лишь заметить, что при изменении порядка записей в списке изменяются только поля sled, pred в записях списка.

Ввод графа осуществляется из текстового файла одного из двух видов: «таблица смежности» или «таблица ребер». Такие файлы по-разному формируются и интерпретируются для неориентированных и ориентированных графов: для неориентированного графа задаются ребра графа, а для ориентированного – дуги. То есть, ребро неориентированного графа задается один раз, а соответствующие ему записи автоматически включаются в списки инцидентности обоих его концов.

Файл «таблица смежности» состоит из блоков, соответствующих вершинам графа. Каждый блок имеет следующую структуру:

начальная вершина: список смежных с ней вершин

соответствующие ребрам веса

Количество строк с весами ребер равно kv, число вершин списка равно числу весов в строках. Блоки в таком файле могут располагаться в произвольном порядке, причем, если вершина не является начальной ни для одного ребра (дуги) или ребро уже включено в список инцидентности другого его конца, то соответствующий ей блок может отсутствовать в файле.

Например, файл «таблица смежности» графа, изображенного на рис.2 имеет вид

v₁: v₃ v₄

5 10

v₃: v₄

v₄: v₅

4,

а ориентированный граф

Рис.4

задается «таблицей смежности»

1: 2 3

2: 3

3: 1

Файл «таблица ребер» имеет следующую структуру:

начальные вершины ребер (дуг)

конечные вершины ребер (дуг)

веса ребер (дуг)

Также как и для «таблицы смежности» количество элементов в каждой из строк должно быть одинаковым, а число весов равно kv. Если строка данных не умещается на экран монитора, то для удобства просмотра файла можно перенести оставшиеся части ниже в том же порядке, отделив одну часть от другой пустой строкой.

Например, файл «таблица ребер» графа, изображенного на рис.2 имеет вид.

v₁ v₁ v₄ v₄

v₄ v₃ v₃ v₅

10 5 7 4

Вывод списков инцидентности графа на экран или в файл осуществляется в соответствии со структурой аналогичной файлу «таблица смежности». При этом просматривается список каждой вершины, если он непуст, то выводится: СП, затем в скобках вершина,:, список вершин смежных с ней. Например, выводимая информация имеет вид:

а) для графа (рис.2)

СП(v₁): v₃ v₄

СП(v₃): v₁ v₄

СП(v₄): v₁ v₃ v₅

СП(v₅): v₄;

б) для графа (рис.4)

Списки следования: Списки предшествования:

СП [1]: 2 3 СП [1]: 3

СП [2]: 3 СП [2]: 1

СП [3]: 1 СП [3]: 2 1.

Задание для самостоятельной работы.

I. Написать и отладить программу в соответствии с вариантом задания №1 (см. приложение). Такая программа должна содержать:

1) ввод исходного графа из файла заданного вида и формирование для него списков инцидентности;

2) подсчет и вывод количества вершин и ребер (дуг), вывод списков инцидентности исходного графа;

3) выполнение индивидуального задания варианта и вывод его результатов.

II. Продемонстрировать работу программы на контрольном примере.

III. Текст программы, граф и исходный файл контрольного примера, результаты работы программы оформить в отчет.

Дата добавления: 2015-06-27