Сила, действующая на ток в магнитном поле. Закон Ампера

Преломление линий магнитной индукции (самостоятельно).

Согласно закону, установленному Ампером, на элемент тока действует в магнитном поле сила

(1)

k – коэффициент пропорциональности;

i – сила тока;

В – магнитная индукция в том месте, где помещается элемент dl.

Величина силы (1) вычисляется по формуле

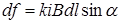, (2)

где α – угол между векторами и (рис. 1а). Направлена сила перпендикулярно к плоскости, в которой лежат векторы и .

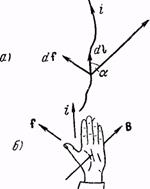
Рисунок 1 – Определение направления силы Ампера

Направление силы, действующей на ток, удобно определять с помощью так называемого правила левой руки.

Если расположить левую руку так, чтобы вектор «вонзался» в ладонь, а четыре сложенные вместе пальца были направлены вдоль тока, то отставленный в сторону большой палец укажет направление силы (рис. 1б).

Применим закон Ампера для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами b (рис. 2), то каждый элемент тока i₂ будет находиться в магнитном поле, индукция которого

Угол α между элементами тока i₂ и вектором прямой. Следовательно, на единицу длины тока i₂ действует сила

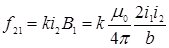. (3)

Для силы f₁₂, действующей на единицу длины тока i₁ получается аналогичное выражение. С помощью правила левой руки легко установить, что при одинаковом направлении токов они притягивают друг друга, а при различном – отталкивают.

В СИ закон Ампера имеет вид

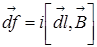(4)

Соответственно

df = IB dl sin a.

В гауссовой системе формула (46.1) имеет вид

dl = — i [dl В]

с

(46.5)

(46.6)

(см. замечание на стр. 126).

В гауссовой системе магнитная индукция в вакууме совпадает с Н, вследствие чего в этом случае закон Ампера можно записать следующим образом:

df = -j«[dlHJ. (45.7)

§ 47. Сила Лоренца

Проводник, по которому течет ток, отличается от про­водника без тока лишь тем, что в нем происходит упо­рядоченное движение носителей заряда. Отсюда напра­шивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, а уже от этих зарядов действие передается проводнику, по которому они пере­мещаются. Этот вывод подтверждается целым рядом опытных фактов и, в частности, тем, что пучок свободно летящих заряженных частиц, например электронный пу­чок, отклоняется магнитным полем.

Согласно (46.4) на элемент тока d\ действует в маг­нитном поле сила

(47.1)

Заменив id\ через Sj dl [см. формулу (40.G)], выраже­нию закона Ампера можно придать вид

где dV — объем проводника, к которому приложена си­ла df. Разделив df на d V, получим «плотность силы», т. е. силу, действующую на единицу объема проводника:

*ед.о6 = ПВ]. (47.2)

Подставив в эту формулу выражение (40.7) для j, найдем, что

f«. об = tie' [uB].

Эта сила равна сумме сил, приложенных к носителям, заключенным в единице объема. Таких носителей п, сле­довательно, на один носитель действует сила, равная?ед. ос/" = е'[иВ]. Таким образом, можно утверждать, что на заряд е', движущийся со скоростью v в магнитном поле В, действует сила

f = e'[vB]. (47.3)

Силу (47.3) называют силой Лоренца или ло-ренце вой силой¹).

') Часто лоренцевой силой называют сумму электрической и магнитной сил, действующих на заряд:

f = e'E -f e' [vB]. 158

В гауссовой системе ее выражение имеет вид

f=4f^vBl> (47.4)

\i

причем для вакуума В можно заменить на Н, Модуль лоренцевой силы равен

(47.6)

где а — угол между векторами v и В. Следовательно, за­ряд, движущийся вдоль линий магнитного поля, не испы­тывает действия силы.

Направлена сила Лоренца перпендикулярно к плос­кости, в которой лежат векторы v и В. Если заряд е' по­ложителен, направление

силы совпадает с на- '

правлением вектора [vB]. т

В случае отрицательного I

е' направления векторов /~~Л__ - х^\ _

f и [vB] противоположны (+) *"'^u JC/ **

(Рис. 86). Х| X

Поскольку сила Ло- в I В

ренца всегда направлена V

перпендикулярно к ско­
рости заряженной ча­
стицы, она работы над р^нс- ⁸⁶-

частицей не совершает.

Следовательно, действуя на заряженную частицу по­стоянным магнитным полем, изменить ее энергию нельзя.

При получении выражения. (47.3) для силы Лоренца из формулы (47.1) мы считали, что носители заряда в проводнике движутся со скоростью упорядоченного дви­жения и. Однако даже в отсутствие тока носители за­ряда находятся в хаотическом тепловом движении. Сред­нее (по носителям) значение вектора скорости этого движения vq равно нулю:

Поэтому и результирующая сил (47.3), действующих на носители, заключенные в элементе проводника Д/, при отсутствии тока также равна нулю:

oJBj-O. (47.6)

При возникновении тока скорость носителя стано-ится равной v = v₀ + и. В этом случае

Af = S e' [(у„ + и) В] = 2 e^r [v₀B] + S в' [иВ].

Первая сумма в этом выражении в соответствии с (47.6) равна нулю. Вторая сумма по существу совпадает с (47.2). Таким образом, действующая на ток амперова сила слагается из лоренцевых сил, обусловленных упо­рядоченным движением носителей заряда.

Сила, действующая на ток в магнитном поле, имеет значение (47.1), независимо от того, покоится провод--лк с током или перемещается относительно магнитного -оля. В этом легко убедиться, воспользовавшись выра­жением (47.3) для силы Лоренца. Пусть провод, по ко­торому течет ток, движется со скоростью v, а электрон, являющийся носителем заряда, имеет относительно про-пода скорость и. Тогда электрон движется относительно поля со скоростью v + u и на него будет действовать сила

f_ = - e [(v + и), Е]=-е [vB]- е [иВ],

а на участок провода — сила

4- = - e [vB] dN-e [UB] dN,

где dN — число электронов в элементе тока dl, a u — средняя скорость их движения относительно проводника. Провод в целом нейтрален — он образован непод­вижными ') положительными ионами и свободно движу­щимися электронами (см. т. 1, § 139, металлические кри­сталлы). Положительные ионы движутся вместе с про­водом со скоростью v, так что на каждый из них действует сила

f ₊ = e [vB].

Число ионов в элементе тока dl такое же, как число электронов. Следовательно, на ионы, содержащиеся в элементе dl, действует сила

') В действительности ионы не неподвижны, а колеблются около узлов кристаллической решетки. Однако sto не существенно, так как их средняя скорость относительно решетки равна нулю.

Элемент провода длины dl испытывает действие си­лы, равной сумме сил df_ и dt₊, которая, как легко ви­деть, имеет значение

tf = df_ + df₊--e[UB]dtf.

Полученное нами выражение эквивалентно формуле (47.1). В него не входит скорость проводника v. Таким образом, закон Ампера имеет одинаковый вид и для покоящегося и для движущегося проводника.

§ 48. Контур с током в магнитном поле

Пусть прямоугольный плоский контур с током по­мещается в однородном магнитном поле. Если контур ориентирован так, что вектор В параллелен его плоско­сти (рис. 87), то стороны, имеющие длину Ь, не будут

I

1 1 ^J	X^f V^х4"	.. в t Г -^	>^ХВ
	иГ Г^Х
			Ь 1 ' з
	•«о ^а=ьп Рис. 87.		^ff* Рис. 88.

испытывать действия сил, так как для них в формуле (46.5) sin а = 0. На левый участок будет согласно за­кону Ампера действовать сила / = iBa, направленная за чертеж, на правый участок — такая же по величине, но противоположно направленная сила /'. Эти силы обра­зуют пару, момент которой равен

М = f Ь = /Baft.

Учитывая, что ab равно площади контура S, а iS дает величину магнитного момента р_т, можно написать

М = _РтВ.

(48.1)

Эта формула совпадает по существу с формулой (39.3).

Момент М стремится повернуть контур так, чтобы

его магнитный момент р_т установился по направлению

поля В. Такая ориентация контура показана на рис. 88.

[[ И. В. Савельеп, т. II

В этом случае /, = f_s =* iBa, /₂ = f₄ = iBb. Направления всех сил лежат в плоскости контура. Легко видеть, что вращательный момент в этом случае не возникает. По­скольку поле однородно, равнодействующая сил равна нулю; силы лишь растягивают контур, но сместить его не могут. Заметим, что если повернуть контур на 180° (или изменить направление поля на обратное), то на­правления всех сил изме­нятся на противополож­ные, и они будут не рас­тягивать, а сжимать кон­тур.

Покажем, что фор­мула (48.1) справедлива и для плоского контура

%

d ff) •	ь?			В
\*^at	dh		I
v —	X f^of?

Рис. 89.

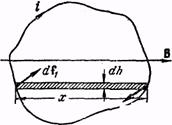
произвольной формы. Ра­зобьем площадь кон- -* _в тура на узкие параллель-»- ные направлению вектора В полоски шириной dh (рис. 89, а). На элемент контура dl\ действует си­ла dfi = iB dl\ sin «i, на­правленная за чертеж. На элемент dl₂ действует сила dj₂ = iB dl_z sin 02, имеющая противоположное направле­ние. Как видно из рис. 89, б, dli sin «i = dl₂ sin a₂ — dh — ширине полоски. Следовательно, силы df_t и df₂ одина­ковы по величине и образуют пару, момент которой ра­вен

dM = IB dh • b,

где 6 — длина полоски. Произведение b dh дает площадь полоски dS. Таким образом,

dM = iB dS.

Беря попарно силы, приложенные к противолежащим элементам контура, и суммируя их моменты, получим ре­зультирующий момент, действующий на контур;

М--

dM - iB dS=iSB - p_mB.

Итак, мы снова пришли к формуле (48.1).

При произвольной ориентации контура ^рис, 90)
магеттную нндукщмю В можно разложить на составляю­
щие: bi — перпендикулярную и Вц — параллельную пло­
скости контура, и рассматривать действие каждой со­
ставляющей отдельно. Составляющая Bj_ будет обуслов­
ливать силы, растягивающие или сжимающие контур.
Составляющая Вц, величина которой равна В sin а (в, —
угол меясду р„ и В), приведет к возникновению враща­
тельного момента, который можно вы­
числить по формуле (48.1): />в„

М = Рт^В\\ — РтВ sin а. (48.2)

Принимая во внимание взаимную ориентацию векторов М, р_т и В, фор­мулу (48.2) можно записать в виде

М = [р„В]. (48.3)

Для вакуума в гауссовой системе эта фор»
мула имеет вид Рис. 90.

М=[р_шН]. (48.4)

Для того чтобы угол а между векторами р_т и В уве­личить на da, нужно совершить против сил, действую­щих на контур в поле, работу

4А = М da. = p_mB sin a da. (48.5)

Поворачиваясь в иервоначальвое положение, контур может возвратить ааяраченную на его поворот работу, совершив ее над какями-лабо телами. Следовательно, работа (48.5) идет на увеличение энергии W, котарда обладает кшггур с током в маггошкш поле,

dW = р_тВ sin а 4®. Интегрлруя, находим, что

- const.

Если положить соя«4 = 0, формула приобретает вид

W = - р_тВ cos a = - pi^B. (48.6)

Для вакуума в гауссовой системе можно написать

W'.-fteH. (48.7)

11* 1«3

Отметим, что формула (48.6) аналогична выраже­нию (14.4) для энергии, которой обладает диполь в элек­трическом поле.

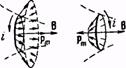
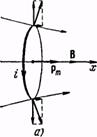
Теперь рассмотрим плоский контур с током в неод­нородном магнитном поле. Для простоты будем вначале считать контур круговым. Предположим, что поле изме­няется быстрее всего в направлении х, совпадающем с направлением В в том месте, где расположен центр контура, и что магнитный момент контура ориентирован вдоль поля (рис 91,а).

S)

Рис. 91.

Сила df, действующая на элемент контура, перпен­дикулярна к В, т. е. к линии магнитной индукции в месте пересечения ее с d\. Поэтому силы, приложенные к раз­личным элементам контура, образуют симметричный ко­нический «веер» (рис. 91,6). Их результирующая f на­правлена в сторону возрастания В и, следовательно, втя­гивает контур в область более сильного поля. Очевидно, что чем сильнее изменяется поле (чем больше градиент

дВ\ поля -aj-)i тем меньше угол раствора «веера» и тем

больше, при прочих равных условиях, результирующая сила f. Если изменить направление тока в контуре на обратное (при этом р_т станет противоположным В), на­правления всех сил df и их результирующей f изменят­ся на обратные (рис. 91,в). Следовательно, при такой взаимной ориентации векторов р_т и В контур будет вы­талкиваться из поля.

С помощью выражения (48.6) для энергии контура в магнитном поле легко найти количественное выраже­ние для I. Если ориентация магнитного момента по отно-

шению к полю остается неизменной (а = const), то W будет зависеть только от х (через В). Дифференцируя W по к и изменяя у результата знак, получим проекцию силы на ось х

_f dW дБ

По предположению в других направлениях поле из­меняется слабо, поэтому проекциями силы на другие оси можно пренебречь и считать, что f = f_x. Итак,

f = />_m-|f-cosa. (48.8)

Согласно полученной нами формуле сила, действую­щая на контур с током в неоднородном магнитном поле, зависит от ориентации магнитного момента контура от­носительно направления поля. Если векторы р_т и В сов­падают по направлению (а = 0),сила положительна, т.е.

„ (дБ направлена в сторону возрастания В 1-^ — предпола-

гается положительным; в противном случае знак и на­правление силы изменятся на противоположные, но сила по-прежнему будет втягивать контур в область сильного поля). Если р_т и В антипараллельны (а = я), сила от­рицательна, т. е. направлена в сторону убывания В. Этот результат мы уже получили качественно с по­мощью рис. 91.

Разумеется, что кроме силы (48.8) на контур с током в неоднородном магнитном поле будет действовать так­же вращательный момент (48.3).

§ 49. Работа, совершаемая при перемещении тока в магнитном поле

Допустим, что провод с током может свободно пере­мещаться во внешнем магнитном поле. Это можно осу­ществить с помощью скользящих контактов между кон­цами провода и остальными участками замкнутой цепи (рис. 92). Внешнее поле будем предполагать однород­ным и перпендикулярным к плоскости контура. При ука­занных на рисунке направлениях тока и поля сила будет направлена вправо и равна

/ = 1В1,

где / — длина перемещающегося участка тока. На пути ds эта сила совершит над проводником работу dA = fds = iBlds.

Произведение Ids равно заштрихованной площади (рис. 92), a Bids — потоку магнитной индукции d<& че­рез эту площадку. Поэтому можно написать, что

dA = id<&, (49.1)

где с?Ф — поток магнитной индукции, пересекаемый про-

водником при его движении.

Полученный нами результат легко обобщить на слу-

чай неоднородного поля. Для этого нужно разбить про-

водник на участки dl и сло­жить элементарные работы, со­вершаемые над каждым участ­ком (в пределах каждой ма­лой площадки dlds магнитную индукцию можно считать по­стоянной).

Если вектор В образует с нормалью к контуру угол а, отличный от нуля, направле-

ние силы составит с направлением перемещения также

угол a (f перпендикулярна к В) и

dA = f cos ads = iB_nl ds,

где 5_n = Bcosa — составляющая вектора В по направ­лению нормали к площадке Ids. Произведение B_nlds есть dФ — поток, пересекаемый проводником. Таким об­разом и в этом случае мы приходим к формуле (49.1). Заметим, что работа (49.1) совершается не за счет магнитного поля (как было указано в § 47, сила Лорен­ца работы над зарядами не совершает), а за счет источ­ника, поддерживающего ток в контуре¹).

') В § 56 будет показано, что при изменениях потока магнит­ной индукции, пронизывающего контур, в этом контуре возникает

с[ф э. д. с. индукции?/= -- —. Следовательно, в этом случае источ<

ник тока, кроме работы, затрачиваемой на выделение ленц-джоулева тепла, должен совершать дополнительную работу против э. д. с. индукции, определяемую выражением

которое совпадает с (49.1). 169

Найдем работу, совершаемую над замкнутым конту­ром с током при его перемещении в магнитном поле. Вна­чале предположим, что контур, перемещаясь, остается все время в одной плоскости (рис. 93; вектор В направ­лен за чертеж). Силы, приложенные к участку контура / — 2, образуют с направлением перемещения острые уг-. лы. Следовательно, совершаемая ими работа А\ положи-. тельна. Согласно формуле (49.1) эта рябота пропорцио­нальна силе тока в кон-

туре г'"и пересеченному /'

участком / — 2 потоку магнитной индукции. Уча­сток / — 2 пересекает при своем движении поток Фо через заштрихованную поверхность и поток Ф_к, пронизывающий контур в его конечном положении. Таким образом,

Силы, действующие ^Рис- ⁹³-

на участок контура 2 — /,

образуют с направлением перемещения тупые углы._: Поэтому совершаемая ими работа А₂ отрицательна, Абсолютная величина ее пропорциональна потоку, пере­секаемому участком 2 — /, который слагается из Ф₀ и Ф_н — потока, пронизывающего контур в начальном по­ложении. Следовательно,

Л₂=-/(Ф₀ + Фн). Работа, совершаемая над всем контуром, равна

Разность магнитного потока через контур в конце пе­ремещения Ф„ и потока в начале Ф_н дает приращение потока через контур ДФ. Таким образом,

(49.2)

В гауссовой системе формула для работы имеет вид

— /ДФ. с

(49.3) 167

При выводе формулы (49.2) мы сделали определен­ные предположения о характере движения контура. Можно показать, что эта формула остается справедли­вой при любом движении контура в произвольном маг­нитном поле. В частности, при повороте контура в одно­родном поле из положения, в котором векторы р_т и В направлены в противоположные стороны, в положение, при котором эти векторы совпадают по направлению, силы поля совершают над контуром работу

А = 21SB

(ф_н = — BS, вектор В и положительная нормаль имеют противоположные направления, вследствие чего Ф_н от­рицателен; Ф_к = 55). Учитывая, что iS = р_т — магнит­ному моменту контура, получаем

Тот же результат получается с помощью выражения (48.6) для энергии контура в магнитном поле:

А = W_n - W_K - р_тВ - (- _РтВ) - 2р_тВ.

Дата добавления: 2015-06-27