Внезапное расширение трубопровода

Примеры расчета местных сопротивлений

Мы уже заметили, что местные сопротивления зависят от конкретной формы и конфигурации элементов трубопровода, в которых происходят изменение скорости течения жидкости, отрыв потока от стенок русла, возникновение вихреобразования. В общем случае коэффициенты потерь определяют опытным путем, учитывая то, что при турбулентном режиме течения эти коэффициенты определяются в основном формой местных сопротивлений и очень мало зависят от изменения абсолютных размеров русла, скорости потока и вязкости жидкости, т. е. от числа Re.

Для некоторых простейших местных сопротивлений, таких как расширения, сужения и повороты русла (как внезапные, так и постепенные), выражения для коэффициентов потерь могут быть рассчитаны теоретически.

При внезапном расширении трубопровода (или русла канала) поток срывается с угла и расширяется не внезапно, как сама труба, а постепенно, причем в кольцевом пространстве между потоком и стенкой образуются вихри, которые и являются причиной потерь энергии, т. е. возникновения сопротивления (рис. 5.5).

Выделим в потоке, движущемся по трубопроводу с внезапным расширением, два сечения (рис. 5.5):

· сечение 1 – 1 – в месте внезапного расширения;

· сечение 2 – 2 – на некотором удалении от места внезапного расширения.

Рис. 5.5

Обозначим параметры в сечении 1 – 1 индексом «1»: ω ₁– площадь сечения трубы; 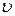₁ – скорость течения жидкости; p ₁ – давление.

Соответствующие параметры в сечении 2 – 2 (ω ₂, 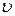₂, p ₂) – индексом «2».

Сделаем следующие исходные предположения:

1. Потери на трение на участке расширения трубы между сечениями 1 – 1 и 2 – 2 незначительны, ими можно пренебречь.

2. Давление в сечении 1 – 1 действует по всему сечению ω ₂, так как хотя труба и расширилась, но параметры (скорость и давление) измениться еще не успели.

Воспользуемся теоремой механики (теоремой Эйлера) о том, что изменение количества движения системы материальных точек в проекции на ось движения равно импульсу действующих сил (импульс тела равен импульсу силы), т. е. .

Из рис. 5.5 видно, что жидкость, занимавшая в начальный момент времени суммарный объем отсеков I и III, через промежуток времени δt переместится и займет объем отсеков II и III. Очевидно, что изменение количества движения произойдет только за счет разницы его в отсеках II и I, так как отсек III является общим для обоих моментов времени и за время δt количество движения жидкости в нем не изменится.

Тогда имеем

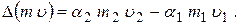
Здесь – коэффициенты количества движения, учитывающие неравномерность распределения скоростей в сечениях 1 – 1 и 2 – 2. Поскольку мы рассматриваем случай развитого турбулентного движения в трубе (тем более с учетом угловых завихрений), то, как условились при выводе уравнения Бернулли для реальной жидкости, для турбулентного движения можно принять 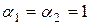. Учтем также, что

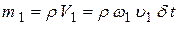
и соответственно

.

Тогда:

.

При расчете импульса сил, действующих на выделенный объем жидкости (между сечениями 1 – 1 и 2 – 2), проекции на ось движения будут иметь только силы продольного давления, потому что силы тяжести и силы давления на боковую поверхность трубы перпендикулярны оси движения жидкости и проекции на нее не дают.

Тогда импульс сил будет

.

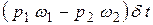Вспомним наше второе исходное предположение о том, что давление p ₁ действует по всему сечению ω ₂, тогда для импульса сил можно записать

.

Таким образом, у нас получится уравнение

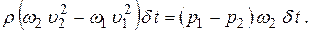
Заменим в этом уравнении (из условия сохранения массы)

и получим:

Разделим обе части этого равенства на :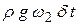

(5.5)

Составим теперь уравнение Бернулли для сечений 1 – 1 и 2 – 2, с учетом того, что 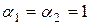и геометрическая высота центра тяжести сечения отсчитывается от оси движения, т. е. 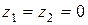. Тогда

.

Выразим отсюда потери напора h _пот:

.

Последний член этого уравнения заменим, используя формулу (5.5):

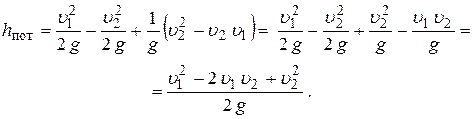
Применяя в числителе формулу сокращенного умножения, окончательно получим:

.

(5.6)

Полученное можно сформулировать так: потеря напора при внезапном расширении русла (трубопровода) равна напору, определенному по разности скоростей (или напору потерянной скорости).

Это положение называют теоремой Борда, а формулу (5.6) называют формулой Борда-Карно.

Приведем формулу (5.6) к общему виду формулы для гидравлических сопротивлений, т. е. к виду – :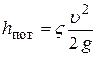

а) оставим в формуле (5.6) только скорость 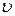₂:

,

видим, что в этом случае коэффициент сопротивления будет:

;

(5.7)

б) выразим коэффициент сопротивления через скорость 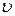₁:

,

в этом случае коэффициент сопротивления будет

.

(5.8)

Эти зависимости хорошо подтверждаются опытом и широко используются в расчетах.

Для частного случая, когда площадь ω ₂ существенно больше площади ω ₁, т. е. когда жидкость по трубе подводится к очень большому резервуару, из формулы (5.8) имеем 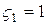и , т. е. в этом случае теряется весь скоростной напор (вся кинетическая энергия, которой обладает движущаяся жидкость).

Потеря напора при внезапном расширении расходуется исключительно на вихреобразование, связанное с отрывом потока от стенок.

Дата добавления: 2015-06-28