Сортировка выбором

Сортировка вставкой

Принцип метода:

Массив разделяется на две части: отсортированную и неотсортированную. Элементы из неотсортированной части поочередно выбираются и вставляются в отсортированную часть так, чтобы не нарушить в ней упорядоченность элементов. В начале работы алгоритма в качестве отсортированной части массива принимают только один первый элемент, а в качестве неотсортированной части – все остальные элементы

Таким образом, алгоритм будет состоять из n-1-го прохода (n – размерность массива), каждый из которых будет включать четыре действия:

- взятие очередного i-го неотсортированного элемента и сохранение его в дополнительной переменной,

- поиск позиции j в отсортированной части массива, в которой присутствие взятого элемента не нарушит упорядоченности элементов;

- сдвиг элементов массива от i-1-гo до j-го вправо, чтобы освободить найденную позицию вставки;

- вставка взятого элемента в найденную j-ю позицию.

Для реализации данного метода можно предложить несколько алгоритмов, которые будут отличаться способом поиска позиции вставки. Наиболее оптимальным является алгоритм, объединяющий в одном цикле поиск позиции вставки и сдвиг элементов.

Принцип метода:

Находим (выбираем) в массиве элемент с минимальным значением на интервале от 1-го элемента, до n-го (последнего) элемента и меняем его местами с первым элементом. На втором шаге находим элемент с минимальным значением на интервале от 2-го до n-го элемента и меняем его местами со вторым элементом.

И так далее для всех элементов до n-1-го.

Сортировка обменом ("пузырьковая" сортировка)

Принцип метода:

Слева направо поочередно сравниваются два соседних элемента, и если их взаиморасположение не соответствует заданному условию упорядоченности, то они меняются местами. Далее берутся два следующих соседних элемента и так далее до конца массива.

После одного такого прохода на последней n-ой позиции массива будет стоять максимальный элемент ("всплыл" первый "пузырек") Поскольку максимальный элемент уже стоит на своей последней позиции, то второй проход обменов выполняется до n-1-ro элемента. И так далее. Всего требуется n-1 проход.

Варианты заданий к лабораторной работе №5

1. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем сумму ее положительных четных элементов. Переставляя строки заданной матрицы, расположить их в соответствии с ростом характеристик. Использовать сортировку обменами.

2. Сортировка простыми вставками. Дана действительная матрица размера п ´ m (). Упорядoчить (переставить) элементы 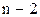строки матрицы по неубыванию значений.

3. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем сумму ее отрицательных четных элементов. Переставляя строки заданной матрицы, расположитьих в соответствии с неубыванием характеристик. Использовать сортировку выбором.

4. Сортировка обменами. Дана действительная матрица размера п ´ m (). Упорядoчить (переставить) элементы 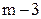столбца матрицы по невозрастанию значений.

5. Дана целочисленная прямоугольная матрица. Характеристикой столбца целочисленной матрицы назовем сумму модулей его отрицательных нечетных элементов. Переставляя столбцы заданной матрицы, расположитьих в соответствии с ростом характеристик. Использовать сортировку простыми вставками.

6. Сортировка обменами. Дана действительная матрица размера п ´ m. Упорядoчить (переставить) строки матрицы по неубыванию значений последних элементов строк.

7. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем модуль суммы ее отрицательных элементов. Переставляя строки заданной матрицы, расположитьих в соответствии с невозрастанием характеристик. Использовать сортировку выбором.

8. Сортировка обменами. Дана действительная матрица размера п ´ m. Упорядoчить (переставить) строки матрицы по невозрастанию значений первых элементов столбцов.

9. Сортировка простыми вставками. Дана действительная матрица размера п ´ m. Упорядoчить (переставить) строки матрицы по невозрастанию сумм элементов строк.

10. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем среднее арифметическое значение ее элементов. Переставляя строки заданной матрицы, расположитьих в соответствии с убыванием характеристик. Использовать сортировку выбором.

11. Сортировка обменами. Дана действительная матрица размера п ´ m. Упорядoчить (переставить) строки матрицы по неубыванию значений наименьших элементов строк.

12. Сортировка простыми вставками. Дана действительная матрица размера п ´ m. Упорядoчить (переставить) строки матрицы по невозрастанию значений наибольших элементов строк.

13. Сортировка обменами. Дана действительная матрица размера п ´ m. Упорядoчить (переставить) строки матрицы по неубыванию значений разности максимальных минимальных элементов строк.

Варианты заданий к лабораторной работе №5 (иностранные студенты)

1. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем сумму ее положительных четных элементов. Составить одномерный массив характеристик.

2. Дана действительная матрица размера п ´ m ().Составить одномерный массив характеристик - элементов 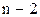строки матрицы.

3. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем сумму ее отрицательных четных элементов. Составить одномерный массив характеристик.

4. Дана действительная матрица размера п ´ m ().Составить одномерный массив характеристик - элементы 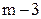столбца матрицы.

5. Дана целочисленная прямоугольная матрица. Характеристикой столбца целочисленной матрицы назовем сумму модулей его отрицательных нечетных элементов. Составить одномерный массив характеристик.

6. Дана действительная матрица размера п ´ m. Составить одномерный массив характеристик - значений последних элементов строк.

7. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем модуль суммы ее отрицательных элементов. Составить одномерный массив характеристик.

8. Дана действительная матрица размера п ´ m. Составить одномерный массив характеристик - значений первых элементов столбцов.

9. Дана действительная матрица размера п ´ m. Составить одномерный массив характеристик - сумм элементов строк.

10. Дана целочисленная прямоугольная матрица. Характеристикой строки целочисленной матрицы назовем среднее арифметическое значение ее элементов. Составить одномерный массив характеристик.

11. Дана действительная матрица размера п ´ m. Составить одномерный массив характеристик - значений наименьших элементов строк.

12. Дана действительная матрица размера п ´ m. Составить одномерный массив характеристик - значений наибольших элементов строк.

13. Дана действительная матрица размера п ´ m. Составить одномерный массив характеристик - значений разности максимальных минимальных элементов строк.

Дата добавления: 2015-06-28