Определение истинной величины расстояний

Общие сведения о метрических задачах

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Какие задачи называются позиционными?

2. Какова последовательность решения задач на пересечение на комплексном чертеже?

3. Какая прямая является линией пересечения плоскости общего положения с горизонтальной плоскостью уровня?

4. Какая прямая является линией пересечения плоскости общего положения с фронтально проецирующей плоскостью?

5. По какой линии пересекаются две фронтально проецирующие плоскости?

6. Как определяется видимость при пересечении двух плоскостей общего положения?

7. Как строится линия пересечения поверхностей плоскостью?

8. Какие линии могут быть получены в сечении прямого кругового цилиндра, конуса, сферы?

9. Что такое линия среза?

10. Что представляет собой вырез?

11. Чем можно задать необходимую форму выреза?

12. Как строят линию пересечения двух поверхностей?

13. Какие вспомогательные поверхности удобно использовать при построении точек линии пересечения двух поверхностей?

14. В чем сущность способа вспомогательных секущих плоскостей в построении линии пересечения двух поверхностей?

15. По каким линиям пересекаются соосные поверхности вращения?

16. Когда можно использовать вспомогательные сферы при построении линии пересечения двух поверхностей?

17. По каким линиям пересекаются два прямых круговых цилиндра одного диаметра, если их оси пересекаются? Почему?

18. Какую линию называют линией перехода и как она вычеркивается при изображении пересекающихся поверхностей?

Глава 11. МЕТРИЧЕСКИЕ ЗАДАЧИ

К метрическим относятся задачи, связанные с определением истинных (натуральных) величин расстояний, углов и плоских фигур на комплексном чертеже. Можно выделить три группы метрических задач.

1. Группа задач, включающих в себя определение расстояний от точки до другой точки; от точки до прямой; от точки до плоскости; от точки до поверхности; от прямой до другой прямой; от прямой до плоскости; от плоскости до плоскости. Причем расстояние от прямой до плоскости и между плоскостями измеряется в тех случаях, когда они параллельны.

2. Группа задач, включающая определение углов между пересекающимися или скрещивающимися прямыми, между прямой и плоскостью, между плоскостями (имеется в виду определение величины двухгранного угла).

3. Группа задач, связанная с определением истинной величины плоской фигуры и части поверхности (развертки).

Приведенные задачи могут быть решены с применением различных способов преобразования чертежа. В основе решения метрических задач лежит свойство прямоугольного проецирования, заключающееся в том, что любая геометрическая фигура на плоскость проекций проецируется в натуральную величину, если она лежит в плоскости, параллельной этой плоскости проекций. Решение задач значительно упрощается, если хотя бы одна из геометрических фигур, участвующих в задачах, занимает частное положение. Если одна из геометрических фигур не занимает частного положения, необходимо выполнить определенные построения, позволяющие провести одну из них в это положение.

Некоторые задачи на определение расстояний рассматривались в предыдущих разделах. Например, в § 42 определялась натуральная величина отрезка прямой линии методом треугольника, в § 57 определялась натуральная величина отрезка способом плоскопараллельного переноса. Эта задача может быть также решена способом замены плоскостей проекций (см. § 58) или способом вращения (см. § 59). Определение длины отрезка прямой позволяет решить задачу определения расстояния от точки до точки, так как это расстояние и определяется отрезком прямой. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой. Отрезок этого перпендикуляра изображается в натуральную величину на плоскости в том случае, если он проведен к проецирующей прямой. Значит, нужно преобразовать чертеж данной прямой, сделав ее в новой системе плоскостей проекций проецирующей (см. § 58, задача 2). На рис. 140 определено расстояние от точки М до прямой АВ:

1) П2_|_П1-> П1_|_П4, П4 ||АВ, П1/П4 ||A1B1;

2) П1П4 -> П4_|_П5, П5 _|_AB, П4/П5 _|_A4B4;

3) M5K5 — истинное расстояние от точки М до прямой AB;

4) чтобы построить проекции перпендикуляра МК в исходной системе плоскостей, строят основание перпендикуляра— точку К—на прямой АВ из условия, что в системе П4 _|_П5; он занимает положение линии уровня, т. е.

M4K4_|_A4B4. Горизонтальная и фронтальная проекции точки К определяются по линиям из условия принадлежности ее прямой АВ. Расстояние от точки до плоскости измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Так как перпендикуляр к проецирующей плоскости есть линия уровня, то удобно иметь на чертеже «вырожденную» проекцию данной плоскости, т. е. преобразовать чертеж (см. § 58, задача 3). На рис. 141 построены проекции перпендикуляра МК, отрезок которого определяет расстояние от точки М до плоскости Ө(ABC):

Рис. 140

1) П1,П2→П1_|_П4, П4_|_Ө, П1 /П4 _|_ h ₁(A, 1)€ 0;

2) М4K4 _|_Ө4 — истинная величина расстояний от точки М до плоскости Ө;

3)M1K1_|_K4Kl или || П1/ П4;

4) K2 построена с помощью высоты точки К, измеренной на плоскости П4.

Расстояние между параллельными прямыми измеряется отрезком перпендикуляра между ними. На рис. 142 определено расстояние между прямыми а и b путем преобразования чертежа прямых. Сначала построено

Рис. 141

изображение прямых на плоскости П4_|_П1. В этой системе плоскостей прямые занимают положение линии уровня:

а(b)|| П4; П1 /П4 ||а,(b₁).

В системе плоскостей П4 _|_ П5 прямые занимают проецирующее по отношению к плоскости П5 положение:

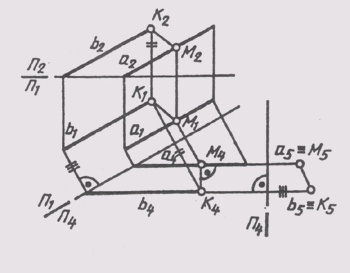
Рис. 142

П5 _|_ а(b); П4/П5 _|_a4(b4) Отрезок M5K5 между вырожденными проекциями прямых определяет истинную величину расстояния между прямыми а и Ъ. Построения проекций перпендикуляра МК в исходной системе плоскостей проекций аналогичны рассмотренным ранее.

Для определения расстояния между скрещивающимися прямыми необходимо одну из прямых сделать проецирующей в новой системе плоскостей проекций.

Расстояние от прямой до плоскости, параллельной прямой, измеряется отрезком перпендикуляра, опущенного из любой точки прямой на плоскость. Значит, достаточно плоскость общего положения преобразовать в положение проецирующей плоскости, взять на прямой точку, и решение задачи будет сведено к определению расстояния от точки до плоскости.

Расстояние между параллельными плоскостями измеряется отрезком перпендикуляра между ними, который легко строится, если плоскости займут проецирующее положение в новой системе плоскостей проекции, т. е. опять используется третья исходная задача преобразования чертежа.

§ 70. Определение истинной величины углов

Задачу на определение истинной величины углов (плоских) удобнее решать путем преобразования исходного чертежа способом вращения вокруг линии уровня. Истинная величина углов между пересекающимися прямыми с и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f (1, 2) до совмещения ее с фронтальной плоскостью уровня Ф (Ф1), проходящей через

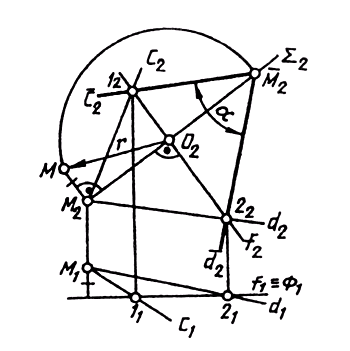
Рис. 143

фронталь f Проекция MI совмещения вершины М угла между прямыми с и d находится на проекции Σ2 фронтально проецирующей плоскости Σ, в которой вращается точка М. Определив с помощью прямоугольного треугольника О2М2М натуральную величину радиуса вращения r и отложив ее на проекции Σ2 от фронтальной проекции центра вращения, получаем изображение точки М на плоскости П2 в совмещенном с плоскостью Ф положении. Соединяя фронтальные проекции неподвижных точек 1 и 2 с построенной точкой М, получаем проекции с2 и d2, совмещенных с плоскостью Ф прямых с и d. Угол между прямыми с2 и d2 определяет натуральную величину искомого угла между пересекающимися прямыми с и d.

Эта задача также может быть решена способом замены плоскостей проекций. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем — четвертую.

Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым.

Угол а между прямой l и плоскостью Ө может быть определен через дополнительный угол β между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 144). Угол β дополняет искомый угол а до 90°. Определив истинную величину угла β путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром и, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла α между прямой l и плоскостью Ө.

Истинная величина двугранного угла — между двумя плоскостями Ө и λ. — может быть определена или путем замены плоскости проекций с целью преобразования ребра двугранного угла в проецирующую прямую (задачи 1 и 2), или если ребро не задано, как угол между двумя перпендикулярами n¹ и n², проведенными к данным плоскостям (см. § 61) из произвольной точки М пространства (см. рис. 145). В плоскости этих перпендикуляров при точке М получаем два плоских

Рис. 144

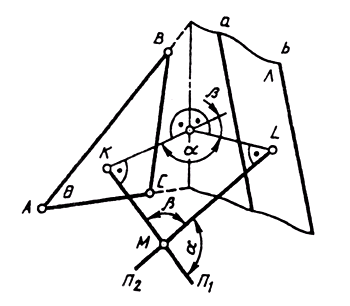
Рис. 145

угла α и β, которые соответственно равны линейным углам двух смежных углов (двугранных), образованных плоскостями Ө и λ,. Определив истинную величину углов между перпендикулярными n¹ и n² путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями Ө и λ.

Дата добавления: 2015-06-28