Расчетно-графическая работа №2

Векторная алгебра и аналитическая геометрия

(1 курс, 1 семестр, дневное отделение)

Вариант №____

Выполнил студент группы______

_____________________________

Фамилия И.О.

Проверил ассистент:

_____________________________

Фамилия И.О.

Ишимбай 2012

1. На плоскости относительно некоторого базиса даны координаты трех векторов:

при N – четном: ;

при N – нечетном: .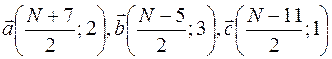

1) Найти координаты векторов ; .

2) Проверить, что векторы и образуют базис на плоскости. Найти координаты вектора 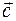в этом базисе.

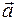3) Определить, при каком значении параметра векторы и 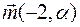будут коллинеарными.

4) Найти координаты вектора .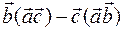

5) Вычислить .

6) Найти косинус угла между векторами и .

2. В пространстве относительно некоторого базиса даны координаты трех векторов:

при N – четном: ;

при N – нечетном:

.

1) Найти координаты вектора .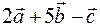

2) Найти координаты вектора .

3) Вычислить .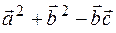

4) Найти косинус угла между векторами и .

5) Найти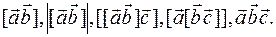

3. На плоскости относительно декартовой системы координат даны координаты трех точек:

при N – четном: ;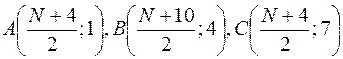

при N – нечетном: .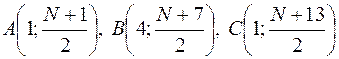

Найти:

1) координаты вектора ;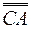

2) координаты точек M₁, M₂, M₃, делящих отрезки 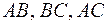в отношениях 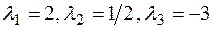, соответственно;

3) координаты центра тяжести треугольника ABC;

4) длину отрезка AB;

5) площадь треугольника ABC;

6) угол B.

4. Относительно декартовой системы координат даны координаты вершин треугольника:

при N – четном: ;

при N – нечетном: .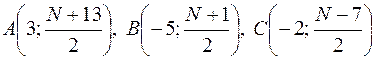

Составить уравнения:

1) трех его сторон;

2) медианы, проведенной из вершины С;

3) высоты, опущенной из вершины А на сторону ВС.

5. Относительно декартовой системы координат даны координаты точки:

при N – четном: ;

при N – нечетном: .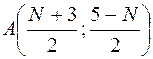

Найти:

1) угловой коэффициент прямой , проходящей через точку А параллельно вектору ;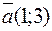

2) уравнение прямой , проходящей через точку А под прямым углом к прямой ;

3) уравнение прямой 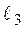, проходящей через точку А и отсекающей на осях координат равные отрезки;

4) косинус угла между прямыми и ;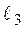

5) уравнения прямых 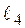и 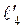, проходящих через начало координат параллельно прямой ;

6) расстояние между прямыми и ;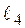

7) координаты точки В пересечения прямых 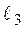и ;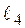

8) расстояние от точки В до прямой .

6. Даны четыре точки , , , 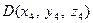. Составить уравнения:

1) Плоскости ABC

2) Прямой AB

3) Прямой DM перпендикулярной к плоскости ABC

4) Прямой CN параллельно прямой AB

5) Плоскости, проходящей через точку D перпендикулярно к прямой AB

6) Плоскости, проходящей через точку D параллельно прямым АВ и АС

Найти:

7. точку , симметричную точке D относительно прямой AB

8. точку , симметричную точке D относительно плоскости ABC

9. Синус угла между прямой AD и плоскостью ABC

10. Косинус угла между координатной плоскостью Oxy и плоскостью ABC

1. A(3, 1, 4), B(-1, 6, 1), C(-1, 1, 6), D(0, 4, -1).

2. A(3, -1, 2), B(-1, 0, 1), C(1, 7, 3), D(8, 5, 8).

3. A(3, 5, 4), B(5, 8, 3), C(1, 2, -2), D(-1, 0, 2).

4. A(2, 4, 3), B(1, 1, 5), C(4, 9, 3), D(3, 6, 7).

5. A(9, 5, 5), B(-3, 7, 1), C(5, 7, 8), D(6, 9, 2).

6. A (0,7,1), B (2,-1,5), C (1,6,3), D (3,-9,8).

7. A(5,5,4), B (1,-1,4), C (3,5,1), D (5,8,-1).

8. A (6,1,1), B (4,6,6), C (4,2,0), D (1,2,6).

9. A (7,5,3), B (9,4,4), C (4,5,7), D (7,9,6).

10. A (6,8,2), B (5,4,7), C (2,4,7), D(7, 3, 7).

11. A (4,2,5), B (0,7,1), C (0,2,7), D(1,5,0).

12. A (4,4,10), B (7,10,2), C (2,8,4), D(9,6,9).

13. A (4,6,5), B (6,9,4), C (2,10,10), D(7, 5,9).

14. A (3,5,4), B (8,7,4), C (5,10,4), D(4,7,8).

15. A (10,9,6), B (2,8,2), C (9,8,9), D(7, 10,3).

16. A (1,8,2), B (5,2,6), C (5,7,4), D(4,10,9).

17. A (6,6,5), B (4,9,5), C (4,6,11), D(6,9,3).

18. A (7,2,2), B (-5,7,-7), C (5,-3,1), D(2,3,7).

19. A (8,-6,4), B (10, 5, -5), C (5,6,-8), D(8,10,7).

20. A (1,-1,3), B (6,5,8), C (3,5,8), D(8,4,1).

7. Найти угол между плоскостями

1) x-3y+5=0, 2x-y+5z-16=0.

2) x-3y+z-1=0, x+z-1=0.

3) 4x-5y+3z-1=0, x-4y-z+9=0.

4) 3x-y+2z+15=0, 5x+9y-3z-1=0.

5) 6x+2y-4z+17=0, 9x+3y-6z-4=0.

6) x-y +z-1=0, x+y -z+3=0.

7) 3y-z=0, 2y+z=0.

8) 6x+3y-2z=0, x+2y+6z-12=0.

9) x+2y+2z-3=0, 16x+12y-15z-1=0.

10) 2x-y+5z+16=0, x+2y+3z+8=0.

11) 2x+2y+z-1=0, x+z-1=0.

12) 3x+y+z-4=0, y+z+5=0.

13) 3x-2y-2z-16=0, x+y-3z-7=0.

14) 2x+2y+z+9=0, x-y+3z-1=0.

15) x+2y+2z-3=0, 2x-y+z+5=0.

16) 3x+2y-3z-1=0, x+y+z-7=0.

17) x-3y-2z-8=0, x+y-z+3=0.

18) 3x-2y+3z+23=0, y+z+5=0.

19) x+y+3z-7=0, y+z-1=0.

20) x-2y+2z+17=0, x-2y-1=0.

8. Написать каноническое и параметрические уравнения прямой заданной пересечением плоскостей

1) 2x+y+z-2=0, 2x-y-z+6=0.

2) x–3y+2z+2=0, x+3y+z+14=0.

3) x–2y+z-4=0, 2x+2y-z-8=0.

4) x+y+z-2=0, x-y-2z+2=0.

5) x+5y+2z+11=0, x-3y-2z+3=0.

6) 3x+y-z-6=0, 3x-y+2z=0.

7) x+5y+2z+11=0, x-y-z-1=0.

8) 3x+4y-2z+1=0, 2x-4y+3z+4=0.

9) 5x+y-3z+4=0, x-y+2z+2=0.

10) x-y-z-2=0, x-2y+z+4=0.

11) 4x+y-3z+2=0, 2x-y+z-8=0.

12) 3x+3y-2z-1=0, 2x-3y+z+6=0.

13) 6x-7y-4z-2=0, x+7y-z-5=0.

14) 8x-y-3z-1=0, x+y+z+10=0.

15) 6x-5y-4z+8=0, 6x+5y+3z+4=0.

16) x+5y-z-5=0, 2x-5y+2z+5=0.

17) 2x-3y+z+6=0, x-3y-2z+3=0.

18) 5x+y+2z+4=0, x-y-3z+2=0.

19) 4x+y+z+2=0 2x-y-3z-8=0.

20) 2x+y-3z-2=0, 2x-y+z+6=0.

9. В данной системе координат эллипс имеет каноническое уравнение. Составить это уравнение, зная, что расстояние между фокусами равно 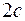, большая полуось равна :

при N – четном: ;

при N – нечетном: .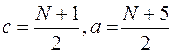

Найти:

1) эксцентриситет эллипса;

2) уравнения директрис;

3) расстояние от правого фокуса до ближайшей директрисы.

10. В данной системе координат гипербола имеет каноническое уравнение. Составить это уравнение, зная, что расстояние между фокусами равно 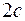, большая полуось равна :

при N - четном: ;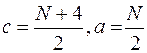

при N – нечетном: .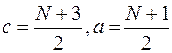

Найти:

1) эксцентриситет гиперболы;

2) уравнения директрис;

3) уравнения асимптот;

4) длину отрезка асимптоты гиперболы, заключенного между ее центром и директрисой;

5) расстояния от фокусов гиперболы до ее асимптот.

11. В данной системе координат парабола имеет каноническое уравнение. Составить это уравнение, зная, что расстояние от фокуса до директрисы равно N.

при N - четном: осью симметрии является ось Ох;

при N – нечетном: осью симметрии является ось Оу.

Найти:

1) координаты фокуса;

2) уравнение директрисы;

3) координаты точек пересечения параболы с окружностью

12. Построить тело, ограниченное указанными поверхностями.

1. а)

б) .

2. а)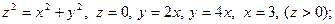

б) .

3. а)

б) .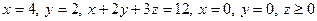

4. а)

б) .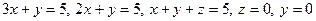

5. а)

б)

6. а)

б)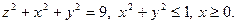

7. а)

б)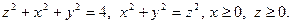

8. а)

б)

9. а)

б)

10. а) ;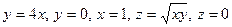

б)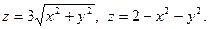

11. а)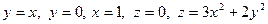

б)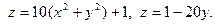

12. а) ;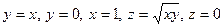

б)

13. а)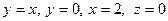

б)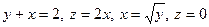

14. а)

б)

15. а)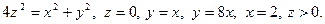

б)

16. а)

б)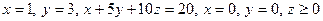

17. а)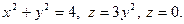

б)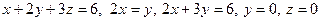

18. а)

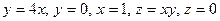
б)

19. а)

б)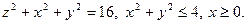

20. а)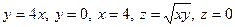

б)

Дата добавления: 2015-06-28