Простейшая модель размера партии при отсутствии дефицита

Библиографический список

1. Федосеев В.В. Экономико-математические модели и методы в маркетинге, 1998.

Предположим,что некоторой фирме для нормального функционирования в течении года требуется ресурсы в объеме единиц (для предприятий торговли этот запас определяет величину сбыта за некоторый промежуток времени). Интенсивность сбыта величина постоянная , т.е. спрос известен заранее. Выполнение заказа осуществляется мгновенно, т.е. время доставки равно нулю.

Работа фирмы может происходить по следующей схеме. К началу производственного периода создается запас из единиц товара, который с течением времени уменьшается с интенсивностью и достигает нуля в момент окончания производственного процесса , т.е. . В этом случае годовой спрос фирмы удовлетворяется за счет одного заказа. В другом случае к началу производственного процесса запасается единиц товара. Этот запас израсходуется к середине периода и для продолжения производственного процесса должно произойти пополнение запаса на величину путем заказа товара. В общем случае пополнение запаса может происходить 3,4,5 и т.д. раз за плановый промежуток. Диаграмма изменения уровня товаров на складе показана на рис.2.

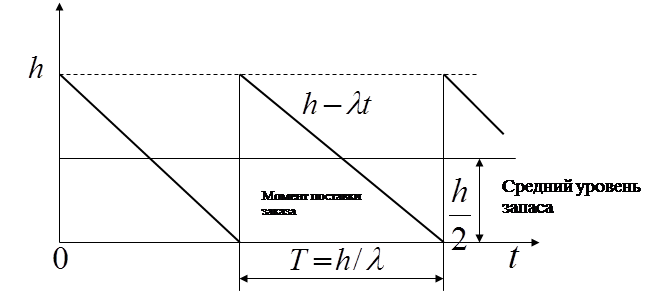Ри с. 2

С течением времени уровень запасов уменьшается равномерно до нуля. В этот момент времени поступает заказ, размер которого равен 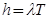, и уровень запасов восстанавливается до исходного мгновенно. Через обозначим интервал между двумя заказами, который не превышает горизонта планирования . Определим средний уровень запасов на складе, который определяет затраты на хранение. Поскольку изменение уровня запасов периодический процесс , то

.

В розничной торговле возникают определенные издержки при закупке и хранении товарных запасов, а в промышленности – издержки, связанные с производством и хранением запасов готовой продукции. В первой модели будем рассматривать лишь два вида потерь:

Потери при выполнении заказа, представляющие собой накладные расходы. Если 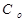- затраты на выполнение заказа, а 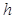- размер заказываемой партии, то издержки выполнения заказа в расчете на единицу товара составляют при увеличении размера партии они уменьшаются. Для определения потерь за календарный период(год) полученную величину нужно умножить на потребное количество товара . Но - число заказов, тогда

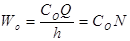. (1)

Издержки хранения запасов обычно выражают упущенную выгоду от вложения капитала в запасы ,

где 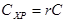выражается в процентах от закупочной цены товара, 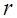- ставка процента, 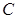- цена единицы товара, - средний уровень запасов на складе. Тогда затраты хранения равны

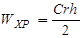. (2)

Общие годовые затраты создания и управления запасами включают в себя расходы (1), (2)

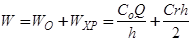. (3)

Графики функций (1) – (3) показаны на рис.3, где видно, что функция совокупных затрат 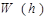имеет экстремум в т. . Это обстоятельство наталкивает на мысль найти оптимальный размер заказа, минимизирующий затраты (3), т.е. решить задачу одномерной оптимизации

Рис.3

. (4)

Возьмем первую производную (3) по 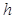и приравняем нулю

. (5)

Вычислим вторую производную

(6)

которая оказывается больше нуля. Следовательно, достаточные условия минимума функции 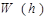выполняются и точка является решением задачи(4).Формула (5), определяющая наиболее экономичный размер заказа, называется формулой Уилсона.

Запишем формулу (5) по другому. Введем в рассмотрение число возможных заказов на пополнение . Тогда формулы (1)- (3) принимают вид:

Оптимальным числом заказов будем считать N*, минимизирующее затраты

. (7)

В результате получаем

. (8)

При использовании оптимальной стратегии управления(5), (8) средний уровень запасов в системе будет равен

. (9)

Средний уровень запаса в системе (а также ) пропорционален корню квадратному от стоимости заказа и годового сбыта и обратно пропорционален от стоимости товара. Поэтому средний уровень запаса более дорогих изделий ниже дешевых. Это означает, что при управлении запасами следует дифференцированно подходить к товарам различной стоимости.

Дата добавления: 2015-06-28