Графическая работа №2. Проекционное черчение

а) Построение третьего вида по двум заданным.

Содержание задания.

Построить третий вид детали по двум данным, проставить размеры, выполнить наглядное изображение детали в аксонометрической проекции. Задание взять из таблицы 6. Образец выполнения задания (рис. 5.19).

Графическую работу выполнить на листе чертежной бумаги формата А3.

Методические указания.

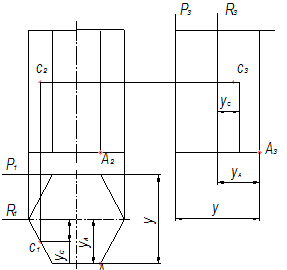
1. Выполнение чертежа начинают с построения осей симметрии видов. Расстояние между видами, а также расстояние между видами и рамкой чертежа принимают: 30-40 мм. Строят главный вид и вид сверху, Два построенных вида используют для вычерчивания третьего вида – вида слева. Этот вид чертится по правилам построения третьих проекций точек, для которых две другие проекции заданы (см. рис. 5.4 точка А). При проецировании детали сложной формы приходится одновременно вести построение всех трех изображений. При построении третьего вида в данном задании, как и в последующих, можно не наносить оси проекций, а воспользоваться «безосной» системой проецирования. За координатную плоскость можно принять одну из граней (рис. 5.5, плоскость Р), от которой отсчитываются координаты. Например, измерив отрезок на горизонтальной проекции для точки А, выражающий координату Y, переносим его на профильную проекцию, получаем профильную проекцию А₃. В качестве координатной плоскости можно взять также плоскость R симметрии, следы которой совпадают с осевой линией горизонтальной и профильной проекции, и от нее вести отсчет координат Y_С, Y_А, как показано на рис. 5.5, для точек А и С.

Рис. 5.4 Рис. 5.5

2. Каждую деталь, как бы сложна она ни была, всегда можно разбить на ряд геометрических тел: призму, пирамиду, цилиндр, конус, сферу и т.д. Проецирование детали сводится к проецированию этих геометрических тел.

3. Размеры предметов нужно наносить только после построения вида слева, так как во многих случаях именно на этом виде бывает целесообразно нанести часть размеров.

4. Для наглядного изображения изделий или их составных частей в технике применяют аксонометрические проекции. Рекомендуется предварительно изучить в курсе начертательной геометрии главу «Аксонометрические проекции».

Для прямоугольной аксонометрической проекции сумма квадратов коэффициентов (показателей) искажения равна 2, т.е.

k² + m² + n² =2,

где k, m, n –коэффициенты (показатели) искажения по осям. В изометрической

проекции все три коэффициента искажений равны между собой, т.е.

k = m = n = 0,82

Практически для простоты построений изометрической проекции коэффициент (показатель) искажения, равный 0,82, заменяют приведенным коэффициентом искажения, равным 1, т.е. строят изображение предмета, увеличенное в 1/ 0,82 = 1.22 раза. Оси X, Y, Z в изометрической проекции составляют между собой углы 120°, при этом ось Z направляют перпендикулярно к горизонтальной линии (Рис. 5.6).

В диметрической проекции два коэффициента искажения равны между собой, а третий в частном случае принимается равным 1/2 из них, т.е.,

k = n = 0,94; а m =1/2 k = 0,47

Практически для простоты построений диметрической проекции коэффициенты (показатели) искажения, равные 0,94 и 0,47, заменяют приведенными коэффициентом искажения, равным 1 и 0,5, т.е. строят изображение предмета, увеличенное в 1/ 0,94 = 1.06 раза. Ось Z в прямоугольной диметрии направлена перпендикулярно к горизонтальной линии, ось Х – под углом 7°10', ось Y – под углом 41°25'. Так как tg 7°10' ≈ 1/8, а tg 41°25' ≈ 7/8, то строить эти углы можно без транспортира, как показано на Рис. 5.7. В прямоугольной диметрии по осям Х и Z откладывают натуральные размеры, а по оси Y с коэффициентом сокращения 0,5.

Аксонометрическая проекция окружности в общем случае есть эллипс. Если окружность лежит в плоскости, параллельной одной из плоскостей проекций, то малая ось эллипса всегда параллельна аксонометрической прямоугольной проекции той оси, которая перпендикулярна к плоскости изображаемой окружности, большая же ось эллипса всегда перпендикулярна малой.

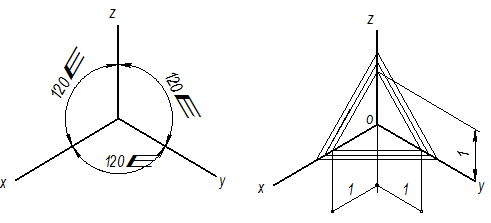
Рис. 5.6

Рис. 5.7

В данном задании наглядное изображение детали рекомендуется выполнить в изометрической проекции.

б) Простые разрезы.

Содержание задания.

Построить третий вид детали по двум данным, выполнить простые разрезы (горизонтальной и вертикальными плоскостями), проставить размеры, выполнить наглядное изображение детали в аксонометрической проекции с вырезом 1/4 части. Задание взять из таблицы 7. Образец выполнения задания (рис. 5.20).

Графическую работу выполнить на листе чертежной бумаги формата А3.

Методические указания.

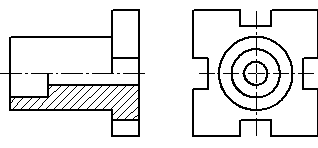
1. При выполнении задания, обратите внимание на то, что, если деталь симметрична, то необходимо в одном изображении соединить половину вида и половину разреза. При этом на виде не показывают линии невидимого контура. Границей между внешним видом и разрезом служит штрихпунктирная ось симметрии. Изображение разреза детали располагается от вертикальной оси симметрии справа (рис. 5.8), а от горизонтальной оси симетрии – снизу (рис. 5.9, 5.10) независимо от того на какой плоскости проекций он изображается.

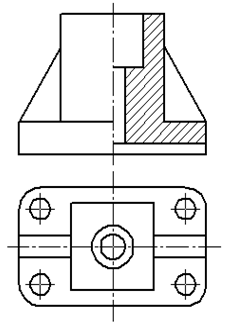
Рис. 5.8

Рис. 5.9 Рис. 5.10

Если на ось симметрии попадает проекция ребра, принадлежащего внешнему очертанию предмета, то разрез выполняют, как показано на рис. 5.11, а если на ось симметрии попадает ребро, принадлежащее внутреннему очертанию предмета, то разрез выполняют, как показано на рис. 5.12, т.е. и в том, и в другом случае проекцию ребра сохраняют. Границу между разрезом и видом показывают сплошной волнистой линией.

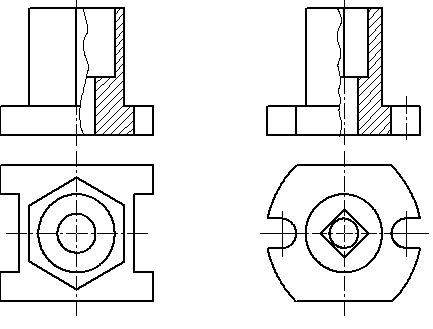
Рис. 5.11 Рис. 5.12

2. На изображениях симметричных деталей, чтобы показать внутреннее устройство в аксонометрической проекции, делают вырез 1/4 части (наиболее освещенной и приближенной к наблюдателю рис. 5.8). Этот вырез не связывают с разрезом на ортогональных проекциях. Так, например, на горизонтальной проекции (рис. 5.8) оси симметрии (вертикальная и горизонтальная) делят изображение на четыре четверти. Выполняя разрез на фронтальной проекции, как бы удаляют нижнюю правую четверть горизонтальной проекции, а на аксонометрическом изображении удаляют нижнюю левую четверть модели. Ребра жесткости (рис. 5.8), попавшие в продольный разрез на ортогональных проекциях, не заштриховывают, а в аксонометрии заштриховывают.

3. Построение модели в аксонометрии с вырезом одной четверти показано на рис. 5.13. Построенная в тонких линиях модель мысленно разрезается фронтальной и профильной плоскостями, проходящими через оси Ох и Оy. Заключенную между ними четверть модели удаляют, становится видна внутренняя конструкция модели. Разрезая модель, плоскости оставляют на ее поверхности след. Один такой след лежит во фронтальной, другой в профильной плоскости разреза. Каждый из этих следов представляет собой замкнутую ломаную линию, состоящую из отрезков, по которым плоскость разреза пересекается с гранями модели и поверхностью цилиндрического отверстия. Фигуры, лежащие в плоскости разреза, в аксонометрических проекциях заштриховывают. На рис. 5.6 показано направление линий штриховки в изометрической проекции, а на рис. 5.7 – в диметрической проекции. Линии штриховки наносят параллельно отрезкам, отсекающим на аксонометрических осях Ох, Оy и Оz от точки О в изометрической проекции одинаковые отрезки, а в диметрической проекции на осях Ох и Оz – одинаковые отрезки и на оси Оy – отрезок, равный 0,5 отрезка на оси Ох или Оz.

4. В данном задании наглядное изображение детали рекомендуется выполнить в диметрической проекции.

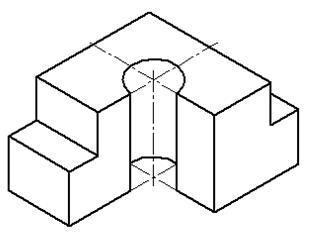
Рис. 5.13

5. При определении истинного вида сечения надо воспользоваться одним из способов начертательной геометрии: вращения, совмещения, плоскопараллельного перемещения (вращения без указания положения осей) или перемены плоскостей проекций.

На рис. 5.14 дано построение проекций и истинного вида сечения фронтально-проецирующей плоскостью Г четырехугольной призмы способом перемены плоскостей проекций. Фронтальной проекцией сечения будет линия, совпадающая со следом плоскости. Для нахождения горизонтальной проекции сечения находим точки пересечения ребер призмы с плоскостью (точки А, В, С, D), соединяя их, получим плоскую фигуру, горизонтальная проекция которой будет А₁, В₁, С₁, D₁.

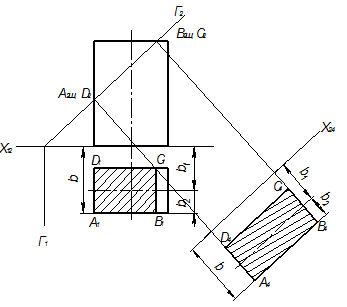Рис. 5.14

Для нахождения истинного вида сечения заменим горизонтальную плоскость проекций новой, параллельной плоскости сечения. Новая ось проекций х14 будет параллельна фронтальному следу плоскости Г (Г1). Новая горизонтальная проекция, например, точки А, (А4) будет находиться от оси х14 на расстоянии b, равном расстоянию от оси х12 до прежней горизонтальной проекции А1 точки А. Ось

симметрии, параллельная оси х₁₂, также будет параллельна новой оси и находиться от нее на расстоянии, равном b₁. В новой системе плоскостей проекций расстояния точек до оси симметрии сохраняют одинаковыми, как и в прежней системе, поэтому для нахождения их можно откладывать расстояния (b₂) от оси симметрии. Соединяя полученные точки А₄В₄С₄D₄, получим истинный вид сечения плоскостью Г заданного тела.

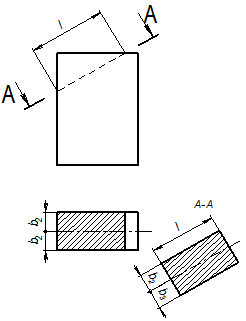Рис. 5.15

В машиностроительном черчении проецирующая плоскость задается лишь одним следом – линией сечения и обозначается буквами русского алфавита, например А-А (рис. 15). Оси симметрии не проводят. Построение сечения начинают с проведения линии симметрии истинного вида сечения, параллельной следу плоскости, располагая его на свободном месте чертежа (рис. 5.15). Если сечение не имеет оси симметрии, то проводят линию, параллельную следу плоскости, от которой и ведут построение фигуры.

На рис. 5.16 дано построение истинного вида сечения усеченного конуса. Большая ось эллипса определяется точками 1 и 2, малая ось эллипса перпендикулярна к большой оси и проходит через ее середину, т.е. точку О. Малая ось лежит в горизонтальной плоскости основания конуса и равна хорде окружности основания конуса, проходящей через точку О.

Эллипс ограничивается прямой линией пересечения секущей плоскости с основанием конуса, т.е. прямой линией, проходящей через точки 5 и 6. Промежуточные точки 3 и 4 построены с помощью горизонтальной плоскости Г. На рис. 5.17 дано построение сечения детали, состоящей из геометрических тел: конуса, цилиндра, призмы.

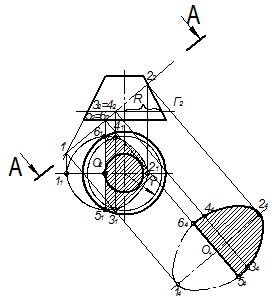Рис. 5.16

Рис. 5.17

в) Сложные разрезы (сложный ступенчатый разрез).

Содержание задания.

Построить третий вид детали по двум данным, выполнить указанные сложные разрезы, построить наклонное сечение плоскостью, заданной на чертеже, проставить размеры, выполнить наглядное изображение детали в аксонометрической проекции (прямоугольная изометрия или диметрия). Задание взять из таблицы 8. Образец выполнения задания (рис. 5.21). Графическую работу выполнить на двух листах чертежной бумаги формата А3.

Методические указания.

1. При выполнении графической работы надо обратить внимание на то, что сложный ступенчатый разрез изображается по следующему правилу: секущие плоскости как бы совмещают в одну плоскость. Границы между секущими плоскостями не указывают, а данный разрез оформляют также, как простой разрез, выполненный не по оси симметрии.

2. В задании часть размеров из-за отсутствия третьего изображения размещена недостаточно целесообразно, поэтому размеры необходимо нанести в соответствии с указаниями, приведенными в разделе «Нанесение размеров», а не копировать с задания.

3. На рис. 5.21. показан пример выполнения изображения детали в прямоугольной изометрии со сложным вырезом.

г) Сложные разрезы (сложный ломаный разрез).

Содержание задания.

Построить третий вид детали по двум данным, выполнить указанный сложный ломаный разрез, проставить размеры. Задание взять из таблицы 9. Образец выполнения задания (рис. 5.22).

Графическую работу выполнить на листе чертежной бумаги формата А4.

Методические указания.

На рис. 5.18 показано изображение сложного ломаного разреза, полученного двумя пересекающимися профильно-проецирующими плоскостями. Чтобы получить разрез в неискаженном виде при сечении предмета наклонными плоскостями, эти плоскости вместе с принадлежащими им фигурами сечения поворачивают вокруг линии пересечения плоскостей до положения, параллельного плоскости проекций (на рис. 5.18 – до положения, параллельного фронтальной плоскости проекций). Построение сложного ломаного разреза основано на способе вращения вокруг проецирующей прямой (см. курс начертательной геометрии). Наличие изломов в линии сечения не отражается на графическом оформлении сложного разреза – он оформляется как простой разрез.

Рис. 5.18

Варианты индивидуальных заданий. Таблица 6 (Построение третьего вида).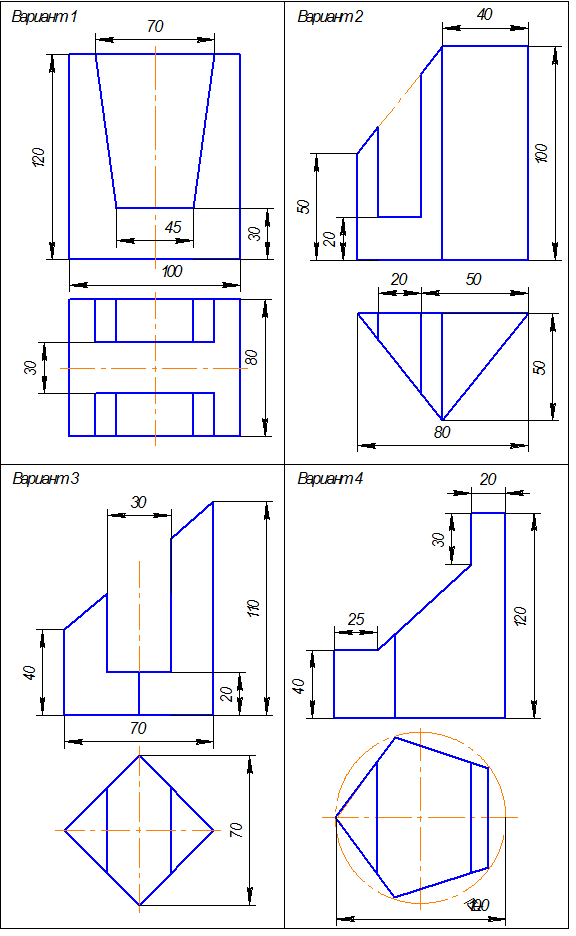

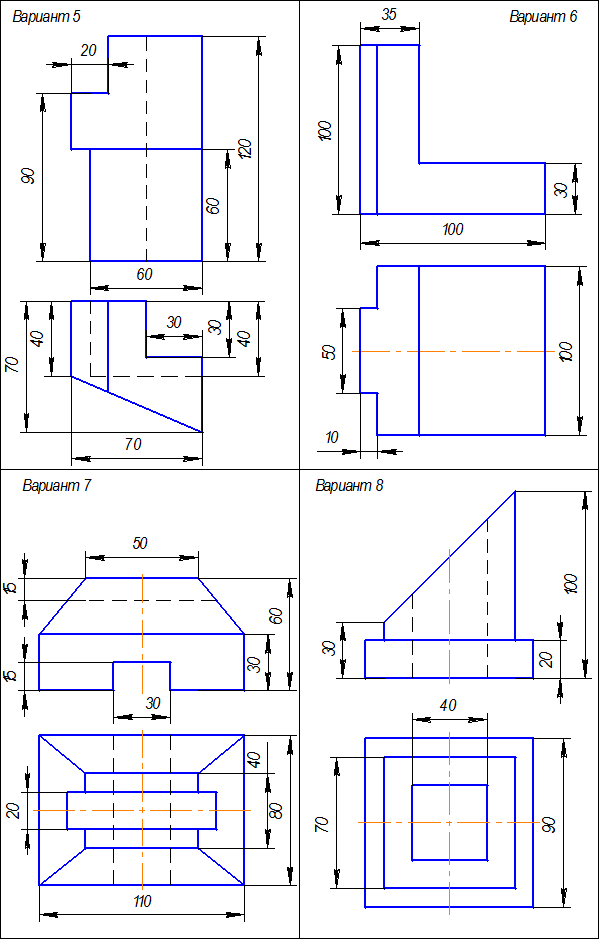
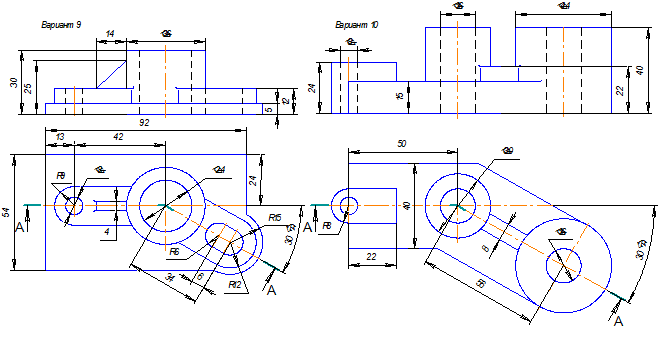
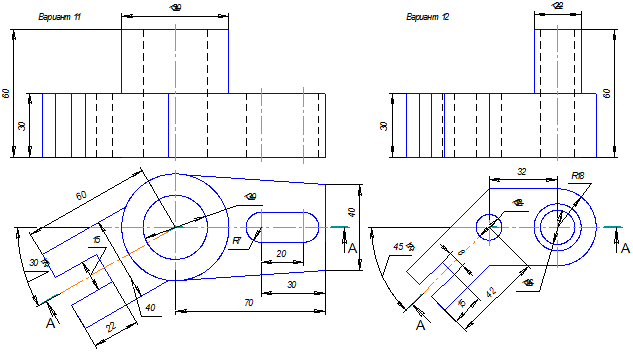
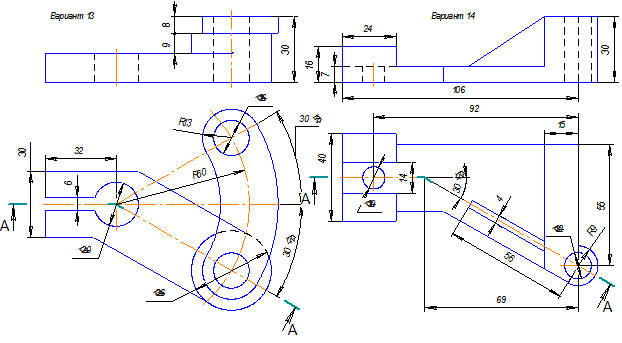
Таблица 7. Простые разрезы. Варианты заданий.

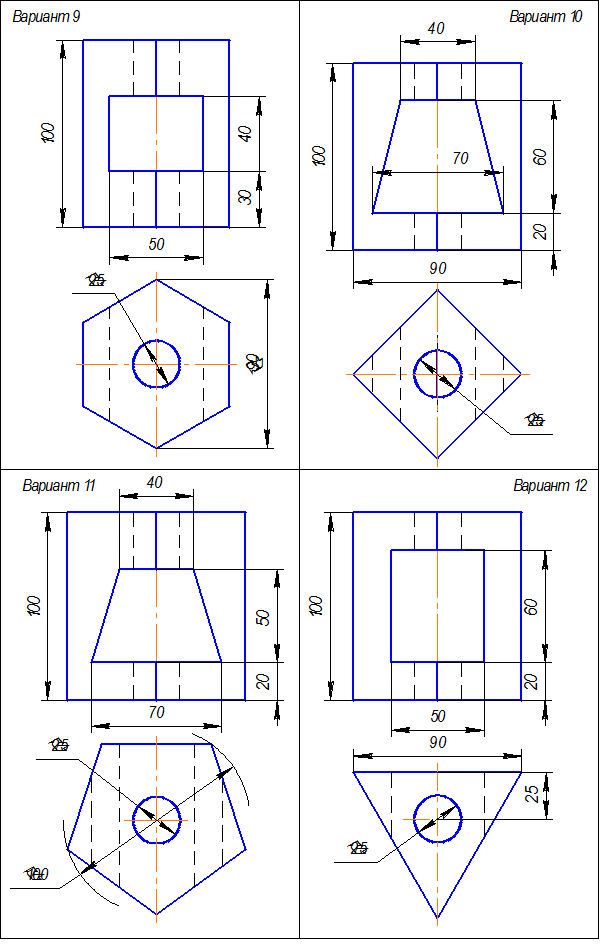
Таблица 8. Сложные ступенчатые разрезы. Варианты заданий.

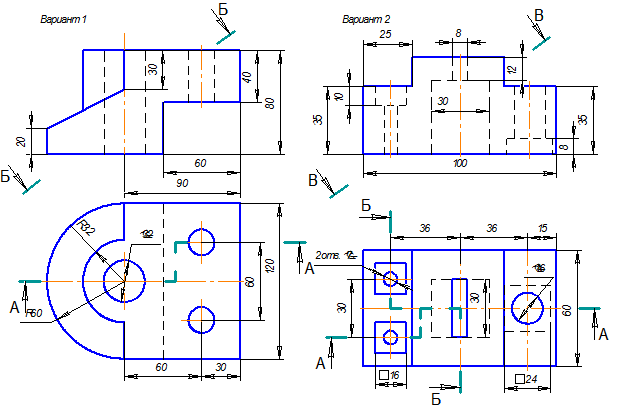
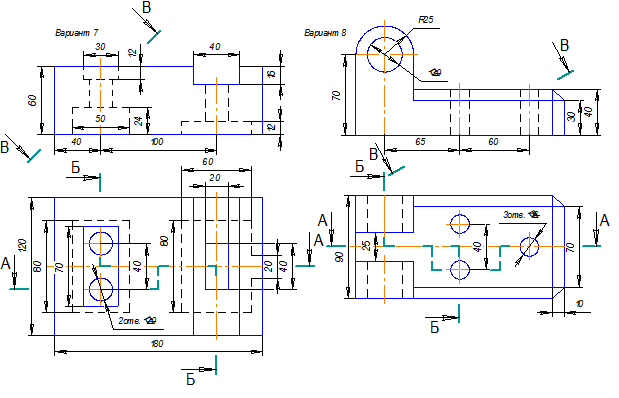
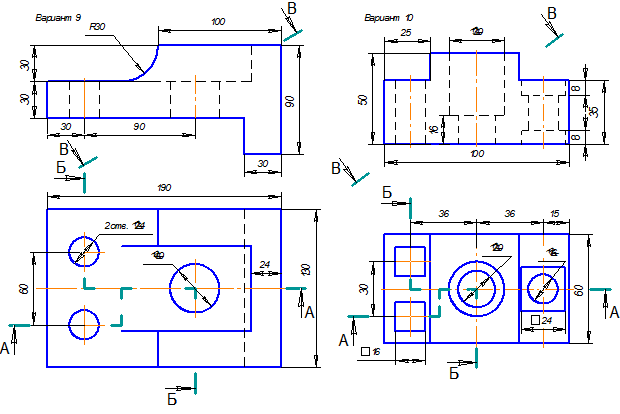
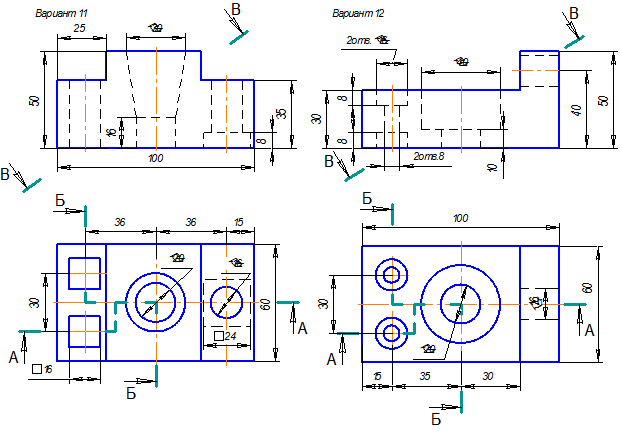
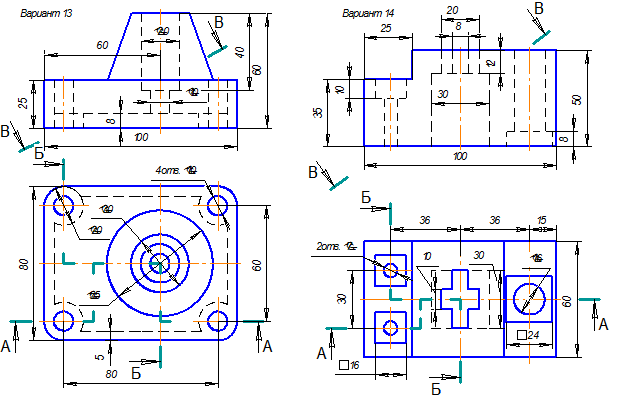
Таблица 9. Сложные ломаные разрезы. Варианты заданий.

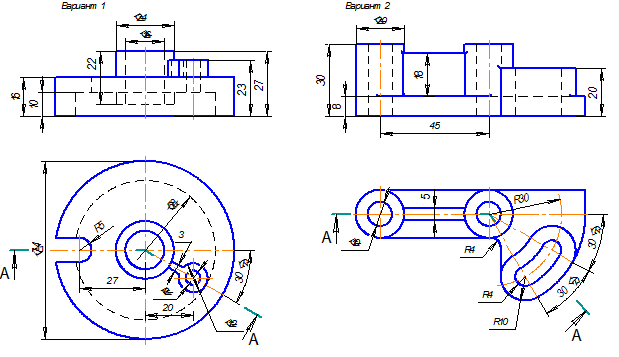
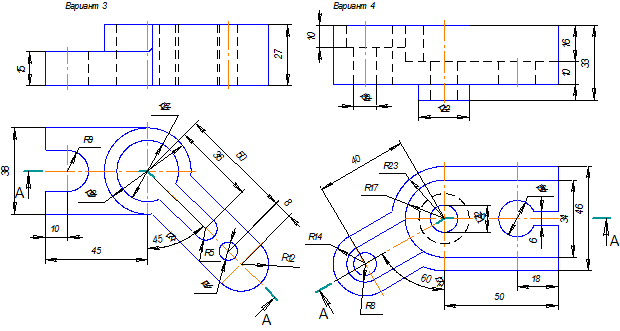
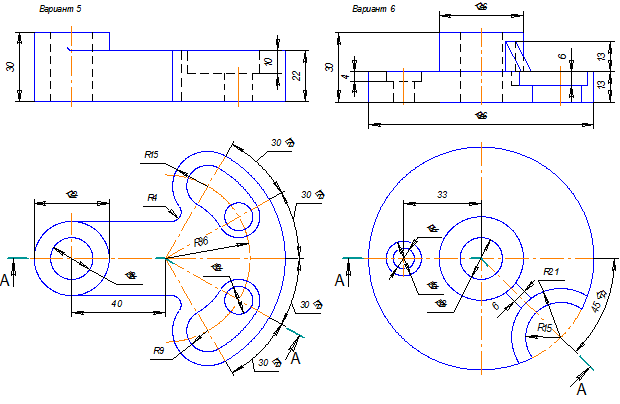
Примеры выполнения задания.

Рис. 5.19

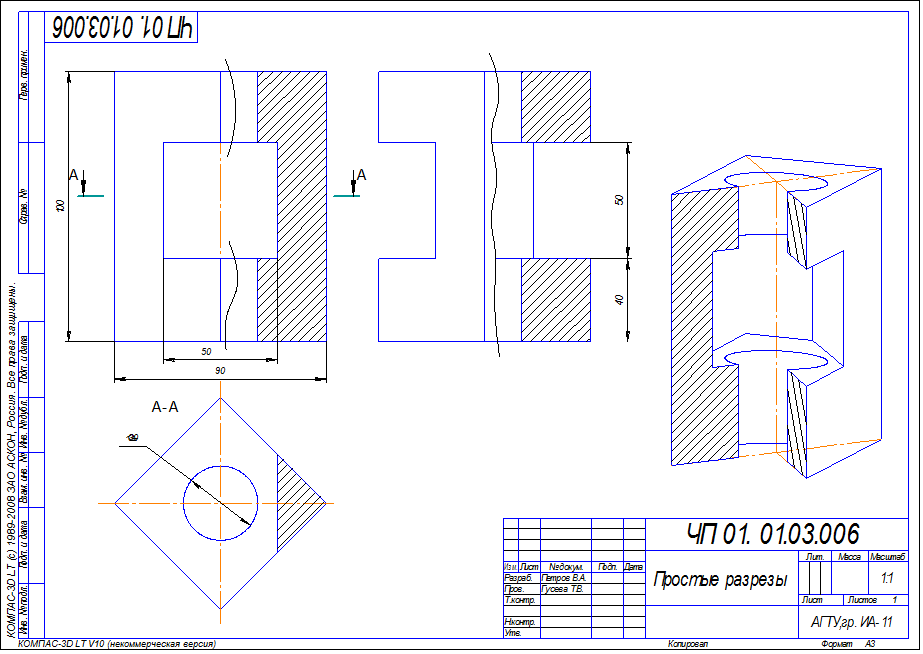
Рис. 5.20

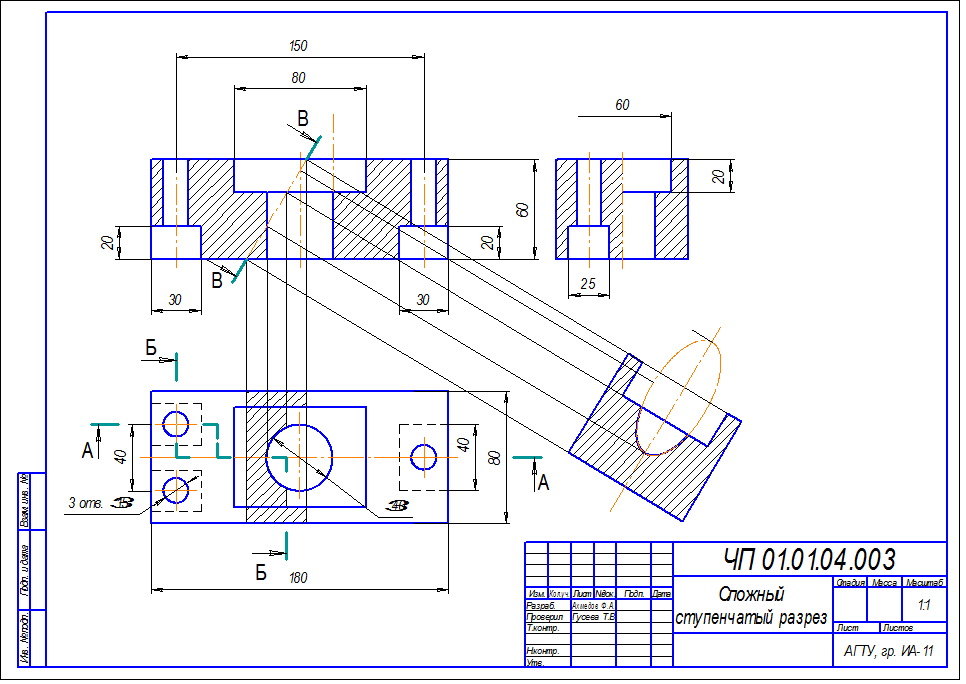
Рис. 5.21

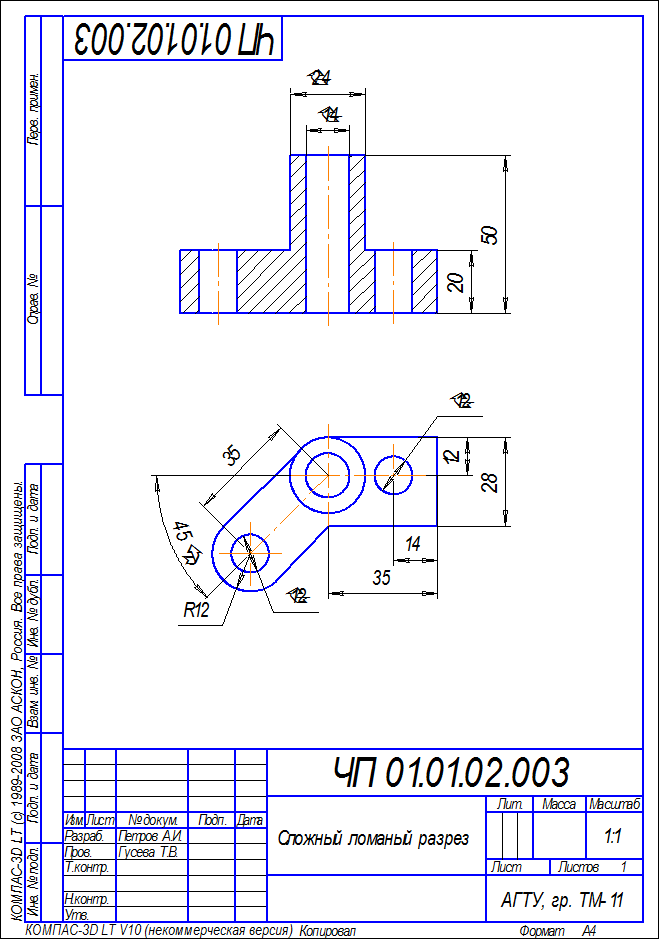Рис. 5.22

Дата добавления: 2015-06-28