Краткая теория. Цель работы: Измерить объёмный расход жидкости в горизонтальных трубках

ИЗМЕРЕНИЕ ОБЪЁМНОГО РАСХОДА ВЯЗКОЙ ЖИДКОСТИ

ЦЕЛЬ РАБОТЫ: Измерить объёмный расход жидкости в горизонтальных трубках. Исследовать зависимость объёмного расхода от разности давлений на концах трубки, длины трубки и радиуса её сечения.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: Установка для определения объемного расхода жидкости.

Одним из основных уравнений, описывающих движение жидкостей и газов, является уравнение Бернулли:

,

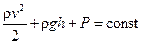где  - плотность жидкости, P - давление, v - скорость жидкости, h - высота уровня жидкости в трубе. Однако при выводе этого уравнения не учитывалась вязкость жидкости. Это приводит к тому, что при стационарном (установившемся) течении жидкости по горизонтальной трубке постоянного сечения давление вдоль оси трубки не изменяется. В реальности, для осуществления стационарного течения жидкости в горизонтальной трубке необходимо поддерживать определённую разность давлений (P ₁ – P ₂) на концах трубки. В свою очередь, разность давлений зависит от длины l и радиуса R сечения трубки, а также от вязкости жидкости h.

Вязкостью, или внутренним трением, называется появление сил трения между слоями жидкости или газа, движущимися параллельно друг другу с разными скоростями, что приводит к переносу импульсов упорядоченного движения молекул. Вязкость относится к явлениям переноса – необратимым процессам, возникающим при нарушении равновесия в физической системе и стремящимся привести систему в равновесное состояние. Каждое из явлений переноса (внутреннее трение, диффузия, теплопроводность) связано с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоёв вещества. Например, в химически однородном газе диффузия есть перенос массы газа из области с большей плотностью в область с меньшей плотностью. А теплопроводность осуществляется в макроскопически неподвижной неравномерно нагретой среде и представляет собой перенос энергии в форме теплоты.

Все эти явления молекулярно-кинетическая теория объясняет хаотическим тепловым движением частиц системы и неодинаковыми значениями какой-либо величины в разных частях системы (пространственная неоднородность её состава вызывает диффузию, разность температур – теплопроводность, разность скоростей её слоёв – вязкость).

Рассмотрим подробнее течение вязкой несжимаемой жидкости по цилиндрической горизонтальной трубке радиусом R. Линии тока при ламинарном течении (т.е. при медленном движении жидкости можно считать течение упорядоченным) параллельны оси. Пусть ось «х», рис. 1, совпадает с осью трубки и направлена в сторону течения жидкости. В объёме трубки выберем горизонтальный цилиндрический слой жидкости толщиной dr, произвольного радиуса r, ось симметрии которого совпадает с осью «x», рис. 1.

Поскольку жидкость несжимаема, а поток стационарный, то объём жидкости, втекающей в выбранный слой (через сечение с координатой x), будет равен объёму жидкости, вытекающей из этого слоя (через сечение с координатой x + dx). Другими словами, скорость втекания равна скорости вытекания. Это значит, что скорость жидкости в любом цилиндрическом горизонтальном слое не зависит от координаты x, но в силу закона вязкого трения должна зависеть от расстояния r данного слоя от оси трубки.

Выделим в трубке произвольный цилиндрический элемент объёма жидкости длиной dx и радиусом r, рис. 2.

Будем считать, что в данном случае выполняется закон вязкого трения И. Ньютона (1687 г.). На боковую поверхность выделенного элемента объёма вдоль направления движения действует сила вязкого трения:

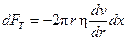
где h - коэффициент динамической вязкости жидкости, 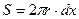- площадь боковой поверхности, 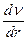- градиент скорости течения (быстрота изменения скорости от слоя к слою). Знак «-» означает, что скорость течения при удалении от оси трубки убывает.

Обозначим давления на торцах цилиндра, как 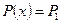и . При установившемся течении сила давления на торцы цилиндра:

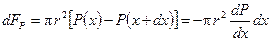
уравновесится силой внутреннего трения 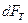, действующей на боковую поверхность цилиндра со стороны внешних слоёв, т.е. 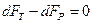, поэтому:

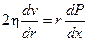(1)

В силу условия стационарности потока v (r) и dv/dr при любом заданном r не должны зависеть от х. А это означает что производная dP/dx должна быть постоянной в любой точке потока и равной (Р ₂ – P ₁) /l, где l - длина трубки, Р ₁ - давление на входе, Р ₂ - давление на выходе трубки. С учетом этого уравнение примет вид:

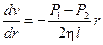(2)

Разделяя переменные и интегрируя, получим:

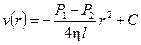(3)

Постоянная интегрирования C находится из граничных условий на стенке трубки, то есть при r = R скорость v должна обращаться в нуль, поскольку сила внутреннего трения о стенку тормозит смежный с ней слой. С учётом этого для v (r) получим выражение:

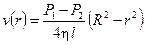(4)

Из формулы (4) следует, что на оси трубки скорость достигает максимальной величины:

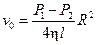(5)

и при удалении от оси меняется па параболическому закону.

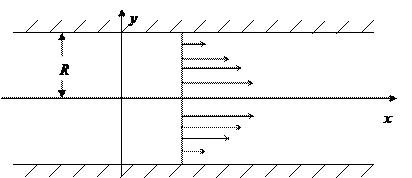В принципе полученное соотношение позволяет находить вязкость газа, если известна скорость его при каком - то радиусе. Однако гораздо проще рассчитать так называемый объёмный расход жидкости Q_V, то есть объём жидкости, протекающей через любое поперечное сечение трубки за единицу времени. В поперечном сечении трубки выделим кольцо радиусом r и толщиной dr. Через него за 1 секунду протекает объём жидкости:

Полный объем жидкости, пересекающей поперечное сечение трубки за 1 секунду, определяется по формуле

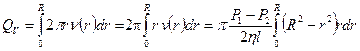(6)

Интегрируя, получаем формулу:

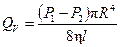(7)

Массовый расход несжимаемой жидкости определяется по формуле:

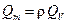(8)

Таким образом, расход жидкости пропорционален разности давлений (Р ₁ - Р ₂), четвертой степени радиуса трубки и обратно пропорционален коэффициенту динамической вязкости  и длине трубки l. Соотношение (7) называется формулой Пуазейля. Оно находит очень широкое применение при теоретическом и экспериментальном исследовании свойств жидкостей. На формуле Пуазейля основаны экспериментальные методы определения коэффициента вязкости жидкости. Она играет важную роль при изучении явления фильтрации жидкости в пористых средах.

Дата добавления: 2015-06-28