Анализ эффективности. Масштабирование и распределение подзадач по процессорам

Масштабирование и распределение подзадач по процессорам

Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и равным объемом передаваемых данных. В случае когда количество столбцов матрицы превышает число процессоров, базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько соседних столбцов (в этом случае исходная матрица A разбивается на ряд вертикальных полос). При соблюдении равенства размера полос такой способ агрегации вычислений обеспечивает равномерность распределения вычислительной нагрузки по процессорам, составляющим многопроцессорную вычислительную систему.

Как и в предыдущем алгоритме, распределение подзадач между процессорами вычислительной системы может быть выполнено произвольным образом.

Пусть, как и ранее, матрица А является квадратной, то есть m=n. На первом этапе вычислений каждый процессор умножает принадлежащие ему столбцы матрицы А на элементы вектора b, после умножения полученные значения суммируются для каждой строки матрицы А в отдельности

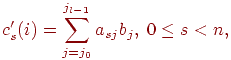
(6.9)

(j₀ и j_l-1 есть начальный и конечный индексы столбцов базовой подзадачи i, 0 i<n). Поскольку размеры полосы матрицы А и блока вектора b равны n/p, то трудоемкость таких вычислений может оцениваться как T'= n²/p операций. После обмена данными между подзадачами на втором этапе вычислений каждый процессор суммирует полученные значения для своего блока результирующего вектора c. Количество суммируемых значений для каждого элемента c_i вектора c совпадает с числом процессоров p, размер блока вектора c на одном процессоре равен n/p, и, тем самым, число выполняемых операций для второго этапа оказывается равным T''=n. С учетом полученных соотношений показатели ускорения и эффективности параллельного алгоритма могут быть выражены следующим образом:

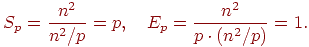
(6.10)

Теперь рассмотрим более точные соотношения для оценки времени выполнения параллельного алгоритма. С учетом ранее проведенных рассуждений время выполнения вычислительных операций алгоритма может быть оценено при помощи выражения

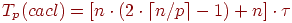
(6.11)

(здесь, как и ранее, τ есть время выполнения одной элементарной скалярной операции).

Для выполнения операции обобщенной передачи данных рассмотрим два возможных способа реализации (см. также лекцию 3). Первый способ обеспечивается алгоритмом, согласно которому каждый процессор последовательно передает свои данные всем остальным процессорам вычислительном системы. Предположим, что процессоры могут одновременно отправлять и принимать сообщения и между любой парой процессоров имеется прямая линия связи, тогда оценка трудоемкости (время исполнения) такого алгоритма обобщенной передачи данных может быть определена как

(6.12)

(напомним, что – латентность сети передачи данных, β – пропускная способность сети, w – размер элемента данных в байтах).

Второй способ выполнения операции обмена данными рассмотрен в лекции 3, когда топология вычислительной сети может быть представлена в виде гиперкуба. Как было показано, выполнение такого алгоритма может быть осуществлено за 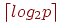шагов, на каждом из которых каждый процессор передает и получает сообщение из n/2 элементов. Как результат, время операции передачи данных при таком подходе составляет величину:

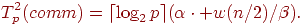
(6.13)

С учетом (6.11) – (6.13) общее время выполнения параллельного алгоритма умножения матрицы на вектор при разбиении данных по столбцам выражается следующими соотношениями.

• Для первого способа выполнения операции передачи данных

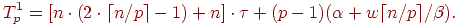
(6.14)

• Для второго способа выполнения операции передачи данных

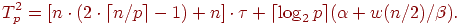
(6.15)

Дата добавления: 2015-06-28