Пример 3. 1 страница

Пример 2.

Пример 1.

Пример 4. Произвести расчёт на прочность при изгибе:

1. Построить эпюры поперечных сил Q_y и изгибающих моментов M_x.

2. Подобрать сечение двутавровой балки по нормальным напряжениям при [δ] = 160 МПа.

3. Для сечен6ия балки, в котором изгибающий момент M_x достигает наибольшего значения, построить эпюры нормальных и касательных напряжений.

4. Для точки перехода стенки в полку определить величины главных напряжений и положения главных площадок.

5. Определить величину прогиба в точке К.

Данные к задаче:

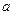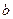m кНм	Р кН	g кН/м		м	м	м
			1,0	1,5	1,2

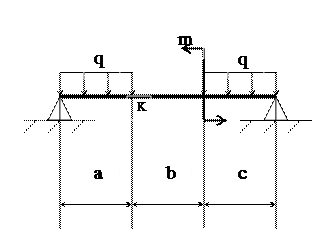
РЕШЕНИЕ:

1. Построим эпюры поперечных сил Q_y и изгибающих моментов М_х.

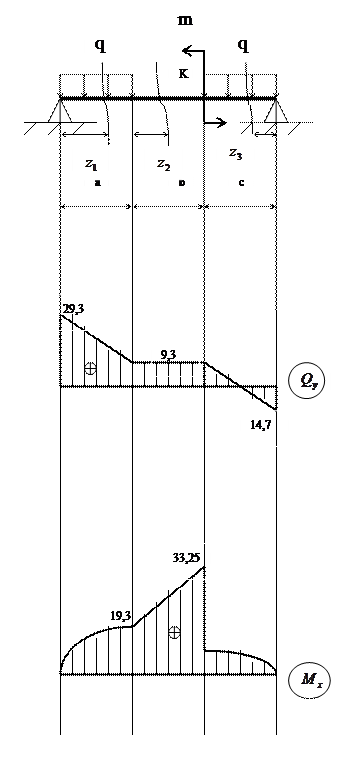
∑М_А = 0

- q ∙ 1 ∙ 0,5 + M – q ∙ 1,2 ∙ (a + b + 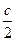) + R_B ∙ 3,7 = 0

- 10 + 30 – 74,4 + R_B ∙ 3,7 = 0

R_B = 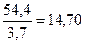кН

∑М_В = 0

q ∙ 1,2 ∙ 0,6 + M + q ∙ 1 ∙ (b + с + 0,5) – R_А ∙ 3,7 = 0

R_А = 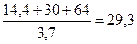кН

Рассмотрим сечение 1 – 1:

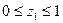
Q_y = R_A – q ∙ z₁ = 29,3 – 20 ∙ z₁ =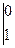

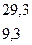
M_x = R_A ∙ z₁ – q ∙ 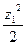= 29,3 ∙ z₁ – 10 ∙ z₁² =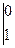

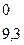
Рассмотрим сечение 2 – 2:

0 ‹ z₁ ‹ 1,5

Q_y = R_A – q ∙ 1 = 29,3 – 20 = 9,3

M_x = R_A ∙ (а + z₂) – q ∙ а ∙ (0,5 + z₂) =

= 29,3 ∙ (1 + z₂) – 20 ∙ (0,5 + z₂) =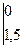

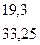
Рассмотрим сечение 3 – 3: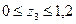

Q_y = R_В + q ∙ z₃ = - 14,7 + 20 ∙ z₃ =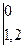

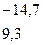
M_x = R_В ∙ z₃ – q ∙ = 14,7 ∙ z₃ – 10 ∙ z₃² =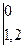

М_х^max = 33,25 кН ∙ м; Q_y = 9,3 кН.

2. Подбираем сечение двутавровой балки по нормальным напряжениям при [ δ ] = МПа.

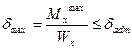
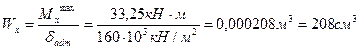
I = 22 W_x = 232 см ³ I_x = 2550 см ⁴ (из таблицы)

h = 22 см

в = 11 см

S = 5,4 мм

t = 8,7 мм

F = 30,6 см²

S_x^max = 131 см² – статический момент полов. фигуры.

S_xⁿ – статический момент полки.

S_xⁿ = S_x^max - S_x^прям = 131 - .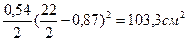

3. Для сечения балки, в котором изгибающий момент M_x достигает наибольшего значения, построим эпюры нормальных и касательных напряжений.

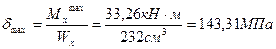‹ 160 МПа

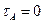
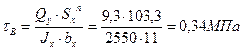
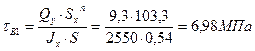
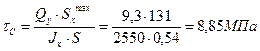
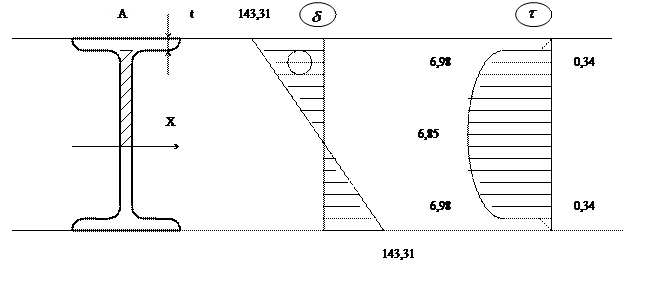
4. Для точки перехода стенки в полку определяем величины главных напряжений, положения главных площадок.

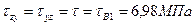
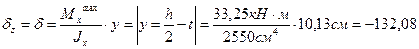
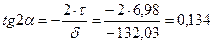
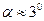
5. Определение величины прогиба в точке К.

;

;

;

;

; ;

; ;

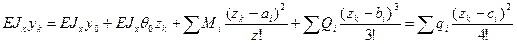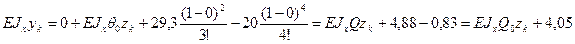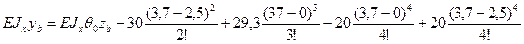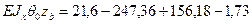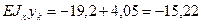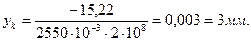
Пример 5. Подобрать сечение стержня, составленного из нескольких профилей соединённых планками или прерывистым сварным швом. Профили располагать так, чтобы сечение было равноустойчиво в отношении обеих главных осей (там, где это условие не соблюдается). Основное допускаемое напряжение [δ] = 160 МПа. Определить расстояние между соединительными планками или швами.

Примечание: Расстояние Н определяется из условия равной гибкости отдельного профиля и всего стержня.

Исходные данные:

F, кН	L, м
	5,00

РЕШЕНИЕ:

Равноустойчивость в направлении главных осей достигается уравнением моментов инерции сечения J_x = J_y. При расчёте можно пользоваться табличным значением момента инерции швеллера J_xТ, а именно J_x = 2J_xТ.

Площадь сечения А = 2А_Т (А_Т – площадь 1 – го швеллера). Радиус инерции сечения:

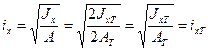
Гибкость: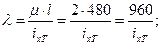

Формула проектирования расчёта:

А = 2А_Т

откуда А_Т

Расчёт производим методом последовательных приближений, приняв:

1) φ₁ = 0,5 А_Т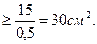

Выбираем швеллер № 24; А_Т1 = 30,6 см²; i_xT1 = 9,73.(Сборник задач по сопротивлению материалов. Под ред. Чернова Ю.В.).

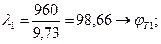
λ = 90 φ = 0,69

λ = 100 φ = 0,6

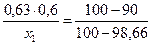
φ_Т1 = 0,6 + 0,012 = 0,612.

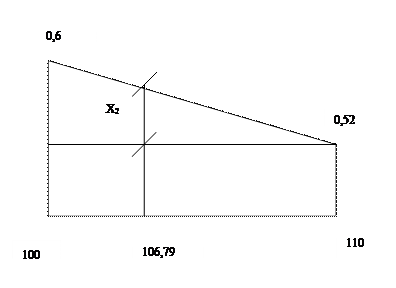2) Второе приближение φ₂ = 0,556 А_Т2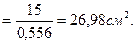

Выбираем швеллер № 22а;

А_Т2 = 28,8 см²; i_xT2 = 8,99.

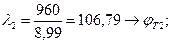
λ = 100 φ = 0,6

λ = 110 φ = 0,52

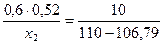
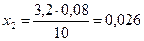
φ_Т1 = 0,52 + 0,026 = 0,546.

3) Третье приближение φ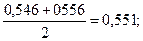₃ = А_Т3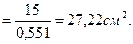

Выбираем швеллер № 22а; А_Т2 = 28,8 см²; i_xT2 = 8,99.

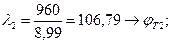
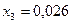
φ₃ = 0,52 + 0,026 = 0,546.

Определяем расчётное напряжение:

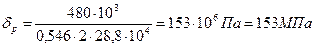
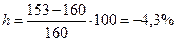
Окончательно выбираем швеллер № 22а:

J_xT^ = 2330 см⁴ J_уT^ = 187 см⁴ 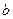= 8,2 см

А_Т = 28,8 см² z₀ = 2,46 см i_yT^ = 2,55 см.

Для всего сечения:

J_x = 2 ∙ J_xT^ = 2 ∙ 2330 = 4660 см⁴

J_у = 2 ∙ [J_уT^ + A_T ∙ (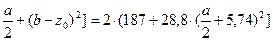

4660 = 2 ∙ [187 + 28,8 ∙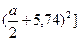

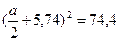
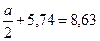
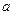= 5,78 см ≈ 58 мм.

Гибкость:

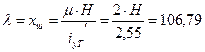
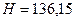см = 1,362 м

n = 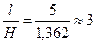пары планок.

Вывод: Необходимы 3 пары планок

Пример 6. Груз весом Q падает на двутавровую балку с высоты h. Допускаемое напряжение для материала балки [δ] = 160 МПа. Определить:

1. Безопасную величину груза из условия прочности.

2. Динамическую деформацию сечения балки в месте падения груза. При определении коэффициента динамичности учесть деформацию пружин, при определении коэффициента динамичности учесть деформацию пружин, присоединённых к балке.

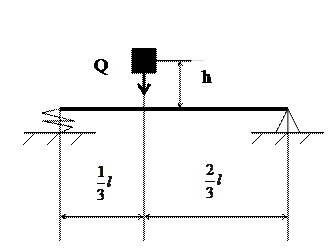Собственный вес балки не учитывать.

Исходные данные:

Номер двутавра	l, м	h, м	δ, м/Н
Wx = 143 cм^3; Jx = 1290 cм^4.	2,4	0,01	20∙10^-7

РЕШЕНИЕ:

Определим реакции в опорах А и В, для чего составим уравнения равновесия:

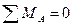- Q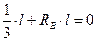

,

,

,

,

,

;

; ;

; ;

;

;

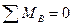
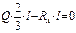
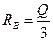
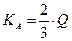
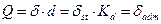
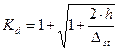
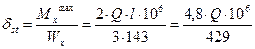
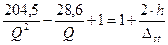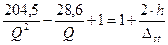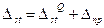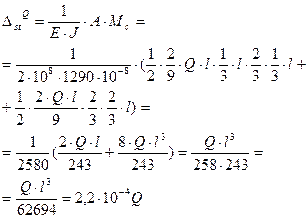
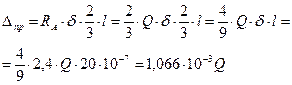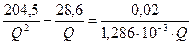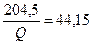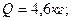
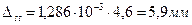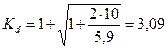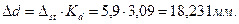
Пример 7. На балке, состоящей из двух двутавровых профилей, установлен двигатель весом Q, делающий n оборотов в минуту. Наибольшее значение возмущающей силы, возникающей вследствие неуравновешенности вращающихся частей двигателя, равно R. Собственный вес балок и силы сопротивления можно не учитывать.

Определить:

1. Частоту собственных колебаний.

2. Частоту изменений возмущающей силы.

3. Вибрационный коэффициент К_В (если коэффициент К_В окажется отрицательным, то в дальнейшем расчёте следует учитывать его абсолютную величину).

4. Коэффициент динамичности при колебаниях К_Д.

5. Наибольшее нормальное напряжение δ_Д.

Если динамическое напряжение окажется больше или намного меньше допускаемого [δ]=100МПа, то необходимо соответственно изменить номер двутаврового профиля, подтвердив правильность выбора нового номера повторным расчётом.

Исходные данные:

Номер двутавра	l, м	Q, кН	R, кН	n, мин^-1
22а Wx = 254 cм^3; Jx = 2790 cм^4	1,6

.

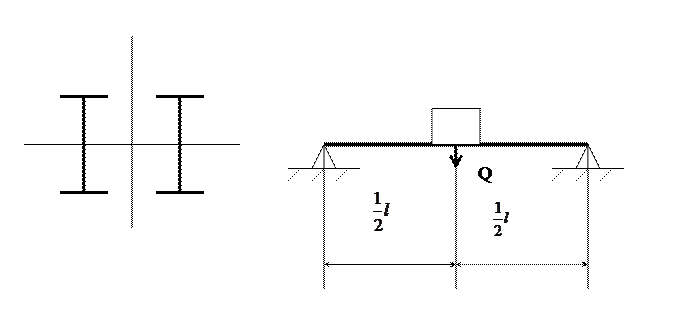РЕШЕНИЕ:

ω₀ =

=

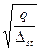
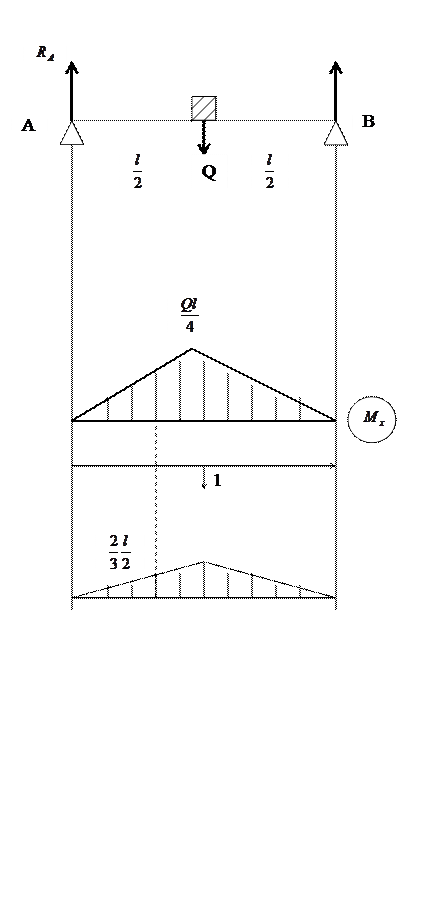
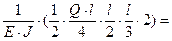
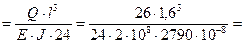
= 3,9 ∙ 10^{-4 м}

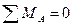
- Q ∙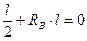

3)Выбираем коэффициент К_В

К_В =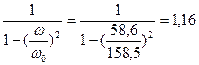

4) Динамический коэффициент

К_d =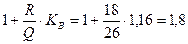

5) Динамическое напряжение

,

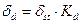где статическое напряжение определяется:

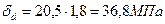, т.к. динамическое напряжение оказалось намного меньше допускаемого [δ]=100МПа, уменьшаем номер двутавра:

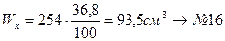
№ 16 W_x = 109 cм³; J_x = 873 cм⁴.

Повторим расчет для двутавра № 16

1)

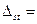
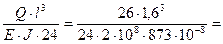
=1,2 ∙ 10^{-3 м}

3) К_В =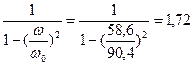

4) К_d =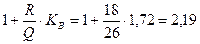

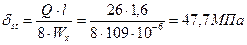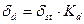
5) ; 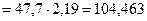МПа

динамическое напряжение оказалось немного больше допускаемого [δ]=100МПа, увеличим номер двутавра:

№ 18 W_x = 143 cм³; J_x = 1290 cм⁴.

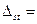
1) 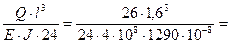8,6∙ 10^{-4 м}

3) К_В =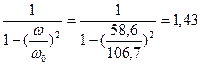

4) К_d =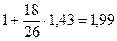

5)

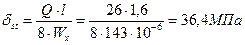
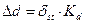
Окончательно выбираем двутавр №18.
Раздел 4. КОНТРОЛЬНЫЕ ЗАДАНИЯ

РАСЧЕТНО-ПРОЕКТИРОВОЧНАЯ РАБОТА №1

Задача №1

1. По данным таблицы определить центр тяжести сечения.

2. Определить центральные моменты инерции: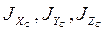

3. Вычислить главные моменты инерции 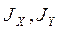, а также угол наклона главных осей инерции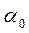

4. Вычислить главные радиусы инерции и построить эллипс инерции.

Указания

Найденный центр тяжести сечения и центры тяжести уголков должны лежать на одной прямой.

Положительное направление угла – против часов стрелки от оси x.

Эллипс инерции строится в одном масштабе с чертежом по 4 точкам.

Все расчеты, таблицы и чертежи должны иметь краткие заголовки и пояснения.

Таблица к задаче №1

Сумма последних двух цифр шифра	ГОСТ 8510-72 Уголок 1	ГОСТ 8509-72 Уголок 2	Расстояние а, см
	250 х 160 х 20	70 х 70 х 8	4,5
	200 х 125 х 16	75 х 75 х 8	4,0
	180 х 110 х 12	80 х 80 х 8	3,5
	160 х 100 х 12	90 х 90 х 8	3,0
	140 х 90 х 10	100 х 100 х 8	2,5
	125 х 80 х 8	110 х 110 х 8	2,0
	110 х 70 х 8	125 х 125 х 8	1,5
	100 х 63 х 8	140 х 140 х 10	1,0
	250 х 160 х 20	70 х 70 х 8	0,5
	200 х 125 х 16	75 х 75 х 8	4,5
	180 х 110 х 12	80 х 80 х 8	4,0
	160 х 100 х 12	90 х 90 х 8	3,5
	140 х 90 х 10	100 х 100 х 8	3,0
	125 х 80 х 8	110 х 110 х 8	2,5
	110 х 70 х 8	125 х 125 х 8	2,0
	100 х 63 х 8	140 х 140 х 10	1,5
	250 х 160 х 20	70 х 70 х 8	1,0
	200 х 125 х 16	75 х 75 х 8	0,5

Схема к задаче №1 выбирается по первой букве фамилии студента.

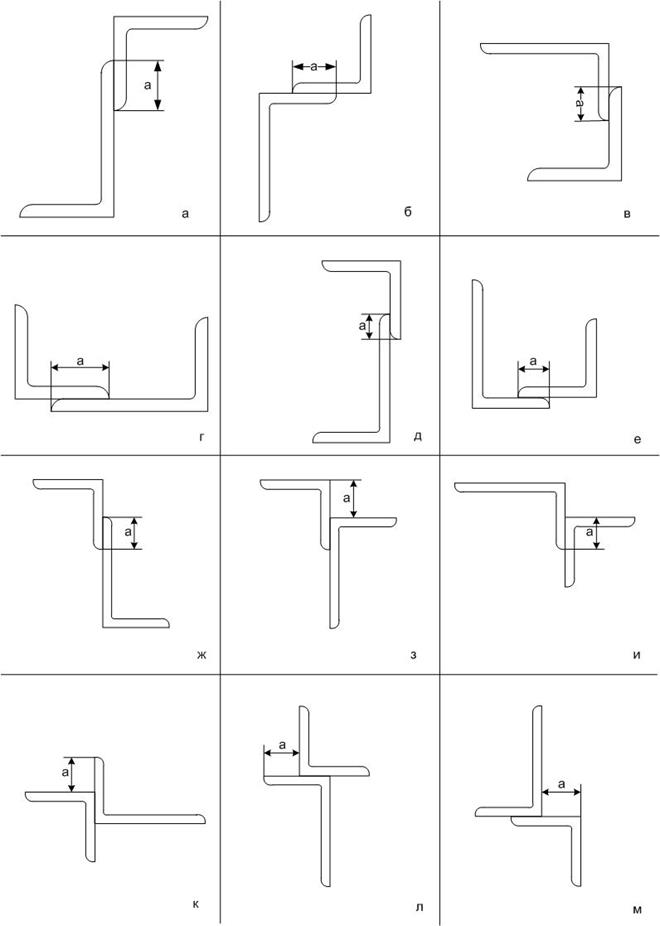
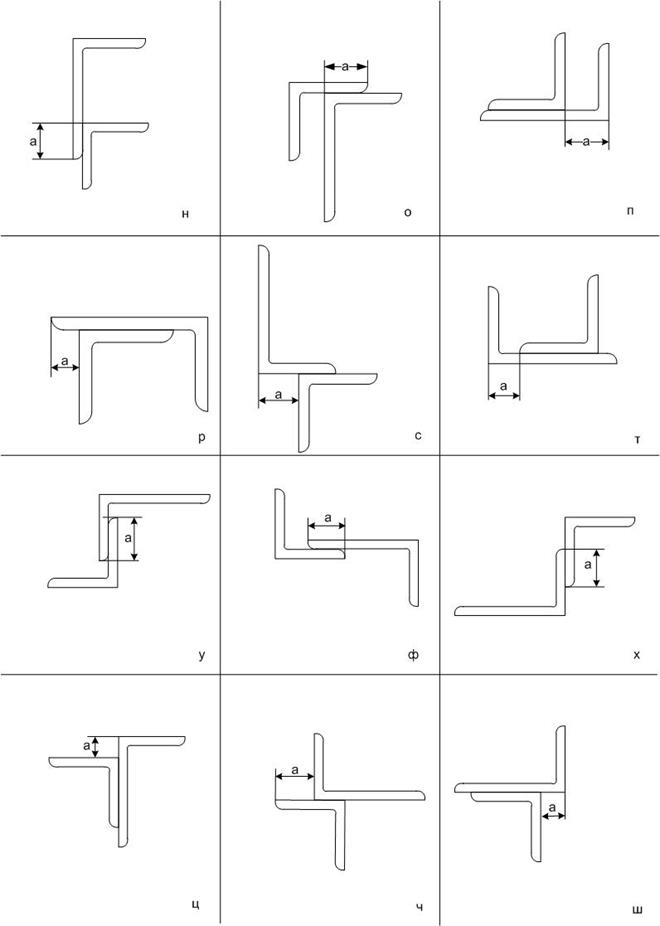
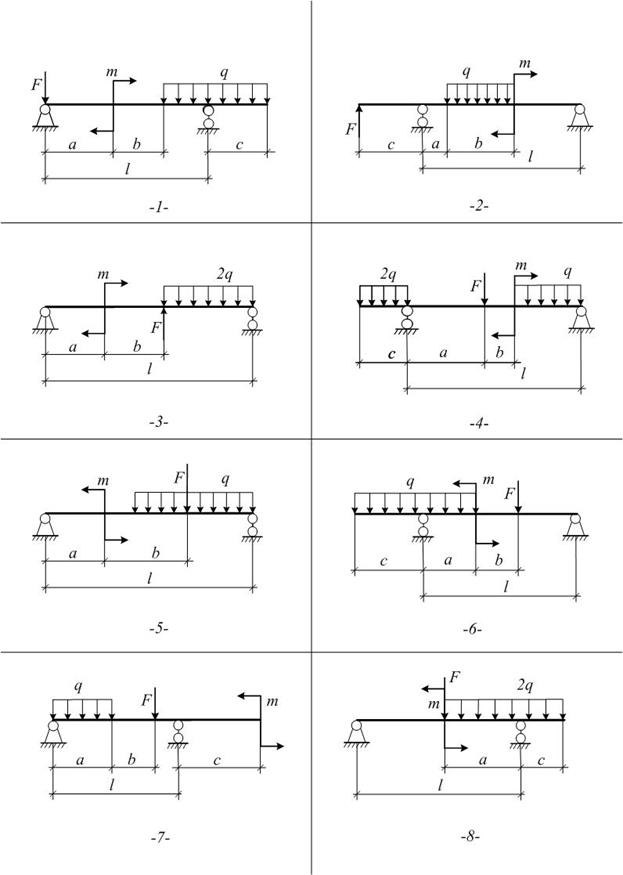
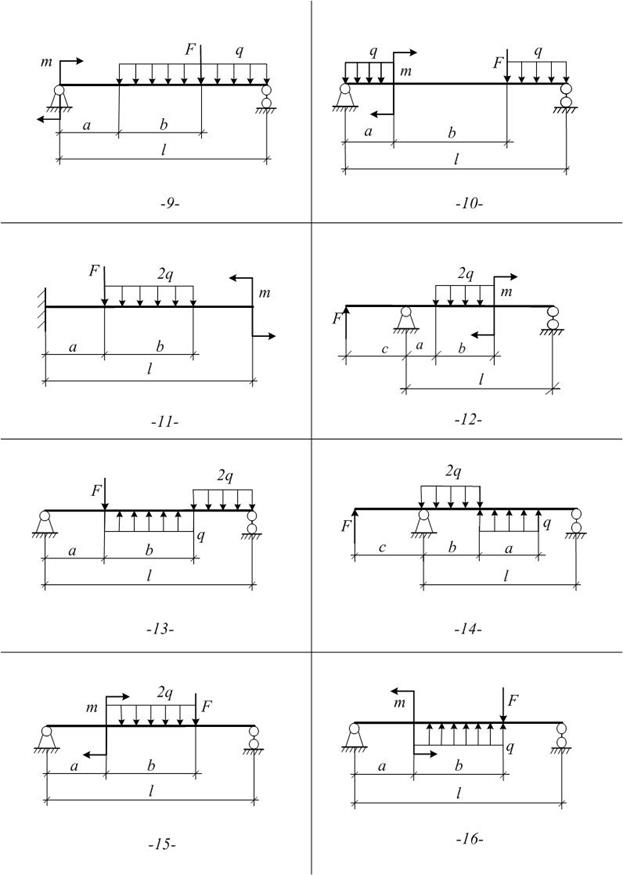
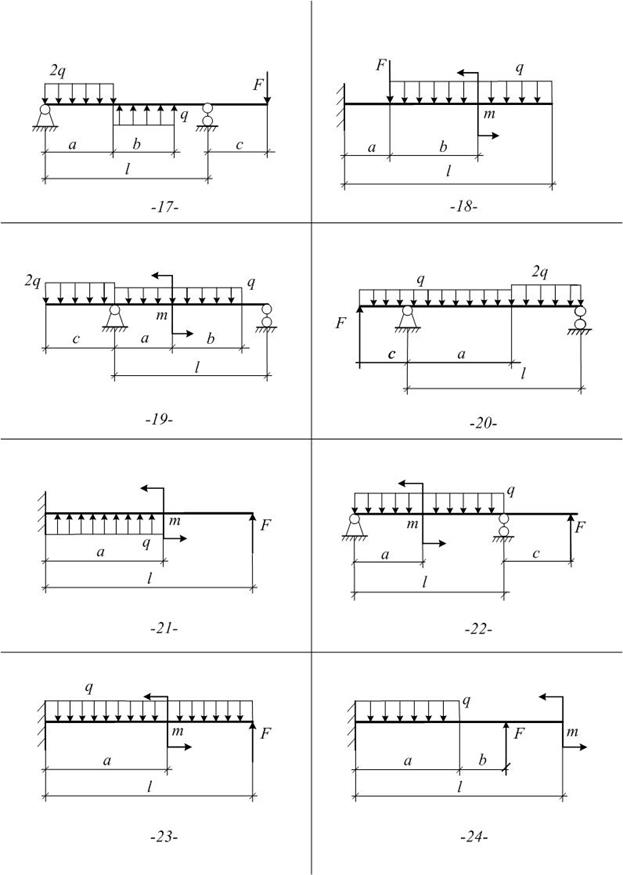
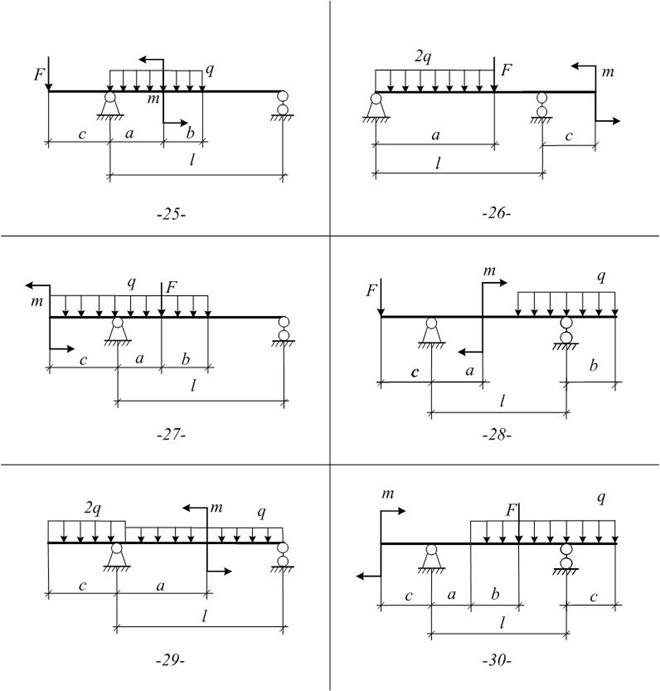
Задача №2

1. Определить опорные реакции с проверкой правильности.

2. Для всех участков составить функциональные зависимости М_х и Q_y от координаты z сечения.

3. На основе вычисленных характерных ординат и использования дифференциальных зависимостей между М_х, Q_y и q построить эпюры внутренних силовых факторов для балки

Таблица к задаче №1

ВАРИАНТЫ РАЗМЕРОВ, м		ВАРИАНТЫ НАГРУЗОК
Предпоследняя цифра шифра	ℓ	а	b	с		Последняя цифра шифра	m, кН·м	F, кН	q, кН/м
	2,8		0,8	0,5
				0,5
	3,2		1,5	0,6
	3,5	1,5		0,6
			1,5	0,8
	4,5	1,5
			1,5
	2,8	0,8		0,5
		1,2	0,8	0,5
	3,2	1,5		0,6

Выбор схемы осуществляется по следующей таблице:

Номер схемы	Предпоследняя цифра шифра
Последняя цифра шифра

Дата добавления: 2015-06-29