Общие сведения. Излагаются основные сведения о режимах течения жидкости в цилиндрической трубе, описание установки и порядок проведения эксперимента

ИД №06430 от 10.12.01

Излагаются основные сведения о режимах течения жидкости в цилиндрической трубе, описание установки и порядок проведения эксперимента.

КУРСК- 2006

В ГОРИЗОНТАЛЬНОЙ ТРУБЕ

Методические указания

к лабораторной работе по гидравлике для студентов, обучающихся по специальностям: 290800, 290700, 290300, 291500, 170600, 120100, 121300, 120500, 150200, 0903, 0905

Составители: Ю.П.Чиков, В.Г.Полищук, В.А.Незнанова

УДК 532 (075.8)

Рецензент

Кандидат технических наук, профессор кафедры

«Теплотехника и гидравлика» В.А.Кудрявцев

Определение режима течения жидкости в горизонтальной трубе: Методические указания к лабораторной работе по гидравлике /сост.: Ю.П.Чиков, В.Г.Полищук, В.А.Незнанова; Курск.гос.техн.ун-т. Курск, 2006.10 с., ил.5, табл. 1. Библиогр.: 10 с.

Предназначены для студентов, обучающихся по специальностям: 290800, 290700, 290300, 291500, 170600, 120100, 121300, 120500, 150200, 0903, 0905.

Подписано в печать Формат 60х84 1/16. Печать офсетная.

Усл.печ. л. Уч.-изд. л. Тираж 100 экз. Заказ. Бесплатно.

Курский государственный технический университет.

Издательско-полиграфический центр Курского государственного технического университета.

305040 Курск, ул. 50 лет Октября, 94.

Цель работы – экспериментальное исследование режима течения в горизонтальной трубе, установленной на гидростенде ГС-3, визуальное наблюдение за сменой режимов течения, отработка практических навыков и углубление знаний студентов.

При течении жидкости любым действующим силам, например, силе вязкого трения Т=μsôdu/drô (здесь μ – динамический коэффициент вязкости, s – площадь трения соседних слоёв, du/dr – градиент скорости в поперечном направлении потока) «противодействует» сила инерции потока F= 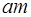(здесь а – ускорение, т - масса рассматриваемого объёма жидкости).

О.Рейнольдс в 1887 году рассмотрел отношение указанных сил, известное впоследствии как безразмерное число Rе, являющееся критерием гидродинамического подобия потоков, находящихся под действием сил вязкого трения,

~ ~ ~ ,

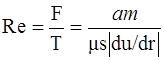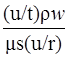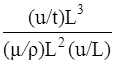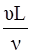где n=μ/ρ – кинематический коэффициент вязкости;

υ – средняя скорость потока;

L – характерный размер потока.

В качестве характерного размера можно применять гидравлический радиус R_г – отношение площади поперечного сечения потока к длине смоченного периметра этого сечения (смоченный периметр – часть периметра сечения потока, на которой жидкость соприкасается со стенками русла – канала, трубы и т.п.). Таким образом, для любого потока

Re=υR_г/n. (*)

Экспериментально установлено, что в природе существуют два режима течения жидкостей: ламинарный (от латинского «ламина» – слой, пластина) и турбулентный (от латинского «турбо» – вихрь). Смена режимов течения происходит при критических значениях числа Рейнольдса Re_кр=580:

- при Re<Re_кр - режим ламинарный;

- при Re>Re_{кр -} режим турбулентный.

Замечания. 1. Re_кр=580 – наиболее употребительное, подтверждаемое многими исследователями “среднее“ значение, хотя в отдельных случаях смена режимов наблюдалась и при Re»100000 (полированные трубы, термоконстантные условия, демпфирование лабораторной установки и др. “искусственные“ условия опытов).

2. Смена режимов зависит от порядка их формирования. Если развивать турбулентный режим из ламинарного, например, постепенно увеличивая скорость потока, критическое значение Re будет превышать, примерно, в пять раз критическое значение Re для случая формирования ламинарного потока из турбулентного. Это объясняется свойством потока “по инерции” сохранять предшествующее состояние.

3. Смена режимов наблюдается при критической скорости υ_кр=Re_кр·ν/R_г, соответствует критическому значению числа Рейнольдса.

4. Следует отметить и существование переходной области между ламинарным и турбулентным режимами, когда течение жидкости носит перемежающийся характер: появляются очаги турбулентности (вихри), скорость в определенной рассматриваемой точке потока то изменяется по величине и направлении, то стабилизируется.

В ламинарном потоке силы трения преобладают над силами инерции и стабилизируют течение, подавляя возмущения, вихри. В результате наблюдается течение слоистое, упорядоченное, без перемешивания жидкости.

Теоретический анализ позволил выявить параболический профиль эпюры скоростей по сечению ламинарного потока в круглой цилиндрической трубе (рис.1), а также соответствующую аналитическую зависимость для эпюры скоростей.

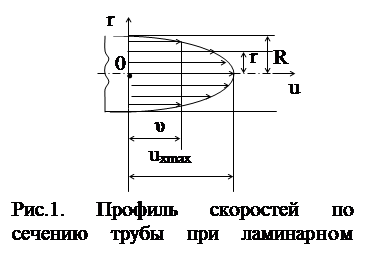Максимальная скорость u_хmax достигается на оси потока, а текущие значения скорости u в любом слое радиусом r определяются соотношением

u/u_max=1-r²/R²,

при этом средняя скорость потока равна половине максимальной (υ=0,5u_max) и жидкость прилипает к внутренней поверхности трубы (υ=0 при r=R).

Многочисленные экспериментальные данные подтверждают приведенные аналитические соотношения для ламинарного потока.

При турбулентном режиме в потоке наблюдаются пульсации параметров, например, изменения во времени продольной скорости в фиксированной точке потока (рис.2).

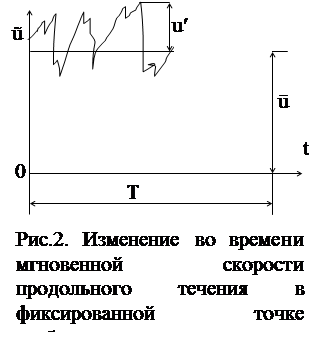Мгновенное значение скорости продольного течения в фиксированной точке турбулентного потока ũ=ū+u′,

где ū – осредненная скорость течения в продольном направлении;

u′ - пульсация скорости продольного течения.

Осредненная скорость – это среднее арифметическое значение мгновенных скоростей:

.

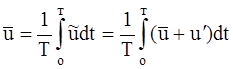Последнее выражение показывает, в частности, что турбулентный поток можно представить как результат наложения двух потоков: одного с осредненной скоростью ū и другого пульсационного со скоростью u′. Пульсационная скорость объясняется хаотичным движением частиц жидкости, многократным пересечением траекторий.

Наряду с пульсациями u′ продольной скорости в турбулентном потоке существуют и поперечные перемещения частиц жидкости. Скорости поперечных перемещений также имеют свои пульсации .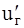

Указанные особенности значительно усложняют анализ турбулентного течения, а отсутствие стройной теории вызывает необходимость использования различных гипотез. Наиболее распространенная из них – гипотеза Л.Прандтля о длине пути смешения, которая позволяет получить значение касательного напряжения трения в виде

.

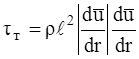Здесь ℓ - длина пути смешения, т.е. расстояние в поперечном направлении потока, на котором частица жидкости сохраняет своё количество движения до попадания в слой с иным значением скорости, а следовательно, и другим количеством движения. Именно это обстоятельство вызывает появление в турбулентном потоке напряжений τ_т силы инерционного трения, которые значительно превышают напряжения силы вязкого трения в ламинарном потоке. С учетом наличия в турбулентном потоке пристенного ламинарного подслоя

.

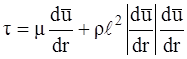Принципиально важным является и то, что турбулентное движение всегда является неустановившимся.

При использовании гипотезы Прандтля был получен логарифмический закон изменения по сечению турбулентного потока осредненной продольной скорости, что в свою очередь позволило выявить изменение коэффициента гидравлического трения λ турбулентного потока также по логарифмическому закону.

Профиль осредненных скоростей по сечению напорного турбулентного потока в круглой цилиндрической трубе представлен на рис.3.

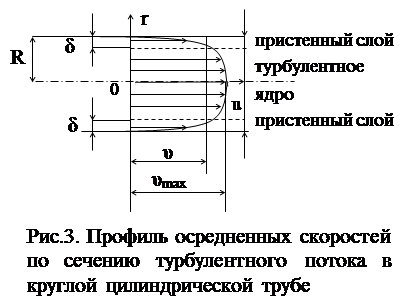Более наполненный профиль осредненных скоростей объясняется пульсационным поперечным движением.

Для упрощения аналитического описания профиля осредненных скоростей турбулентного потока используют закон «одной седьмой»:

.

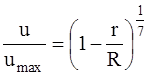Несмотря на наличие мощных вихревых областей (турбулентного ядра потока), вблизи стенки существует ламинарный подслой, толщина которого δ уменьшается с увеличением числа Rе(δ~Re^-1), а градиент скорости в поперечном направлении резко увеличивается, причем

> .

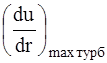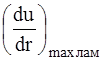В отличие от ламинарного потока величина средней скорости в поперечном сечении турбулентного потока не является постоянной, а изменяется в пределах υ=0,7÷0,9 u_max и с развитием турбулентности (Re®¥) приближается к максимальной (υ®u_max).

В инженерной практике для напорных потоков в круглых цилиндрических трубах в качестве характерного линейного размера применяют не гидравлический радиус, а внутренний диаметр трубы d. Нетрудно подсчитать, что в этом случае

R_г=πR²/(2πR)=R/2=d/4,

а число Рейнольдса Re=υd/ν оказывается в 4 раза большим, чем подсчитанное по формуле (*). Соответственно, в четыре раза увеличивают и критическое значение числа Рейнольдса: Re_кр=4·580=2320.

Дата добавления: 2015-06-29