Общие положения. 13.2. Аналитический способ

РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

План:

13.1. Общие положения

13.2. Аналитический способ

13.3. Способ триангуляции (треугольников)

13.4. Способ нормального сечения

13.5. Способ раскатки

13.6. Приближенные построения разверток

Под развертыванием следует понимать совмещение всей поверхности тела с плоскостью.

РАЗВЕРТКОЙ называется фигура, в которую преобразуется при совмещении с плоскостью поверхность, подразумеваемая как гибкая, но нерастяжимая и несжимаемая пленка.

Развертываемые поверхности могут быть развертывающимися и неразвертывающимися.

К РАЗВЕРТЫВАЮЩИМСЯ относятся такие поверхности, которые могут быть совмещены с плоскостью без разрывов и складок. К этому типу относятся все многогранные поверхности. Разверткой многогранной поверхности является плоская фигура, полученная последовательным совмещением с одной и то же плоскостью всех ее граней. Поэтому построение развертки многогранной поверхности сводится к определению натурального вида ее отдельных граней.

Из кривых поверхностей к числу развертывающихся относятся только те линейчатые поверхности, у которых касательная плоскость во всех точках одной и той же образующей постоянна. Если же у линейчатой поверхности в различных точках одной и той же образующей разные касательные плоскости, то она не развертывается и называется косой поверхностью.

Таким образом, к числу развертывающихся линейчатых поверхностей относятся цилиндрические (рис. 163а), конические (рис. 163б) и торсы (рис. 163в).

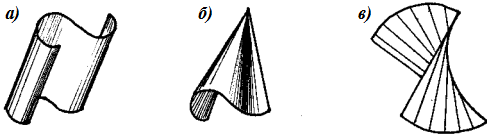
Рис. 163

Все остальные кривые поверхности не развертываются на плоскость и поэтому при необходимости изготовления этих поверхностей из листового материала их приближенно заменяют развертывающимися поверхностями.

СВОЙСТВА РАЗВЕРТОК:

1) каждой точке поверхности соответствует единственная точка ее развертки;

2) длина линии на развертке равна длине соответствующей линии на поверхности;

3) на развертке сохраняются величины плоских углов.

Построение развертки может быть осуществлено различными способами, как аналитически, так и графически.

Дата добавления: 2015-06-29