
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Решение систем с неизвестными множествами
|
|
|
|
Решение систем с неизвестными множествами
Утверждение. (Необходимые и достаточные условия равенства двух множеств).
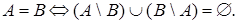
а. 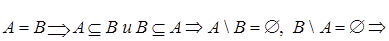
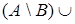
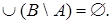
б. 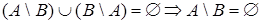 ,
, 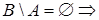
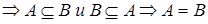 .
.
Рассмотрим систему уравнений, которую в дальнейшем будем называть базовой системой.
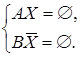 (3)
(3)
Здесь А и В – известные множества, Х – неизвестное множество.
Требуется выразить множество Х через множества А и В и описать необходимые и достаточные условия, которым должны удовлетворять известные множества А и В, чтобы базовая система имела решения. Условие АХ = Æ равносильно включению Х 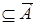 . Условие В
. Условие В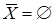 равносильно включению В
равносильно включению В 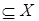 . Эти два включения можно записать в виде одного двойного включения В
. Эти два включения можно записать в виде одного двойного включения В 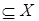
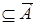 .
.
Тогда обязательно должно быть В 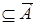 . Если это условие верно, то Х – любое множество такое, что В
. Если это условие верно, то Х – любое множество такое, что В 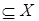 и Х
и Х 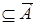 .
.
Покажем, что включение В 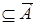 не только необходимо, но и достаточно для существования решения базовой системы.
не только необходимо, но и достаточно для существования решения базовой системы.
Пусть Х – любое множество такое, что В 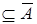 . Тогда
. Тогда
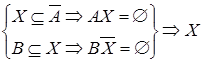 – решение системы (3)
– решение системы (3)
Благодаря доказанным условиям равенства двух множеств, систему уравнений из двух уравнений с одним неизвестным множеством Х и непустыми правыми частями можно свести к эквивалентной ей (с тем же набором решений) базовой системе. Базовую систему мы решать умеем.
Замечание. Запись В 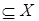
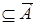 означает, что множество
означает, что множество 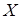 не обязательно однозначно определяется множествами
не обязательно однозначно определяется множествами 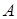 и
и 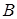 . Если справедливо строгое включение В
. Если справедливо строгое включение В 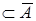 , множество
, множество 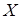 - любое множество такое, что В
- любое множество такое, что В 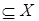
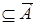 .
.
Приведем несколько примеров решений системы с ненулевыми правыми частями.
Пример 1. Решить систему
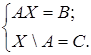
Здесь А, В, С – Данные множества, Х – неизвестное множество.
Требуется выразить множество Х через известные множества А, В, С и записать условия, при которых система имеет решение.
Решение. Воспользуемся доказанным выше критерием равенства двух множеств.
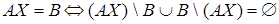
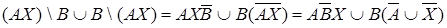 (закон де Моргана) =
(закон де Моргана) = 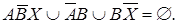
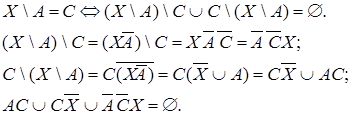
Здесь (и далее), проводя преобразования, мы использовали (и будем использовать) известные свойства операций над множествами.
Очевидно, что объединение нескольких множеств пусто тогда и только тогда, когда каждое из этих множеств – пусто. В результате преобразований получены 6 пустых множеств:
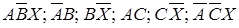 .
.
Рассмотрим сначала множества 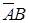 и
и 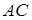 .
.
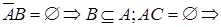 А и С – непересекающиеся множества. На диаграмме Венна множества А, В, С выглядят так (рис.2)
А и С – непересекающиеся множества. На диаграмме Венна множества А, В, С выглядят так (рис.2)
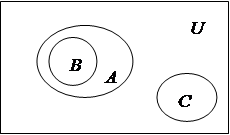

Рис.2
Объединим пустые множества 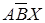 и
и 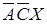
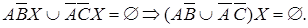
Объединим пустые множества 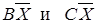 .
.
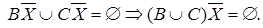
Мы пришли к базовой системе
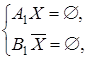
где 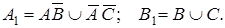 Теперь нужно удовлетворить условию
Теперь нужно удовлетворить условию 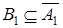 .
. 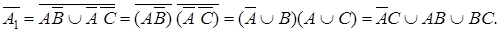
Воспользуемся тем, что 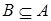 и
и 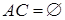 . Отсюда следует, что ВС =Æ; АВ = В;
. Отсюда следует, что ВС =Æ; АВ = В; 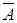 С = С (см. диаграмму Венна).
С = С (см. диаграмму Венна).
Таким образом, 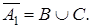 Но и
Но и 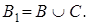 Данная система имеет единственное решение:
Данная система имеет единственное решение: 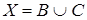 при условии, что В Í А и АС =Æ. Еще раз приведем диаграмму Венна (рис.3).
при условии, что В Í А и АС =Æ. Еще раз приведем диаграмму Венна (рис.3).
|
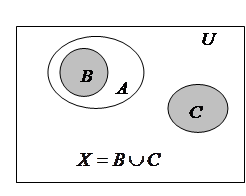
Рис. 3
Пример 2. Решить систему
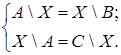
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 684; Нарушение авторских прав?; Мы поможем в написании вашей работы!
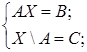 В Í А и АС =Æ.
В Í А и АС =Æ.