Тема: Интегрирование по частям

Если u = u (х), v = v (х) - дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций d(uv) = udv+vdu получается формула интегрирования по частям

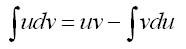
Эта формула применяется в случае, когда подынтегральная функция представляет собой произведение алгебраической и трансцендентной функций. В качестве и обычно выбирается функция, которая упрощается дифференцированием, в качестве dv — оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.

Для сведения данного интеграла к одной из формул простейших интегралов формулу нужно применить несколько раз.

По частям берутся интегралы следующих видов:

1) 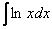- логарифм

2) 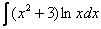- логарифм, умноженный на какой-нибудь многочлен

3) 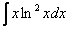– логарифм, умноженный на какой-нибудь многочлен.

4) 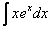, 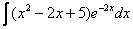– экспоненциальная функция, умноженная на какой-нибудь многочлен.

5) 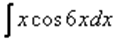, , 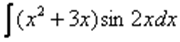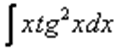– тригонометрические функции, умноженные на какой-нибудь многочлен.

6) 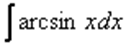, 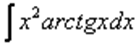– обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.

Пример 1.

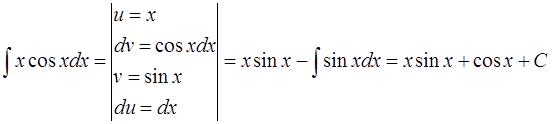
Рекомендации:

В интегралах с подынтегральным выражением вида:

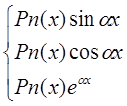(Pn –многочлен степени n)

Pn принимается за u

В интегралах с подынтегральным выражением вида:

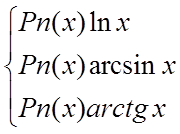
за u ®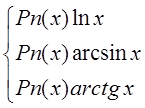

Интегрирование с подстановкой выражений вида 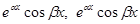после двукратного интегрирования по частям приводится к линейному уравнению относительно вычисляемого интеграла.

Пример 2.Найти неопределенный интеграл.

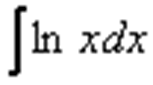
Технически оформление решения реализуется следующим образом, в столбик записываем:

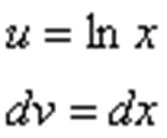
Следующий этап: находим дифференциал :

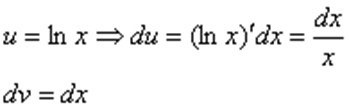
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.

Теперь находим функцию 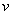. Для того чтобы найти функцию 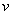необходимо проинтегрировать правую часть нижнего равенства :

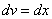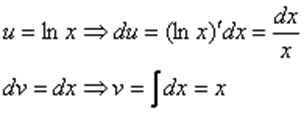
Теперь открываем наше решение и конструируем правую часть формулы: .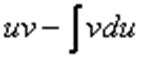
Вот кстати, и образец чистового решения с небольшими пометками:

Пример 3. Найти неопределенный интеграл.

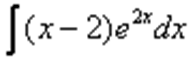
Решение:

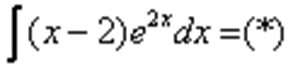
Используя знакомый алгоритм, интегрируем по частям:

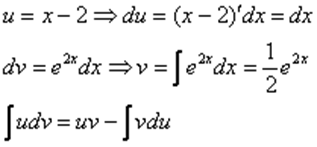
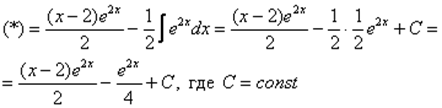
Пример 4. Найти неопределенный интеграл.

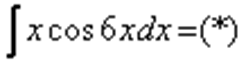
Интегрируем по частям:

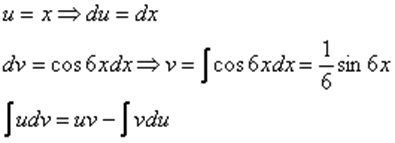
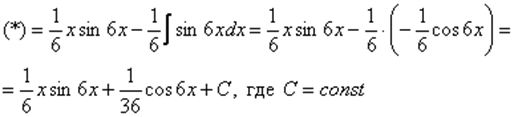
Пример 5. Найти неопределенный интеграл

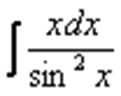
Еще один пример с дробью. Как и в двух предыдущих примерах за 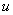обозначается многочлен.

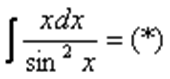
Интегрируем по частям:

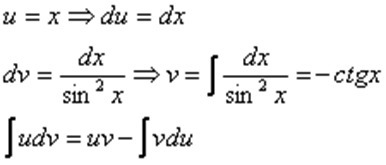
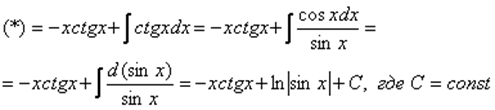
Дата добавления: 2014-01-03