КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика твердого тела
|
|
|
|
16.1. Движение твердого тела.
Определение. Твердое тело - система материальных точек, расстояния между которыми неизменны.
Такое определение справедливо для абсолютно твердого тела, в реальности это приближение.
Для описания движения абсолютно твердого тела обычно вводят две системы координат: лабораторную 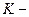 систему с осями
систему с осями 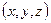 , связанную с точкой
, связанную с точкой 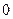 , и систему
, и систему 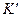 с началом в точке
с началом в точке 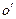 и осями
и осями 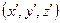 .
.
Штрихованная система отсчета жестко связана с твердым телом, поэтому в лабораторной системе отсчета его положение однозначно определяется положением движущейся 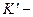 системы отсчета, т.е. положением её начала координат
системы отсчета, т.е. положением её начала координат 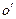 и ориентацией осей
и ориентацией осей 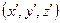 .
.
Т.о., движущаяся 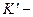 система отсчета и, соответственно, твердое тело описываются тремя компонентами радиус-вектора
система отсчета и, соответственно, твердое тело описываются тремя компонентами радиус-вектора 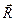 точки
точки 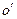 и тремя независимыми углами, определяющими ориентацию осей штрихованной системы координат в лабораторной системе.
и тремя независимыми углами, определяющими ориентацию осей штрихованной системы координат в лабораторной системе.
Говорят, что всякое твердое тело представляет собой механическую систему с шестью степенями свободы.
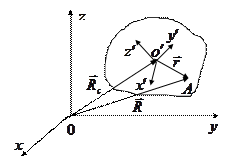 В общем случае движение твердого тела представляет собой
В общем случае движение твердого тела представляет собой
весьма сложный процесс, непосредственное описание которого
может быть сопряжено с практически не преодолимыми
трудностями. Однако законы механики позволяют подойти к
решению этой задачи дифференцированно, рассматривая
движение твердого тела как совокупность совершаемых
одновременно поступательного движения и вращения.
Даже при этом получаемые уравнения (16.2), несмотря на их
кажущуюся простоту представляют собой весьма трудную
задачу.
Общее правило: произвольное движение твердого тела можно представить в виде совокупности поступательного движения всего тела со скоростью 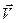 какой-либо его точки
какой-либо его точки 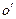 и вращения этого тела вокруг оси, проходящей через эту точку.
и вращения этого тела вокруг оси, проходящей через эту точку.
|
|
|
При этом скорость поступательного движения 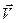 зависит от выбора точки
зависит от выбора точки 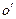 , а скорость вращения (угловая скорость
, а скорость вращения (угловая скорость 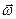 ) от этого выбора не зависит (в этом смысле - абсолютна).
) от этого выбора не зависит (в этом смысле - абсолютна).
Как правило, в качестве точки 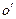 выбирают центр инерции тела, задаваемый в
выбирают центр инерции тела, задаваемый в 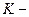 системе радиус-вектором
системе радиус-вектором 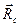 и скоростью его движения
и скоростью его движения 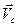 .
.
В этом случае бесконечно малое перемещение любой точки рассматриваемого твердого тела и её мгновенная скорость могут быть определены как
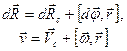 (16.1)
(16.1)
Как для системы материальных точек для твердого тела можно написать два уравнения, которые полностью описывают его движение:
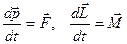 . (16.2)
. (16.2)
Поскольку уравнения (16.2) векторные, то для описания движения твердого тела мы имеем шесть уравнений с шестью переменными. Решение системы этих уравнений позволяет решить задачу о движении твердого тела.
Примечания:
Следует отметить, что только бесконечно малые (элементарные) повороты 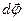 можно рассматривать как векторы. Другими словами, только в этом случае перемещение
можно рассматривать как векторы. Другими словами, только в этом случае перемещение 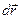 можно представить как векторное произведение
можно представить как векторное произведение
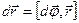 ,
,
поскольку только в пределах бесконечно малого поворота 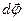 радиус-вектор
радиус-вектор 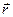 можно считать неизменным. Для малого, но конечного приращения угла поворота
можно считать неизменным. Для малого, но конечного приращения угла поворота 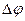 это условия не выполняется.
это условия не выполняется.
16.2. Вращение твердого тела вокруг неподвижной оси. Момент инерции.
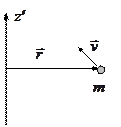 Рассмотрим вращение твердого тела, перейдя в систему центра инерции (
Рассмотрим вращение твердого тела, перейдя в систему центра инерции (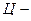 систему).
систему).
В 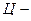 системе твердое тело совершает только вращательное движение вокруг оси, проходящей через точку
системе твердое тело совершает только вращательное движение вокруг оси, проходящей через точку 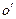 .
.
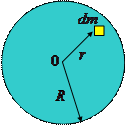
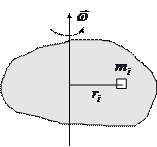
Пусть для определенности вращение происходит вокруг оси 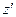 , и эта ось неподвижна. Тогда для материальной точки массой
, и эта ось неподвижна. Тогда для материальной точки массой 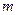 можно записать (см. рис.):
можно записать (см. рис.):
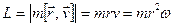 (16.3)
(16.3)
Здесь 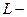 проекция момента импульса этой точки на ось вращения, а
проекция момента импульса этой точки на ось вращения, а 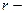 расстояние до оси
расстояние до оси 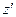 .
.
Момент импульса твердого тела относительно оси 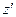 мы получим, если просуммируем по всем материальным точкам системы, имея в виду, что все они вращаются с одинаковой угловой скоростью
мы получим, если просуммируем по всем материальным точкам системы, имея в виду, что все они вращаются с одинаковой угловой скоростью 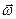 , направленной вдоль оси
, направленной вдоль оси 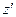 :
:
|
|
|
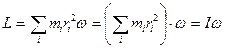 (16.4)
(16.4)
где 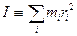 (16.5)
(16.5)
Определение: Величина 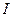 , равная сумме произведений масс материальных
, равная сумме произведений масс материальных
точек системы на квадраты их расстояний до оси вращения, называется
моментом инерции системы относительно этой оси.
Для твердого тела (непрерывное распределение массы) момент инерции
определяется формулой:
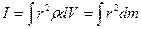 , (16.6)
, (16.6)
где 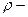 плотность вещества в данной точке,
плотность вещества в данной точке, 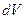 и
и 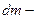 элемент объема и массы тела.
элемент объема и массы тела.
Элемент объема: 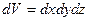 - в декартовой системе координат;
- в декартовой системе координат;
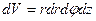 - в цилиндрической системе координат;
- в цилиндрической системе координат;
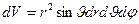 - в сферической системе координат.
- в сферической системе координат.
Свойства момента инерции.
Момент инерции твердого тела зависит от распределения масс относительно интересующей нас оси и является величиной аддитивной.
Момент инерции твердого тела зависит от положения оси вращения.
Сосчитаем моменты инерции некоторых однородных твердых тел относительно их осей симметрии.
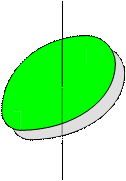
а) Момент инерции тонкого диска радиусом 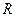 относительно оси вращения, проходящей по диаметру диска.
относительно оси вращения, проходящей по диаметру диска.
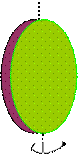 Пусть масса однородного диска
Пусть масса однородного диска 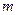 , а его радиус и толщина
, а его радиус и толщина
равны 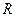 и
и 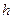 , соответственно, причем
, соответственно, причем 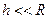 .
.
Момент инерции элементарной массы 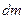 относительно оси,
относительно оси,
проходящей по диаметру диска определяется выражением
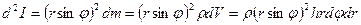 ,
,
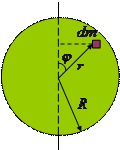 где площадь поверхности элемента
где площадь поверхности элемента 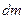 ,
,
лежащей в плоскости рисунка записана
в полярных координатах.
Тогда
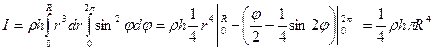
Учитывая, что 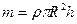 , получаем
, получаем
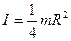 . (16.7)
. (16.7)
б) Момент инерции цилиндра (диска) относительно оси симметрии (проходящей через точку 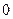 перпендикулярно плоскости рисунка).
перпендикулярно плоскости рисунка).
Пусть масса однородного диска 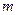 , а его радиус и толщина равны
, а его радиус и толщина равны 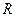 и
и 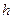 , соответственно.
, соответственно.
Тогда момент инерции элементарной массы 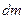 равен
равен
|

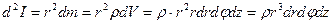 ,
,
где 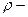 плотность диска,
плотность диска, 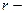 расстояние до оси
расстояние до оси
вращения, а элемент объема взят в цилиндрической
системе координат.
Интегрируя по углу 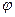 , радиусу
, радиусу 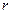 и координате
и координате 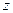 ,
,
и учитывая, что, как и в предыдущем случае,
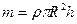 ,
,
находим момент инерции диска (цилиндра):
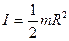 . (16.8)
. (16.8)
в) Момент инерции однородного шара массой 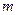 и радиусом
и радиусом 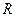 относительно оси, проходящей через его центр.
относительно оси, проходящей через его центр.
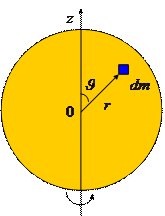
Эту задачу удобнее рассматривать в сферической системе координат, тогда момент инерции элементарного кусочка можно записать как
|
|
|
|
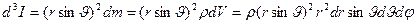 ,
,
где 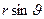 - расстояние кусочка массой
- расстояние кусочка массой 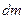 до оси вращения,
до оси вращения, 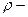 плотность шара. Интегрируя по всем переменным:
плотность шара. Интегрируя по всем переменным:
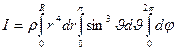
и учитывая, что масса шара равна 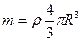 , получаем момент инерции шара относительно оси симметрии:
, получаем момент инерции шара относительно оси симметрии:
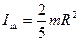 . (16.9)
. (16.9)
16.3. Теорема Штейнера.
Теорема: Момент инерции тела 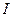 относительно произвольной оси
относительно произвольной оси 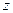 равен сумме момента инерции
равен сумме момента инерции
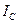 относительно оси
относительно оси 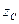 , параллельной данной и проходящей через центр инерции тела, и
, параллельной данной и проходящей через центр инерции тела, и
произведения массы тела на квадрат расстояния между осями.
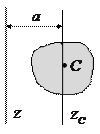
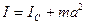 (16.10)
(16.10)
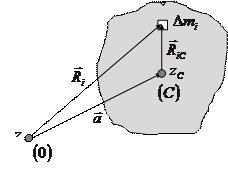
Доказательство теоремы.
Пусть точка 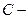 центр инерции тела. Проведем через произвольный элемент
центр инерции тела. Проведем через произвольный элемент 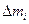 плоскость, перпендикулярную осям
плоскость, перпендикулярную осям 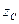 и
и 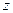 , проходящим через центр инерции тела
, проходящим через центр инерции тела 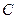 и точку
и точку 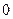 . Векторы
. Векторы 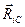 и
и 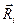 задают, соответственно, положение элемента
задают, соответственно, положение элемента 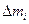 относительно осей
относительно осей 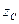 и
и 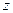 , а вектор
, а вектор 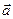 – взаимное расположение этих осей.
– взаимное расположение этих осей.
При этом
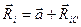 . (16.11)
. (16.11)
Тогда момент инерции относительно оси 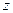 равен
равен
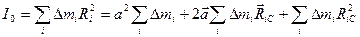 .
.
В этом выражении последнее слагаемое дает момент инерции 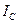
относительно оси 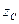 , проходящей через центр инерции тела.
, проходящей через центр инерции тела.
Второе слагаемое равно нулю.
Действительно, 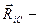 вектор-проекция радиус-вектора
вектор-проекция радиус-вектора 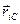 ,
,
определяющего положение элемента 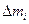 относительно центра
относительно центра
инерции тела, на рассматриваемую плоскость. Относительно
центра инерции вектор 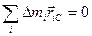 (что следует из определения центра инерции), следовательно, и сумма векторов-проекций также равна нулю:
(что следует из определения центра инерции), следовательно, и сумма векторов-проекций также равна нулю:
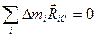 .
.
В первом слагаемом 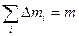 .
.
Итак, теорема Штейнера (16.10) доказана.
Пример. Используя теорему Штейнера, найдем момент инерции диска относительно оси 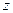 , проходящей через
, проходящей через
его край перпендикулярно плоскости диска:
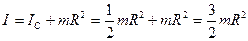 .
.
16.4. Главные моменты инерции.
Вообще говоря, моменты инерции, определенные относительно различных осей, проходящих через центр инерции тела, различны.
|
Ось вращения тела, положение которой в пространстве остается неизменным в отсутствие внешних сил, называют свободной осью тела. Иначе говоря, для сохранения вращения тела вокруг свободной оси не нужно прикладывать внешние силы.
В общей теории доказывают, что для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями.
|
|
|
Такие оси называются главными осями инерции тела, а моменты инерции относительно их называются главными моментами инерции.
Важной особенностью главных осей инерции является то, что при вращении тела вокруг любой из них направление вектора момента импульса 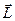 совпадает с направлением вектора угловой скорости тела
совпадает с направлением вектора угловой скорости тела 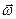 и
и
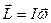 .
.
Для тел с центральной симметрией (шаровые волчки) равны все главные моменты инерции: 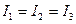 . П ример: шар, куб.
. П ример: шар, куб.
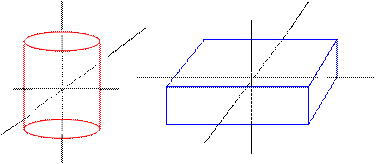
Для тел с осевой симметрией (симметрические волчки) равны два из трех главных моментов инерции: 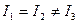 . Пример: цилиндр
. Пример: цилиндр
|
В общем случае (асимметрические волчки) все главные моменты инерции различны: 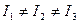 .
.
Пример: параллелепипед.
Вращение вокруг осей, соответствующим максимальным и минимальным значениям моментов инерции, является устойчивым, а вокруг других – неустойчивым. Примеры:
Вращение коробка спичек. При внешнем воздействии наиболее устойчиво то вращение, которое соответствует максимальному значению главного момента инерции.
Вращение диска, закрепленного за край с помощью нити.
Обратим внимание, что главные оси инерции не обязательно проходят через центр инерции тела.
Для несимметричного (или неоднородного) тела момент импульса 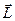 , вообще говоря, не совпадает по направлению с вектором угловой скорости
, вообще говоря, не совпадает по направлению с вектором угловой скорости 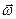 . Из рисунка легко понять, что момент импульса выделенной
. Из рисунка легко понять, что момент импульса выделенной
пунктиром симметричной части тела совпадает по направлению с вектором угловой скорости.
 Однако момент импульса каждой части тела
Однако момент импульса каждой части тела 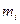 , не входящей в
, не входящей в
мысленно выделенную симметричную, дает дополнительный вклад 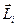
в момент импульса всего тела. Из-за этой “добавки” получаем, что
вектор момента импульса несимметричного (неоднородного) тела,
вращающегося как показано на рисунке, отклоняется от направления
вектора угловой скорости.
При вращении несимметричного (неоднородного) тела момент
импульса 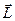 описывает конус, ось которого направлена по вектору
описывает конус, ось которого направлена по вектору
угловой скорости и
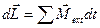 .
.
Но всегда верно соотношение, связывающее проекцию момента импульса на ось вращения, с угловой скоростью 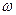 :
:
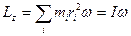 .
.
Если момент инерции тела во время движения не изменяется (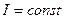 ), то:
), то:
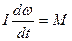 , или
, или 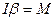 , (16.12)
, (16.12)
где 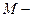 суммарный момент всех внешних сил относительно оси вращения, а
суммарный момент всех внешних сил относительно оси вращения, а
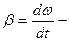
проекция вектора углового ускорения 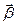 на ось вращения.
на ось вращения.
Итак, при вращении вокруг свободных (главных) осей связь между моментом импульса вращающегося тела и его угловой скоростью наиболее проста:
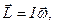
или, если координатные оси (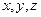 ) совпадают с главными осями вращения:
) совпадают с главными осями вращения:
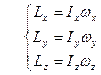 . (16.13)
. (16.13)
Однако если ось вращения не является свободной (главной) и произвольно ориентирована относительно координатных осей (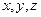 ), то связь между компонентами момента импульса и угловой скорости становится более сложной:
), то связь между компонентами момента импульса и угловой скорости становится более сложной:
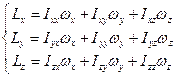 . (16.14)
. (16.14)
Здесь 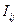 - коэффициенты пропорциональности, имеющие размерность момента инерции.
- коэффициенты пропорциональности, имеющие размерность момента инерции.
Частные случаи:
1) 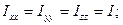 т.е.
т.е. 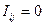 для
для 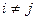 , то
, то 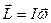 ;
;
2) ось вращения ориентирована вдоль оси 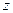 , т.е.
, т.е. 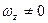 , а
, а 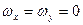 , то
, то 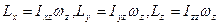 .
.
Совокупность этих 9 величин 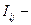 тензор 2-го ранга - тензор инерции:
тензор 2-го ранга - тензор инерции:
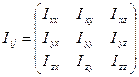 . (16.15)
. (16.15)
Операция, определяемая (16.14), - это умножение вектора 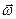 на тензор
на тензор 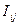 , в результате чего мы получаем новый вектор –
, в результате чего мы получаем новый вектор – 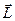 .
.
Короткая запись уравнений (16.14):
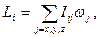
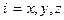 . (16.16)
. (16.16)
Тензор инерции характеризует инертные свойства тела при вращении.
Т.о., для описания вращательного движения твердого тела требуется введение новой математической функции – тензора, который определяется путем задания 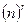 компонент, где
компонент, где 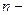 число измерений пространства,
число измерений пространства, 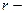 ранг тензора, т.е. в трехмерном пространстве тензор второго ранга определяет совокупность девяти величин. Понятие “тензор” можно распространить на векторы и скаляры, которые в этом случае могут быть определены как тензоры первого и нулевого ранга, соответственно.
ранг тензора, т.е. в трехмерном пространстве тензор второго ранга определяет совокупность девяти величин. Понятие “тензор” можно распространить на векторы и скаляры, которые в этом случае могут быть определены как тензоры первого и нулевого ранга, соответственно.
17.5. Выражения для тензора инерции и его компонент в декартовых координатах.
Найдем выражение для тензора инерции.
Представим момент импульса твердого тела относительно его центра масс как сумму моментов кусочков массой 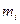 относительно того же начала:
относительно того же начала:
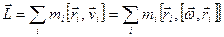 . (16.17)
. (16.17)
Двойное векторное произведение расписываем по известному правилу векторной алгебры:
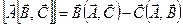 . (16.18)
. (16.18)
Тогда
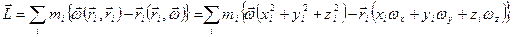
Найдем теперь проекцию вектора 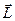 на ось
на ось 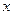 , имея в виду что
, имея в виду что
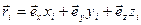 и
и 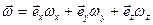 :
:
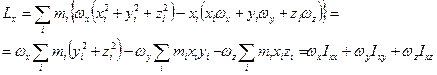
Расписывая аналогично другие проекции вектора 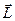 , получаем выражение для тензора момента инерции в виде:
, получаем выражение для тензора момента инерции в виде:
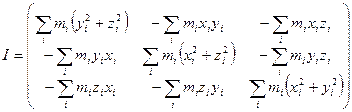 . (16.19)
. (16.19)
Тензор (16.19) симметричный, т.е. 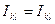 , где
, где 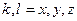 , поэтому он содержит всего шесть независимых компонент.
, поэтому он содержит всего шесть независимых компонент.
Тензор (16.19) и его компоненты вычисляются путем интегрирования по всем элементарным массам, так, например:
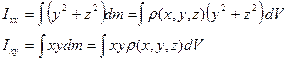 . (16.20)
. (16.20)
Если совместить координатные оси (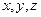 ) с главными осями инерции, то тензор (16.19) становится диагональным:
) с главными осями инерции, то тензор (16.19) становится диагональным:
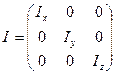 . (16.21)
. (16.21)
16.3. Кинетическая энергия вращающегося тела.
Найдем сначала кинетическую энергию твердого тела, обусловленную его вращательным движением.
С этой целью перейдем в систему центра масс (инерции) и мысленно разобьем тело на маленькие кусочки.
Если угловая скорость 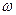 всех точек тела одинакова, можем записать для любого кусочка
всех точек тела одинакова, можем записать для любого кусочка 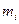 ,
,
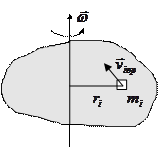 движущегося со скоростью
движущегося со скоростью 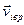 и находящегося на расстоянии
и находящегося на расстоянии 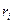 от оси
от оси
вращения:
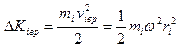
Суммируя по всем кусочкам или, проведя разбиение тела на
элементарные массы 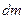 и интегрируя по объему тела, получаем
и интегрируя по объему тела, получаем
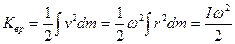 . (16.22)
. (16.22)
16.4. Кинетическая энергия тела при плоском движении.
Несмотря на кажущуюся простоту уравнений (16.2) решение их в общем виде, как уже отмечалось, представляет весьма сложную задачу. Например, разделение кинетической энергии твердого тела, совершающего произвольное движение, на две независимые части, ответственные за поступательное и вращательное движение, возможно лишь в том случае, когда начало подвижной системы координат выбрано в центре инерции тела.
Существенно проще обстоит дело с описанием частного случая движения твердого тела, известного как плоское движение.
Пусть тело совершает в инерциальной 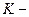 системе, так называемое, плоское движение, т.е. такое, при котором все точки тела движутся параллельно одной плоскости, неподвижной в данной системе отсчета. Другими словами, центр масс тела в течение всего времени движения остается в одной плоскости, и тогда в
системе, так называемое, плоское движение, т.е. такое, при котором все точки тела движутся параллельно одной плоскости, неподвижной в данной системе отсчета. Другими словами, центр масс тела в течение всего времени движения остается в одной плоскости, и тогда в 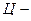 системе тело совершает только вращательное движение вокруг оси, проходящей через центр инерции.
системе тело совершает только вращательное движение вокруг оси, проходящей через центр инерции.
Упрощающим рассмотрение плоского движения обстоятельством служит то, что вектор угловой скорости сохраняет в этом случае свое постоянное направление в пространстве, перпендикулярное плоскости движения, и не изменяет своей ориентации относительно тела.
Энергия поступательного движения тела определяется известной формулой
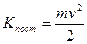 ,
,
где 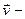 скорость, одинаковая для всех течек тела.
скорость, одинаковая для всех течек тела.
Кинетическую энергию плоского движения твердого тела, одновременно совершающего поступательное и вращательное (относительно оси, проходящей через центр инерции) движение можно представить в виде суммы:
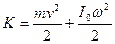 , (16.23)
, (16.23)
где 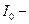 момент инерции тела относительно оси, проходящей через центр инерции.
момент инерции тела относительно оси, проходящей через центр инерции.
Покажем это.
В лабораторной системе отсчета (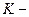 система) имеем
система) имеем
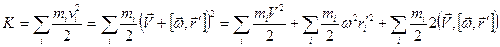
Здесь 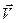 - скорость центра инерции твердого тела (скорость
- скорость центра инерции твердого тела (скорость 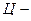 системы).
системы).
Последний член выражения преобразуем с помощью формулы векторной алгебры (циклическая перестановка):
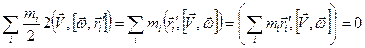
Здесь мы воспользовались тем, что для системы центра инерции 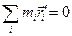 .
.
Таким образом, кинетическая энергия твердого тела при плоском движении складывается из энергии вращения в 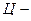 системе и энергии поступательного движения центра инерции (16.23).
системе и энергии поступательного движения центра инерции (16.23).
Пример:
|
Скатывание цилиндра по наклонной плоскости:
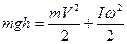
Обратим внимание на формальную аналогию описания поступательного и вращательного движения:
ПоступательноеВращательноеСвязь
Перемещение 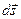
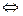 Угол поворота
Угол поворота 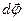
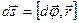
Скорость 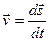
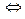 Угловая скорость
Угловая скорость 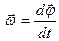
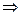
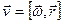
Ускорение 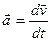
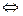 Угловое ускорение
Угловое ускорение 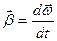
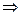
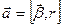
Импульс 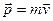
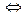 Момент импульса
Момент импульса 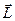
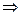
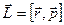
Сила 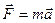
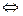 Момент силы
Момент силы 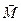

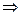
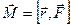
Масса 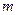
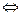 Момент инерции
Момент инерции 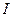
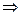
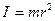
Основное уравнение динамики
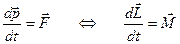 .
.
Демонстрация - скамья Жуковского:
1. Система: вращающаяся скамья + демонстратор, держащий в руках прижатыми к телу гантели (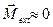 ).
).
При разведении рук с гантелями угловая скорость вращения системы уменьшается, т.к. 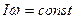
2. Демонстратор, находящийся на неподвижной скамье, держит в руках вращающееся велосипедное колесо.
При изменении направления оси вращения колеса скамья приходит в движение, поскольку сохраняется
момент импульса вдоль оси вращения скамьи.
Углы Эйлера, уравнения Эйлера, гироскопы.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 2594; Нарушение авторских прав?; Мы поможем в написании вашей работы!