Представления стеков

Существует несколько физических представлений стеков:

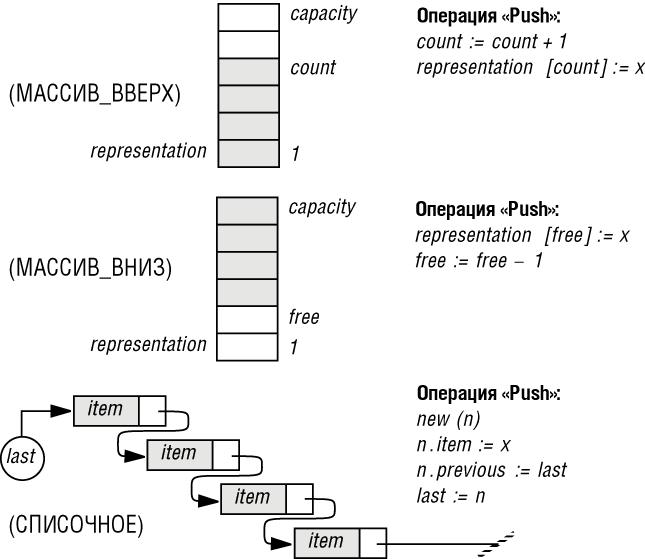
Рис. 6.1. Три возможных представления стеков

Этот рисунок иллюстрирует три наиболее популярных представления стеков. Для удобства ссылок дадим каждому из них свое имя:

• МАССИВ_ВВЕРХ: представляет стек посредством массива representation и целого числа count, с диапазоном значений от 0 (для пустого стека) до capacity - размера массива representation, элементы стека хранятся в массиве и индексируются от 1 до count.
• МАССИВ_ВНИЗ: похож на МАССИВ_ВВЕРХ, но элементы помещаются в конец стека, а не в начало. Здесь число, называемое free, является индексом верхней свободной позиции в стеке или 0, если все позиции в массиве заняты и изменяется в диапазоне от capacity для пустого стека до 0 для заполненного. Элементы стека хранятся в массиве и индексируются от capacity до free +1.
• СПИСОЧНОЕ: при списочном представлении каждый элемент стека хранится в ячейке с двумя полями: item, содержащем сам элемент, и previous, содержащем указатель на ячейку с предыдущим элементом. Для этого представления нужен также указатель last на ячейку, содержащую вершину стека.

Рядом с каждым представлением на рисунке приведен фрагмент программы (в духе Паскаля), с соответствующей реализацией основной стековой операции: втолкнуть элемент x на вершину стека (push).

Для представлений с помощью массивов МАССИВ_ВВЕРХ и МАССИВ_ВНИЗ команды увеличивают или уменьшают указатель на вершину (count или free) и присваивают x соответствующему элементу массива. Так как эти представления поддерживают стеки с не более чем capacity элементами, то корректные реализации должны содержать защищающие от переполнения тесты соответствующего вида:

if count " capacity then...

if free " 0 then...,

(на рисунке они для простоты опущены).

Для представления СПИСОЧНОЕ вталкивание элемента требует четырех действий:

• создания новой ячейки n (здесь оно выполняется с помощью процедуры Паскаля new, которая выделяет память для нового объекта);
• присваивания x полю item новой ячейки;
• присоединения новой ячейки к вершине стека путем присвоения ее полю previous текущего значения указателя last;
• изменения last так, чтобы он ссылался на только что созданную ячейку.

Хотя эти представления встречаются чаще всего, существует и много других представлений стеков. Например, если вам нужны два стека с однотипными элементами и память для их представления ограничена, то можно использовать один массив с двумя метками вершин count как в представлении МАССИВ_ВВЕРХ и free как в МАССИВ_ВНИЗ. При этом один стек будет расти вверх, а другой - вниз. Условием полного заполнения этого представления является равенство count= free.

Преимущество такого представления состоит в уменьшении риска переполнить память: при двух массивах размера n, представляющих стеки способом МАССИВ_ВВЕРХ или МАССИВ_ВНИЗ, память исчерпается, как только любой из стеков достигнет n элементов. А в случае одного массива размера 2n, содержащего два стека лицом к лицу, работа продолжается до тех пор, пока их общая длина не превысит 2n, что менее вероятно, если стеки растут независимо друг от друга. (Для любых переменных p и q, max (p +q) "= max (p) + max (q)).

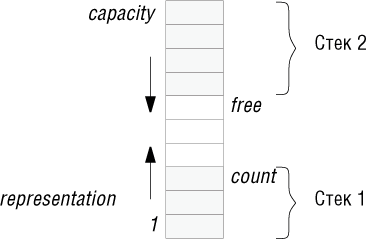
Рис. 6.2. Представление двух стеков лицом к лицу

Каждое из этих и другие возможные представления полезны в разных ситуациях. Выбор одного из них в качестве эталона для определения стека был бы типичным примером излишней спецификации. Почему мы должны, например, предпочесть МАССИВ_ВВЕРХ представлению СПИСОЧНОЕ? Большинство видимых свойств представления МАССИВ_ВВЕРХ - массив, число count, верхняя граница - несущественны для понимания представляемой ими структуры.

Дата добавления: 2014-01-03