Частичные функции

Спецификация всякого реалистичного примера, даже такого простого как стеки, неизбежно сталкивается с проблемами не всюду определенных операций: некоторые операции применимы не ко всем возможным элементам исходных множеств. Например, это имеет место для функций remove и item: нельзя удалить элемент из пустого стека, и у пустого стека нет верхнего элемента.

Решение этой проблемы, использованное в приведенной выше спецификации, состоит в том, чтобы определить эти функции как частичные. Функция из исходного множества X в результирующее множество Y является частичной, если она определена не для всех элементов X. Функция, не являющаяся частичной, называется полной. Простым примером частичной функции в обычной математике является функция обращения действительных чисел inv, значение которой на действительном числе x равно

inv(x)= 1/x.

Поскольку inv не определена при x = 0, мы можем определить ее как частичную функцию на множестве R всех действительных чисел:

Чтобы указать, что функция частичная, используется перечеркнутая стрелка 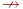, а обычная стрелка 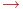будет означать, что функция заведомо полная.

Областью (определения) частичной функции типа 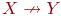является подмножество тех элементов X, для которых эта функция имеет некоторое значение. В нашем примере областью функции inv является R - {0}, т.е. множество действительных чисел, отличных от 0.

В спецификации АТД STACK эти идеи использованы для стеков при объявлении remove и item как частичных функций в разделе ФУНКЦИИ - это указано с помощью перечеркнутых стрелок в их сигнатуре. При этом возникает новая проблема, обсуждаемая в следующем пункте: как задавать области таких функций?

В некоторых случаях функцию put тоже желательно описывать как частичную, например, это требуется в таких реализациях как МАССИВ_ВВЕРХ и МАССИВ_ВНИЗ, которые поддерживают выполнение лишь конечного числа подряд идущих операций put для каждого заданного стека. Это на самом деле полезное упражнение - приспособить спецификацию STACK к тому, чтобы она описывала ограниченные стеки конечного объема, поскольку в приведенном выше виде она не содержит никаких ограничений на размеры стеков.

Это будет новым применением частичных функций, отражающим ограничения реализации. В отличие от этого, объявление функций remove и item как частичных отражает абстрактное свойство этих операций, относящееся ко всем реализациям.

Дата добавления: 2014-01-03