Ничего кроме правды

Сила спецификаций АТД проистекает из их способности отражать только существенные свойства структур данных без лишних деталей. Приведенная выше спецификация стеков выражает все, что нужно по существу знать о понятии стека, и не включает ничего, что относилось бы к каким-либо конкретным реализациям стеков. Это вся правда о стеках, и ничего кроме правды.

Такие спецификации задают общую модель вычислений на соответствующих структурах данных. Определенные в спецификации абстрактного типа данных функции позволяют строить сложные выражения, а аксиомы АТД позволяют упрощать такие выражения и получать более простые результаты. Сложное стековое выражение является математическим эквивалентом программы, а процесс упрощения является математическим эквивалентом вычисления или выполнения этой программы.

Вот пример. Рассмотрим для приведенной выше спецификации АТД STACK следующее выражение stackexp:

item (remove (put (remove (put (put (

remove (put (put (put (new, x1), x2), x3)),

item (remove (put (put (new, x4), x5)))), x6)), x7)))

По-видимому, выражение stackexp будет проще понять, если мы представим его как последовательность вспомогательных выражений:

s1 = new

s2 = put (put (put (s1, x1), x2), x3)

s3 = remove (s2)

s4 = new

s5 = put (put (s4, x4), x5)

s6 = remove (s5)

y1 = item (s6)

s7 = put (s3, y1)

s8 = put (s7, x6)

s9 = remove (s8)

s10 = put (s9, x7)

s11 = remove (s10)

stackexp = item (s11)

Какой бы вариант определения вы ни выбрали, по нему несложно восстановить вычисление, математической моделью которого является stackexp: создать новый стек; втолкнуть в него элементы x1, x2, x3 (в указанном порядке); удалить верхний элемент (x3), назвав получившийся стек s3; создать другой пустой стек и т. д. Этот процесс графически представлен на рис. 6.5.

Можно легко найти значение такого АТД выражения, нарисовав последовательно несколько таких рисунков. (Здесь найдено x4). Но теория позволяет нам получить этот результат формально, не обращаясь к рисункам, а только последовательно применяя аксиомы для упрощения выражения, до тех пор, пока дальнейшее упрощение станет невозможным. Например:

• Применить A2 для упрощения s3 - т. е. заменить remove(put (put (put (s1, x1), x2), x3)) на выражение put (put (s1, x1), x2)). (Согласно A2 всякую пару remove-put можно выбросить).

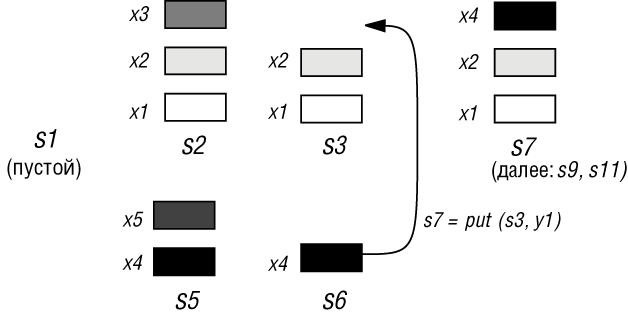
Рис. 6.5. Манипуляции со стеком

• По той же аксиоме s6 равно put(s4, x4). Затем можно применить аксиому A1 и вывести, что y1, т. е. item(put(s4, x4)) на самом деле равно x4, установив тем самым (как указано стрелкой на рисунке), что s7 получается в результате вталкивания x4 на вершину стека s3.

И так далее. Последовательность таких упрощений, выполненная механически так же легко и как последовательность упрощений в элементарной арифметике, приведет к значению выражения stackexp, которое действительно равно x4 (попробуйте проверить это сами, аккуратно проведя весь процесс упрощения).

Этот пример позволяет отметить одну из важнейших теоретических ролей абстрактных типов данных: они предоставляют формальную модель для понятий программы и выполнения программы. Эта модель чисто математическая: в ней нет императивных понятий состояния программы, переменных с изменяемыми во времени значениями, последовательности выполняемых действий. Она основана на обычных математических методах преобразования выражений.

От абстрактных типов данных к классам

Итак, у нас имеется отправная точка - элегантная математическая теория для моделирования структур данных и, как мы только что видели, в целом - программ. Но наша цель - это архитектура ПО, а не математическая или даже теоретическая информатика! Не сбились ли мы с нашего пути? Отнюдь. При поиске подходящей модульной структуры, основанной на типах объектов, АТД предоставляют механизм описания высокого уровня, не связанный с особенностями реализации. Это приведет нас к фундаментальным структурам ОО-технологии.

Классы

В поиске, начатом в лекции 3, АТД будут служить непосредственной основой модулей. Точнее, ОО-система будет строиться (на уровне анализа, проектирования и реализации) как совокупность взаимодействующих, частично или полностью реализованных АТД. Основное понятие здесь - класс:

Определение: класс

Класс - это абстрактный тип данных, снабженный некоторой (возможно частичной) реализацией

Таким образом, чтобы получить класс, мы должны построить АТД и решить, как его реализовывать. АТД - это математическое понятие, а реализация - это его версия, ориентированная на компьютер. Приведенное определение, однако, утверждает, что реализация может быть частичной. Введенные ниже термины позволяют отделить этот случай от полностью реализованного класса:

Определение: отложенный и эффективный классы

Полностью реализованный класс называется эффективным (effective). Класс, который реализован лишь частично или совсем не реализован, называется отложенным (deferred). Всякий класс является либо отложенным, либо эффективным.

Чтобы получить эффективный класс, требуется предусмотреть все детали реализации. Для отложенного класса можно выбрать определенный уровень реализации, но при этом оставить некоторые аспекты реализации незавершенными. В самом крайнем случае при частичной реализации можно вообще отказаться от принятия каких-либо решений о ее уточнении. В этом случае получившийся класс будет полностью отложенным и будет эквивалентен АТД.

Как создавать эффективный класс

Рассмотрим вначале эффективные классы. Что нужно сделать для реализации АТД? Результирующий эффективный класс будет формироваться из элементов трех видов:

• (E1) Спецификации АТД (множество функций с соответствующими аксиомами и предусловиями, описывающими их свойства).
• (E2) Выбора представления.
• (E3) Отображения из множества функций (E1) в представление (E2) в виде множества механизмов (или компонентов (features)), каждый из которых реализует одну из функций в терминах представления и при этом удовлетворяет аксиомам и предусловиям. Многие из этих компонентов будут методами - обычными процедурами, но некоторые могут появляться в качестве полей данных или "атрибутов" (это будет показано в следующих лекциях).

Например, для АТД STACK можно выбрать в качестве представления (шаг E2) решение, названное выше МАССИВ_ВВЕРХ, при котором каждый стек реализуется парой

<representation, count>,

где representation - это массив, а count - это целое число. При реализации функций (E3) у нас будут процедуры для функций put, remove, item, empty и new, выполняющие соответствующие действия. Например, функцию put можно реализовать программой вида

put (x: G)

is -- Втолкнуть x в стек.

-- (без проверки стека на возможное переполнение.)

do

count:= count + 1

representation [count]:= x

end

Объединение элементов, полученных в пунктах (E1), (E2) и (E3), приведет к классу - модульной структуре объектной технологии.

Роль отложенных классов

В определении эффективного класса должна присутствовать полная информация о реализации (пункты E2 и E3). Если она хоть в чем-то неполна, то класс является отложенным.

Чем более "отложенным" является класс, тем он ближе к АТД, одетому в некоторую синтаксическую одежду, которая скорее поможет завоевать признание разработчиков ПО, чем математиков. Отложенные классы особенно полезны при анализе и проектировании:

• При ОО-проектировании многие аспекты реализации будут опущены, проектирование должно сосредотачиваться на архитектурных свойствах высокого уровня - на том, какую функциональность обеспечивает каждый модуль системы, а не на том, как он это делает.
• При постепенном продвижении к полной реализации будут добавляться все новые и новые ее свойства до тех пор, пока не будет получен эффективный класс.

Но на этом роль отложенных классов не завершается, даже в полностью реализованной системе можно часто обнаружить много таких классов. Кое-что следует из только что перечисленных применений: когда из отложенных классов получаются эффективные, то появляется желание сохранить их в качестве предков (в смысле наследования) эффективных классов как живую память о процессе анализа и проектирования.

Очень часто при разработке ПО с помощью не ОО-подходов система в окончательном виде не содержит никаких записей о тех значительных усилиях, которые были затрачены на ее получение. Для тех, кто вынужден будет обслуживать такую систему - расширять, переносить, отлаживать - понять ее без этих записей будет так же трудно, как трудно геологу понять видимый ландшафт, не имея доступа к осадочным слоям. Один из лучших способов обеспечить необходимую для сопровождения системы информацию - это сохранить отложенные классы в ее окончательной форме.

У отложенных классов имеется также применение, полностью связанное с реализацией. Они служат для классификации групп связанных типов объектов, предоставляют некоторые наиболее важные многократно используемые модули высокого уровня, фиксируют общие свойства поведения многих вариантов и играют ключевую роль (вместе с полиморфизмом и динамическим связыванием) в обеспечении децентрализации и расширяемости программной архитектуры.

Несколько следующих лекций, в которых вводятся основные ОО-методы, будут сосредоточены на эффективных классах. Но при этом следует помнить о понятии отложенного класса, чья важность будет расти по мере овладения всей мощью ОО-метода.

Дата добавления: 2014-01-03