
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція 6.Контекстно-свободные грамматики и автоматы с магазинной памятью
|
|
|
|
Пусть G = (N, T, P, S) - КС-грамматика. Введем несколько важных понятий и определений.
Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого левого нетерминала, называется левосторонним. Если S=>* u в процессе левостороннего вывода, то u - левая сентенциальная форма. Аналогично определим правосторонний вывод. Обозначим шаги левого (правого) вывода =>l (=>r).
Упорядоченным графом называется пара (V,E), где V есть множество вершин, а E - множество линейно упорядоченных списков дуг, каждый элемент которого имеет вид ((v, v1), (v, v2),..., (v, vn)). Этот элемент указывает, что из вершины v выходят n дуг, причем первой из них считается дуга, входящая в вершину v1, второй - дуга, входящая в вершину v2, и т.д.
Упорядоченным помеченным деревом называется упорядоченный граф (V,E), основой которого является дерево и для которого определена функция f: V -> F (функция разметки) для некоторого множества F.
Упорядоченное помеченное дерево D называется деревом вывода (или деревом разбора) цепочки w в КС-грамматике G = (N, T, P, S), если выполнены следующие условия:
(1) корень дерева D помечен S;
(2) каждый лист помечен либо 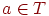 , либо e;
, либо e;
(3) каждая внутренняя вершина помечена нетерминалом 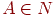 ;
;
(4) если X - нетерминал, которым помечена внутренняя вершина и X1,..., Xn - метки ее прямых потомков в указанном порядке, то X -> X1... Xk - правило из множества P;
(5) Цепочка, составленная из выписанных слева направо меток листьев, равна w.
Процесс определения принадлежности данной строки языку, порождаемому данной грамматикой, и, в случае указанной принадлежности, построение дерева разбора для этой строки, называется синтаксическим анализом. Можно говорить о восстановлении дерева вывода (в частности, правостороннего или левостороннего) для строки, принадлежащей языку. По восстановленному выводу можно строить дерево разбора.
Грамматика G называется неоднозначной, если существует цепочка w, для которой имеется два или более различных деревьев вывода в G.
Грамматика G называется леворекурсивной, если в ней имеется нетерминал A такой, что для некоторой цепочки R существует вывод  .
.
Автомат с магазинной памятью (МП-автомат) - это семерка 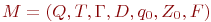 , где
, где
(1) Q - конечное множество состояний, представляющих всевозможные состояния управляющего устройства;
(2) T - конечный входной алфавит;
(3) 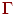 - конечный алфавит магазинных символов;
- конечный алфавит магазинных символов;
(4) D - отображение множества 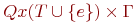 в множество конечных подмножеств
в множество конечных подмножеств 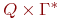 , называемое функцией переходов;
, называемое функцией переходов;
(5) 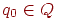 - начальное состояние управляющего устройства;
- начальное состояние управляющего устройства;
(6) 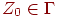 - символ, находящийся в магазине в начальный момент (начальный символ магазина);
- символ, находящийся в магазине в начальный момент (начальный символ магазина);
(7) 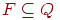 - множество заключительных состояний.
- множество заключительных состояний.
Конфигурация МП-автомата - это тройка (q, w, u), где
(1) 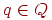 - текущее состояние управляющего устройства;
- текущее состояние управляющего устройства;
(2) 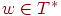 - непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;
- непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;
(3) 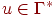 - содержимое магазина; самый левый символ цепочки u считается верхним символом магазина; если u = e, то магазин считается пустым.
- содержимое магазина; самый левый символ цепочки u считается верхним символом магазина; если u = e, то магазин считается пустым.
Такт работы МП-автомата M будем представлять в виде бинарного отношения 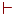 , определенного на конфигурациях.
, определенного на конфигурациях.
Будем писать
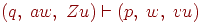
если множество D(q, a, Z) содержит (p, v), где 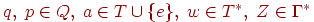 и
и 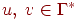 (верхушка магазина слева).
(верхушка магазина слева).
Начальной конфигурацией МП-автомата M называется конфигурация вида (q0, w, Z0), где 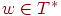 , то есть управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно проанализировать, а в магазине имеется только начальный символ Z0.
, то есть управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно проанализировать, а в магазине имеется только начальный символ Z0.
>Заключительной конфигурацией называется конфигурация вида (q, e, u), где 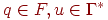 , то есть управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана.
, то есть управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана.
Введем транзитивное и рефлексивно-транзитивное замыкание отношения 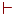 , а также его степень k > 0 (обозначаемые
, а также его степень k > 0 (обозначаемые 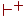 ,
, 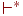 и
и 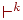 соответственно).
соответственно).
Говорят, что цепочка w допускается МП-автоматом M, если 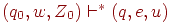 для некоторых
для некоторых 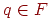 и
и 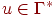 .
.
Множество всех цепочек, допускаемых автоматом M называется языком, допускаемым (распознаваемым, определяемым) автоматом M (обозначается L(M)).
Пример 4.1. Рассмотрим МП-автомат
M = ({q0, q1, q2}, {a, b}, {Z, a, b}, D, q0, Z, {q2}),
у которого функция переходов D содержит элементы:
D(q0, a, Z) = {(q0, aZ)},D(q0, b, Z) = {(q0, bZ)},D(q0, a, a) = {(q0, aa), {q1, e)},D(q0, a, b) = {(q0, ab)},D(q0, b, a) = {(q0, ba)},D(q0, b, b) = {(q0, bb), (q1, e)},D(q1, a, a) = {(q1, e)},D(q1, b, b) = {(q1, e)},D(q1, e, Z) = {(q2, e)}.Нетрудно показать, что 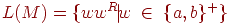 , где wR обозначает обращение ("переворачивание") цепочки w.
, где wR обозначает обращение ("переворачивание") цепочки w.
Иногда допустимость определяют несколько иначе: цепочка w допускается МП-автоматом M, если 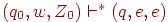 для некоторого
для некоторого 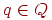 . В таком случае говорят, что автомат допускает цепочку опустошением магазина. Эти определения эквивалентны, ибо справедлива
. В таком случае говорят, что автомат допускает цепочку опустошением магазина. Эти определения эквивалентны, ибо справедлива
Теорема 4.1. Язык допускается МП-автоматом тогда и только тогда, когда он допускается (некоторым другим автоматом) опустошением магазина.
Доказательство. Пусть L = L(M) для некоторого МП- автомата 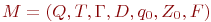 . Построим новый МП- автомат M', допускающий тот же язык опустошением магазина.
. Построим новый МП- автомат M', допускающий тот же язык опустошением магазина.
Пусть 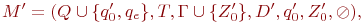 где функция переходов D' определена следующим образом:
где функция переходов D' определена следующим образом:
- Если
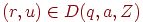 , то
, то 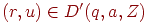 для всех
для всех 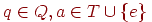 и
и 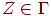 (моделирование М),
(моделирование М), 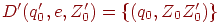 (начало работы),
(начало работы), - Для всех
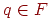 и
и 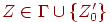 множество D'(q, e, Z) содержит (qe, e) (переход в состояние сокращения магазина без продвижения),
множество D'(q, e, Z) содержит (qe, e) (переход в состояние сокращения магазина без продвижения), - D'(qe, e, Z) = {(qe, e)} для всех
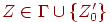 , (сокращение магазина).
, (сокращение магазина).
Автомат сначала переходит в конфигурацию 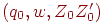 соответственно определению D' в п.2, затем в
соответственно определению D' в п.2, затем в 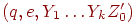 ,
,
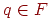 соответственно п.1, затем в
соответственно п.1, затем в 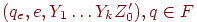 соответственно п.3, затем в (qe, e, e) соответственно п.4. Нетрудно показать по индукции, что
соответственно п.3, затем в (qe, e, e) соответственно п.4. Нетрудно показать по индукции, что 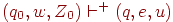 (где
(где 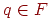 ) выполняется для автомата M тогда и только тогда, когда
) выполняется для автомата M тогда и только тогда, когда 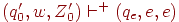 выполняется для автомата M'. Поэтому L(M) = L', где L' - язык, допускаемый автоматом M' опустошением магазина.
выполняется для автомата M'. Поэтому L(M) = L', где L' - язык, допускаемый автоматом M' опустошением магазина.
Обратно, пусть 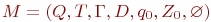 - МП - автомат, допускающий опустошением магазина язык L. Построим автомат M', допускающий тот же язык по заключительному состоянию.
- МП - автомат, допускающий опустошением магазина язык L. Построим автомат M', допускающий тот же язык по заключительному состоянию.
Пусть 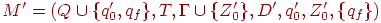 , где D' определяется следующим образом:
, где D' определяется следующим образом:
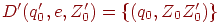 - переход в "режим M ",
- переход в "режим M ", - Для каждого
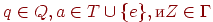 определим
определим 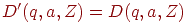 - работа в "режиме M ",
- работа в "режиме M ", - Для всех
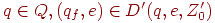 - переход в заключительное состояние.
- переход в заключительное состояние.
Нетрудно показать по индукции, что L = L(M'). Одним из важнейших результатов теории контекстно-свободных языков является доказательство эквивалентности МП-автоматов и КС-грамматик.
Теорема 4.2. Язык является контекстно-свободным тогда и только тогда, когда он допускается МП-авто- матом.
Доказательство.(алгоритм побудови мп-автомату по КВ граматиці). Пусть G = (N, T, P, S) - КС-граммати- ка. Построим МП-автомат, допускающий язык L(G) опустошением магазина.
Пусть 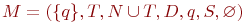 , где D определяется следующим образом:
, где D определяется следующим образом:
- Если
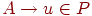 , то
, то 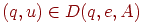 ,
, - D(q, a, a) = {(q, e)} для всех
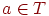 .
.
Фактически, этот МП-автомат в точности моделирует все возможные выводы в грамматике G. Нетрудно показать по индукции, что для любой цепочки 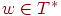 вывод S =>+w в грамматике G существует тогда и только тогда, когда существует последовательность тактов
вывод S =>+w в грамматике G существует тогда и только тогда, когда существует последовательность тактов  автомата M.
автомата M.
Алгоритм побудови Кв граматики по мп-автомату)
Наоборот, пусть дан 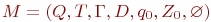 - МП- автомат, допускающий опустошением магазина язык L.
- МП- автомат, допускающий опустошением магазина язык L.
Построим грамматику G, порождающую язык L.
Пусть 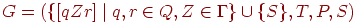 , где P состоит из правил следующего вида:
, где P состоит из правил следующего вида:
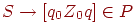 для всех
для всех 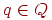 .
. - Если
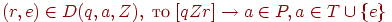 ,
, - Если
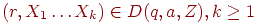 , то
, то
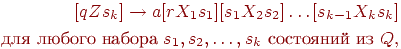
Нетерминалы и правила вывода грамматики определены так, что работе автомата M при обработке цепочки w соответствует левосторонний вывод w в грамматике G.
Индукцией по числу шагов вывода в G или числу тактов M нетрудно показать, что 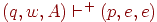 тогда и только тогда, когда [qAp] =>+ w.
тогда и только тогда, когда [qAp] =>+ w.
Тогда, если 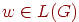 , то S => [q0Z0q] =>+ w для некоторого
, то S => [q0Z0q] =>+ w для некоторого 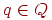 . Следовательно,
. Следовательно, 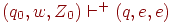 и поэтому
и поэтому 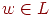 . Аналогично, если
. Аналогично, если 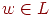 , то
, то 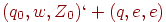 . Значит, S =>[q0Z0q] =>+ w, и поэтому
. Значит, S =>[q0Z0q] =>+ w, и поэтому 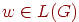 .
.
|
|
|
Дата добавления: 2014-01-03; Просмотров: 665; Нарушение авторских прав?; Мы поможем в написании вашей работы!